Требования к выполнению контрольных и лабораторных работ

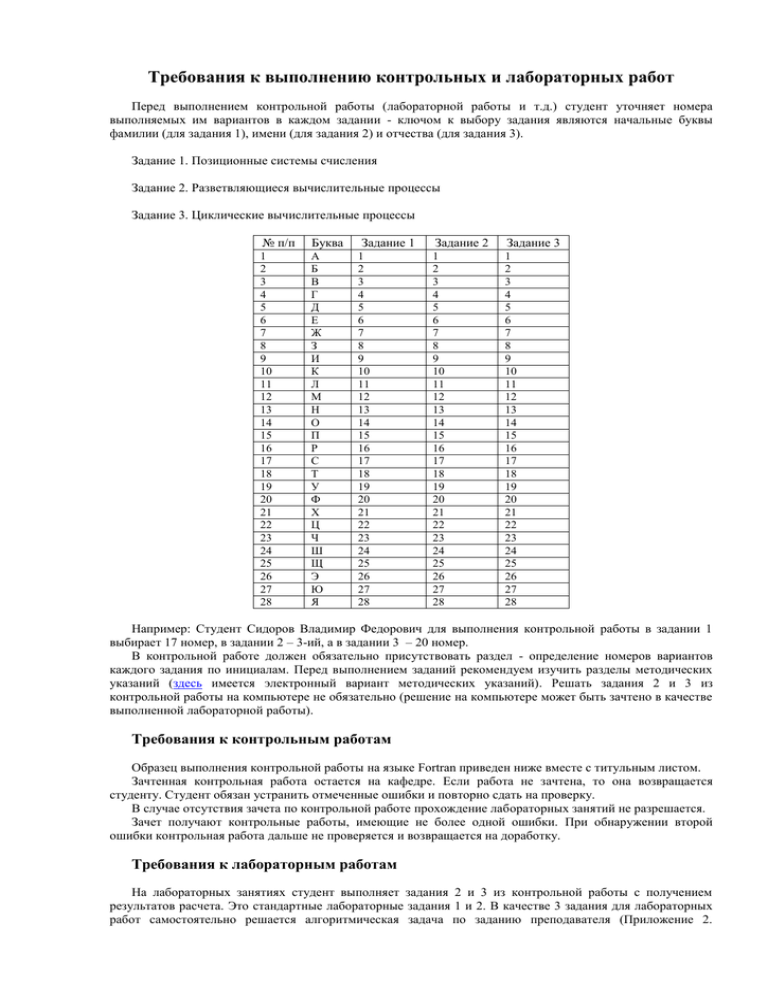
Требования к выполнению контрольных и лабораторных работ
Перед выполнением контрольной работы (лабораторной работы и т.д.) студент уточняет номера
выполняемых им вариантов в каждом задании - ключом к выбору задания являются начальные буквы
фамилии (для задания 1), имени (для задания 2) и отчества (для задания 3).
Задание 1. Позиционные системы счисления
Задание 2. Разветвляющиеся вычислительные процессы
Задание 3. Циклические вычислительные процессы
№ п/п
Буква
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Э
Ю
Я
Задание 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Задание 2
Задание 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Например: Студент Сидоров Владимир Федорович для выполнения контрольной работы в задании 1
выбирает 17 номер, в задании 2 – 3-ий, а в задании 3 – 20 номер.
В контрольной работе должен обязательно присутствовать раздел - определение номеров вариантов
каждого задания по инициалам. Перед выполнением заданий рекомендуем изучить разделы методических
указаний (здесь имеется электронный вариант методических указаний). Решать задания 2 и 3 из
контрольной работы на компьютере не обязательно (решение на компьютере может быть зачтено в качестве
выполненной лабораторной работы).
Требования к контрольным работам
Образец выполнения контрольной работы на языке Fortran приведен ниже вместе с титульным листом.
Зачтенная контрольная работа остается на кафедре. Если работа не зачтена, то она возвращается
студенту. Студент обязан устранить отмеченные ошибки и повторно сдать на проверку.
В случае отсутствия зачета по контрольной работе прохождение лабораторных занятий не разрешается.
Зачет получают контрольные работы, имеющие не более одной ошибки. При обнаружении второй
ошибки контрольная работа дальше не проверяется и возвращается на доработку.
Требования к лабораторным работам
На лабораторных занятиях студент выполняет задания 2 и 3 из контрольной работы с получением
результатов расчета. Это стандартные лабораторные задания 1 и 2. В качестве 3 задания для лабораторных
работ самостоятельно решается алгоритмическая задача по заданию преподавателя (Приложение 2.
Методических указаний по выполнению контрольных работ “Информатика” авторы В.И. Логинов, Л.Н.
Шемагина). Электронный вариант этих методических указаний можно взять здесь. Перед выполнение
лабораторной работы студент защищает схему алгоритма и текст программы, затем вводит программу в
компьютер, отлаживает и получает решение задачи. Перед выполнением задачи на компьютере во время
защиты лабораторной работы студент должен определить входные данные для тестирования программы и
вручную просчитать результат выполнения задачи на этих тестовых данных. Отчеты по лабораторным
работам содержат те же сведения, что и в контрольной работе при выполнении задания 2 и 3, но добавляется
пункт результаты решения задачи на компьютере (на тестовых и (или) других входных данных).
Если студент не смог сдать теоретический коллоквиум и защитить схему решения задачи, то он не
допускается для работы на компьютере.
Отчет оформляется в печатном или письменном виде.
Пример выполнения контрольной работы
Федеральное агентство морского и речного транспорта
Федеральное государственное образовательное учреждение
высшего профессионального образования
“Волжская государственная академия водного транспорта”
(ФГОУ ВПО “ВГАВТ”)
Кафедра Информатики систем управления и телекоммуникаций
Информатика
Контрольная работа
Электромеханический факультет
Заочная форма обучения
1 курс
Выполнил: ст. группы М-125
Петров И. С.
Проверил: _______________
Н. Новгород
2007 г.
Студент Петров Иван Степанович
По первым буквам фамилии (П), имени (И) и отчества (С) выбираем номера вариантов заданий из
таблицы методических указаний, представленной в п. 1. По первой букве фамилии П из таблицы выбираем
задание 1 “Позиционные системы счисления” – вариант 15, по первой букве имени И выбираем задание 2
“Разветвляющиеся вычислительные процессы” – вариант 9, по первой букве отчества С для задания 3
“Циклические вычислительные процессы” – вариант 17.
Задание 1. Позиционные системы счисления.
Вариант 15.
Представить числа в четырех системах счисления 10-ой, 2-ой, 8-ой и 16-ой:
№ варианта
Целые числа
Действительные числа
15
22010 ,
5208 ,
101011012 , 12716
15,312510 , 171,258 ,
1101011,110012 , 15,2116
Представить (перевести) целые числа в четырёх системах счисления 10-ой, 2-ой, 8-ой, и 16-ой:
22010 ,
5208 ,
101011012 ,
12716
1. Перевод десятичного числа 22010
Перевод в двоичную систему счисления:
Ответ: 22010 = 110111002
Перевод в 8-ю систему. Разбиваем на триады: 11 011 100. Дополняем старшую триаду нулем и
заменяем триады восьмеричными цифрами.
Ответ: 22010 = 3348
Перевод в 16-ю систему. Разбиваем двоичное число на тетрады: 1101
1100. Заменяем
соответствующими шестнадцатеричными цифрами.
Ответ: 22010 = DC16
2. Перевод восьмеричного числа 5208
Перевод в 10-ю систему.
5208 = 5*82 + 2*81 + 0*80 = 33610
Перевод в 2-ю систему. Каждое восьмеричное число преобразуем в двоичное раздельно (триадами)
5208 = 101 010 0002
Перевод в 16-ю систему. Число, полученное при переводе в двоичную систему, разбиваем на тетрады и
заменяем их 16-ными цифрами в соответствии с известной таблицей.
101 010 0002 = 1 0101 000 = 0001 0101 0000
Ответ: 5208 = 15016
3. Перевод двоичного числа 101011012.
Перевод в 10-ю систему
101011012 =1*27 + 0*26 + 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 17310
Перевод в 8-ю систему (триадами).
10 101 1012 = 2558
Перевод в 16-ю систему (тетрадами).
1100 11012 =АD16
4. Перевод шестнадцатеричного числа 12716
Перевод в 10-ю систему
12716 = 1*162 + 2*161 + 7*160 = 29510
Перевод в 2-ю систему (тетрадами).
12716 = 0001 0010 01112 = 100 100 1112
Перевод в восьмеричную систему.
12716 = 100 100 1112 = 4478
Представить (перевести) действительные числа в четырёх системах счисления 10-ой, 2-ой, 8-ой, и 16-ой :
15,312510 , 171,258 , 1101011,110012 , 15,2116
5. Перевод десятичного действительного числа 15,312510
Перевод в 2-ю систему счисления.
Перевод десятичных цифр, целых и дробных, в другую позиционную систему проводится по разным
правилам. Поэтому отдельно переведём целую и дробную часть
Ответ: 15,312510 = 1111,01012
Перевод в 8-ю систему. Разбиваем полученное двоичное число на триады влево и право от запятой:
1 111, 010 1. Крайние триады оказались не полными, дополняем их нулями: 001 111, 010 100: Заменяем
триады восьмеричными цифрами
Ответ: 15,312510 = 17,248
Перевод в 16-ю систему. Разбиваем двоичное число на тетрады; влево и вправо от запятой: 1111, 0101.
Заменяем тетрады шестнадцатеричными цифрами
Ответ: 15,312510 =F,516
6. Перевод восьмеричного действительного числа: 171,258
Перевод в 10-ю систему (с учетом только 4 цифр после десятичной запятой).
171,258  1  8 2  7  81  1  8 0 
2 5
21

 121
 121,3281
8 82
6410
Перевод в 2-ю систему.
171,258 =1 111 001, 010 1012
Перевод в 16-ю систему. Полученное выше двоичное число разбиваем на тетрады влево и вправо от
запятой получим.
171,258 = 79,5416
7. Перевод двоичного действительного числа: 1101011, 110012
Перевод в 10-ю систему.
1101011,110012  1  2 6  1  2 5  0  2 4  1  2 3  0  2 2  1  21  1  2 0 

1 1
0
0
1
25
 2  3  4  5  107
 107,7812510
2 2
32 10
2
2
2
Перевод в 8-ю систему. Разбиваем на триады и получаем
1 101 011, 110 012 =153,628
Перевод в 16-ю систему. Разбиваем на тетрады и получаем.
110 1011, 1100 12=6В,С816
8. Перевод шестнадцатеричного действительного числа: 15,2116
Перевод в 10-ю систему (с точностью до 4-х знаков).
15,2116  1  161  5  16 0 
2
1
33
 2  21
 21,128910
16 16
256 10
Перевод в 2-ю систему.
15,2116 = 1 0101, 0010 00012
Перевод в 8-ю систему.
15,2116 = 10 101, 001 000 012 = 25,1028
Задание 2. Разветвляющиеся вычислительные процессы.
Вариант 9.
Вычислить выражение
Z = max(A2+B, min (B+1, C))
Составить схему разветвляющегося вычислительного процесса и написать программу на любом
алгоритмическом языке.
Решение
В данном примере возможны три варианта ответа: или A2+B, или B+1, или С. Выбор будет выполнен
только по результатам проверки условий.
Введем промежуточную переменную R и следующие обозначения:
R= min(B+1,C), тогда
Z=max(A2+B, R)
Алгоритм вычисления будет иметь вид:
С , если B  1  C
R
B  1, если B  1  C
 A 2  B , если A 2  B  R
Z 
 R , если A 2  B  R
Схема вычисления будет содержать следующие символы действий:
- Начало и Останов;
- Ввод данных A,B,C;
- Два символа Решения, проверяющих условия B+1>=C? и A2+B>=R?;
- Четыре символа Процесс, которые присваивают переменным R и Z определенное значение;
- Документ (Вывод значения Z).
Схема представлена на рисунке ниже.
Составим программу вычисления Z на алгоритмическом языке Fortran-90.
Исходные данные – переменные вещественного типа в естественной форме A, B, C. Все типы
переменные в программе определяются по соглашению (по умолчанию - неявным способом).
Схема вычисления Z = max(A2+B, min (B+1, C))
Для ввода исходных данных и вывода результата используем ввод и вывод под управлением списка.
Исходные данные A, B, C будем вводить с клавиатуры, а результат Z выведем на дисплей.
Для вычисления переменной R и результата Z используем структурный логический оператор IF.
*
*
*
*
*
Вычисление Z = max(A2+B,min(B+1,C))
Ввод исходных данных А,В, C
READ (*,*) A,B,C
Вычисление R = min(B+1,C)
IF ( B+1 < C) THEN
R = B+1
ELSE
R=C
ENDIF
Вычисление Z = max(A2+B,R)
IF(A**2+B >= R) THEN
Z = A**2+B
ELSE
Z=R
ENDIF
Печать результата
WRITE(*,*) ' Z= ',Z
END
Задание 3. Циклические вычислительные процессы.
Вариант 17.
Даны массивы Ai , i=1,…,10 и Bj , j=1,…,15. Найти максимальные элементы массивов Amin и Bmin.
Определить, какой из Amin или Bmin больше по абсолютной величине.
Составить схему вычислительного процесса и программу на любом алгоритмическом языке. Входные
данные задать самостоятельно.
Решение
Нахождение минимального элемента массива A выполняется в цикле путем сравнения текущего
элемента массива с минимальным из всех предыдущих. Для выбора внутри цикла используется следующая
формула
 Ai , если Ai  Amin
Amin  
 Amin , если Ai  Amin .
Перед началом цикла задается начальное значение Amin=A1, и поиск в цикле начинается со второго
элемента.
Аналогично вычисляется и Bmin.
Схема будет содержать два цикла: первый по параметру i от 2 до 10 с шагом 1, второй по параметру j от
2 до 15 с шагом 1. В результате работы первого цикла будет вычислен Amin, в результате работы второго Bmin. Схема вычислений приведена на рисунке ниже.
Составим программу вычисления на алгоритмическом языке Fortran-90.
Исходные данные – массивы Ai , i=1,…,10. и Bj , j=1,…,15 состоят из переменных вещественного тип,
значения которых зададим самостоятельно. Первым оператором программы будет оператор DIMENSION,
который объявит массивы и укажет их максимальный размер.
Для ввода исходных данных (общее количество элементов массивов равно 25) используем
невыполняемый оператор DATA. Результаты выведем на дисплей под управлением списка.
Циклы организуем с помощью структурного оператора цикла. Для выбора минимальных элементов
внутри циклов Amin и Bmin и сравнения их по абсолютной величине используем логический оператор IF.
Схема вычисления Amin , Bmin и анализ их значений по абсолютной величине.
Текст программы на алгоритмическом языке Fortran
* Поиск минимальных элементов в массивах A, B и их сравнение
*
по абсолютной величине
DIMENSION A(10),B(15)
* Ввод массивов
DATA A/-20.42,-11.80,-19.90,44.86,47.98,-9.86,-22.17,
* -33.96,-33.72,14.66,/,
* B/-13.50,-1.01,-34.43,-2.55,-24.27,12.88,
* 4.21,-34.37,43.85,15.45,0.61,-10.95,-39.26,28.40,-4.04/
* Задание начальных значений
Amin = A(1)
Bmin = B(1)
* Организация цикла по параметру I.
DO I = 2,10
*
Выбор минимального элементов массива A и сохранение в Amin
IF(A(I) < Amin )THEN
Amin = A(I)
ENDIF
ENDDO
*
Организация цикла по параметру J.
DO J = 2,15
*
Выбор минимального элементов массива B и сохранение в Bmin
IF(B(J) < Bmin)THEN
Bmin = B(J)
ENDIF
ENDDO
*
Печать Amin и Bmin
WRITE(*,*)’ Amin=’,Amin,’ Bmin=’,Bmin
*
Сравнение |Amin| и |Bmin|
IF(ABS(Amin) > = ABS(Bmin))THEN
WRITE(*,*)’ |Amin| больше или равен |Вmin|’
ELSE
WRITE(*,*)’ |Bmin| больше |Amin|’
ENDIF
END