Документ 604450

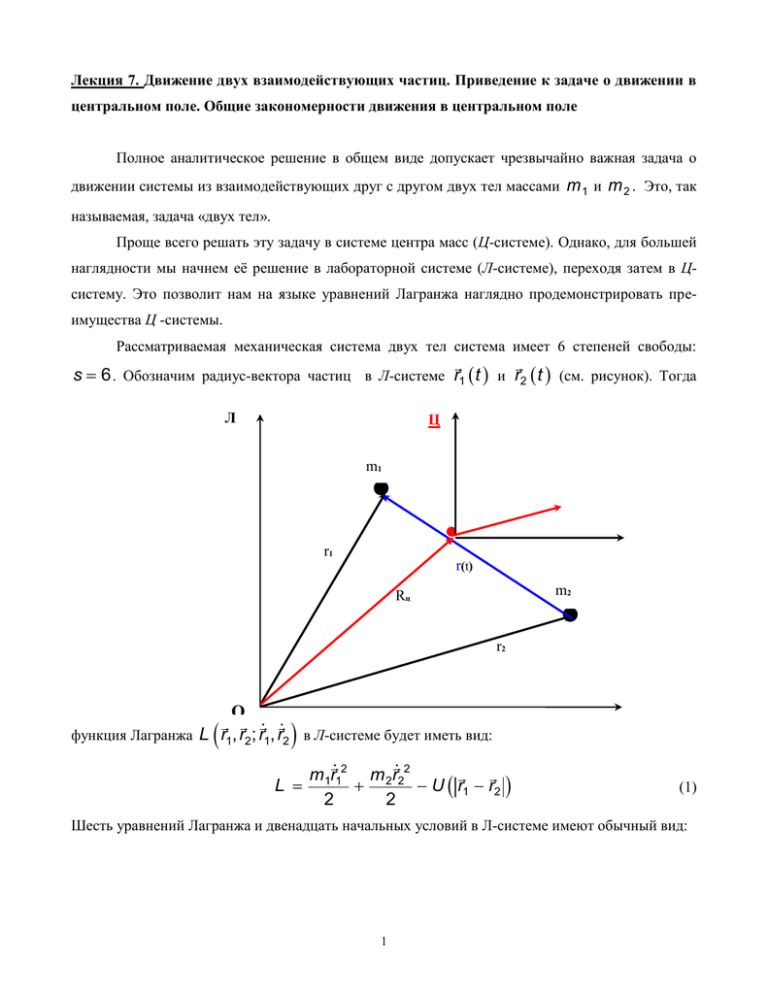
Лекция 7. Движение двух взаимодействующих частиц. Приведение к задаче о движении в
центральном поле. Общие закономерности движения в центральном поле
Полное аналитическое решение в общем виде допускает чрезвычайно важная задача о
движении системы из взаимодействующих друг с другом двух тел массами m 1 и m 2 . Это, так
называемая, задача «двух тел».
Проще всего решать эту задачу в системе центра масс (Ц-системе). Однако, для большей
наглядности мы начнем её решение в лабораторной системе (Л-системе), переходя затем в Цсистему. Это позволит нам на языке уравнений Лагранжа наглядно продемонстрировать преимущества Ц -системы.
Рассматриваемая механическая система двух тел система имеет 6 степеней свободы:
s  6 . Обозначим радиус-вектора частиц в Л-системе r1  t  и r2  t  (см. рисунок). Тогда
Л
Ц
.
m1
V
.
r1
ц
.
r(t)
m2
Rц
r2
O
функция Лагранжа L r1, r2; r1, r2 в Л-системе будет иметь вид:


L 
m1r12 m 2r22

 U  r1  r2 
2
2
(1)
Шесть уравнений Лагранжа и двенадцать начальных условий в Л-системе имеют обычный вид:
1







d
dt
 L  L
;



r

r
1
 1
d
dt
 L  L
;


 r2  r2
 r1  t  0  r10 ;

 r2  t  0  r20 ;
r1  t  0  v10 ;
r2  t  0  v20 ;
(2)
P0  m1v10  m2v20
(3)
Т.к. система замкнута, что её полный импульс сохраняется:
P  t   m1r1  t   m2r2  t   P0 ;
где
Ц
Поскольку потенциальная энергия взаимо-
.
действия частиц зависит только от расстоя-
m1
ния r1  r2 между частицами, то с учетом
формулы (3), удобно от пары векторных
Vц(t)
r1ц
переменных r1  t  и r2  t  перейти к но-
.
r2ц
r(t)
вым переменным R  t  и r  t  (См. рисунок):
R t  
.
m2
m1r1  m 2r2
m1  m 2
и
r  t   r1  r2
(4)
Из формул (4) находим связь между старыми и новыми переменными:
m2

 r1  t   R  t   m  m r  t  ;
1
2

m1
 r2  t   R  t  
r t  ;
m1  m 2

(5)
Величина R  t  есть не что иное, как центр инерции системы: R  t   Rö  t  . Величина r  t 
определяет относительное расположение частиц друг относительно друга.
В
Ц
-системе,
радиус-вектор
каждой
из
r2ц  t   r2  t   R t  будет определяться по формулам:
2
частиц
r1ц  t   r1  t   R  t 
и
m2

r
t

r t ;


1
ц

m

m

1
2

r  t    m1 r  t  ;
 2ц
m1  m2
(6)
Переход к новым переменным, фактически, представляет движение механической системы из
двух тел как движение её как целое (переменная R  t  ) и движение каждой из частиц относительно их общего центра инерции (переменные r1ц  t  и r2ц  t  ).
Дифференцируя уравнения (5) по времени и подставляя полученные производные в выражение для функции Лагранжа системы (1), получим

L r , R, r , R

m1  m2  R 2 r 2



U
2
2
r 
(7)
где введено обозначение

m1m2
m1  m2
(9)
Величина  (9) называется приведенной массой двух тел. Функция Лагранжа (7) в новых переменных состоит из двух слагаемых: первое зависит только от величины R , причем радиус вектор центра инерции R(t ) является циклической переменной. Второе слагаемое зависит только
от величин r и r , и только в него входит потенциальная энергия взаимодействия U  r  . Но
это означает, что в новых переменных уравнения Лагранжа для величин R(t ) и r  t  будут независимыми – закон относительного движения частиц r  t  никак не связан с движением центра инерции системы R(t ) .
Из формулы (7) получаем уравнения Лагранжа системы двух тел
 m1  m2  R  0;
r  
U (r )
r
(10)
Уравнения (10) означают, что, во-первых, центр инерции системы движется равномерно и прямолинейно, а, во вторых, относительное движение тел таково, каким было бы движение тела с
приведенной массой в потенциале U  r  .
3
Таким образом, для того чтобы определить положение каждой из двух частиц, как в Лсистеме, так и в Ц-системе, остается определить зависимость от времени только их относительного движения, т.е. величины r  t  .
Таким образом, переход в Ц – системе позволяет задачу с шестью степенями свободы,
свести к более простой задаче с тремя степенями свободы. Поэтому следующий шаг состоит в
том, чтобы получить уравнение непосредственно для величины r  t  . Поэтому становится актуальной проблема изучения движения одной м. точки в заданном внешнем Ц.С. поле U  r  .
Эта задача в общем виде будет рассматриваться в следующей лекции; сейчас же в связи со вторым уравнением (10) рассмотрим вопрос о силах, которые действуют на частицу в центральносимметричном поле.
Если потенциальная энергия частицы U(r ) зависит только от расстояния r до определенной неподвижной точки, которая называется центром поля, то на частицу со стороны поля
действует сила
F r   
U  r 
dU  r  r


r
dr
r
(11)
Эта сила по абсолютной величине зависит только от расстояния до центра поля r и направлена
в каждой точке r коллинеарною радиус-вектору r . Если
сила отталкивания
 F  r  .
 F  r  . Если
dU  r 
 0 , то в данной точке это
dr
dU  r 
 0 , то в данной точке это сила притяжения
dr
Важнейшими ЦС полями являются: гравитационное поле двух точечных масс
m1, m 2 (закон всемирного тяготения Ньютона) и электростатическое поле двух точечных зарядов q1, q2 (закон Кулона):
U грав  r   
m1  m2
;
r
Fграв  r   
m1  m2 r
;
r2 r
U кул  r   
q1  q2
.
r
Fкул  r   
q1  q2 r
.
r2 r
Гравитационное поле может быть только полем притяжения  m1  m 2  0 . Кулоновское поле
может быть как полем притяжения  q1  q2  0 так и полем отталкивания  q1  q2  0 , при-
4
чем первый случай реализуется при разноименных зарядах движущейся частицы и центра поля,
второй – в случае, когда эти заряды одноименные.
5