Пример семестрового («большого») домашнего задания По курсу «Аналитическая механика»

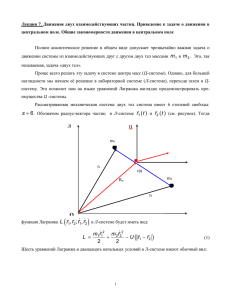
Пример семестрового («большого») домашнего задания
По курсу «Аналитическая механика»
(для всех групп факультета
Экспериментальной и теоретической физики МИФИ)
Задача 1. Написать функцию Лагранжа и уравнения Лагранжа для двойного математического маятника.
Задача 2. Гладкий стержень может вращаться в горизонтальной плоскости XoY
    Const.
вокруг вертикальной оси OZ с постоянной угловой скоростью 
Вдоль стержня может скользить без трения тело m . В начальный момент времени
t  0 стержень располагался вдоль оси OX , а тело m находилось на расстоянии 0
от оси вращения и покоилось. Определить закон движения тела после того, когда
стержень начнет вращаться. На каком расстоянии будет находиться тело, после того,
когда стержень сделает один полный оборот?
Задача 3. Тело M прикреплено к пружине
y
M
жесткостью k и может двигаться без трения
в горизонтальном направлении (вдоль оси
Ox ). Маятник длиной l и массы m при-
x
x t 
l0
t  l
креплен к массе M и может колебаться в
вертикальной плоскости
x2
XoY . Написать
функцию Лагранжа и уравнения Лагранжа
y2
m
для этой механической системы (см. рисунок).
Задача 4. Вычислить период колебаний плоского математического маятника длиной
l в зависимости от амплитуды колебаний  m . Из точной формулы получить при-
ближенную формулу для периода малых колебаний, когда  m
1
1.
Задача 5. Определить закон движения x t  ча-
y
стицы массы m в потенциальном поле притяжения Ux   Ax 4
A  0 ,
полная энергия
E  E0  0 . В начальный момент времени ча-
O

v0
x0

v0
m
x
стица находилась в точке x t  0  x 0  0 (См.
рисунок). Рассмотреть два случая: начальная скорость v0x  v0  0 и v 0x   v 0  0 .
В каких случаях движение будет финитным или инфинитным?

 
Задача 6. Доказать, что проекция полного момента импульса M  [r , p] одной м.
точки на любую ось (назовем её осью z ), может быть определена по формуле:
M z  L / 
Здесь  есть угол поворота вокруг этой оси, а L - функция Лагранжа в полярных
координатах.

Задача 7. Получить формулы преобразования полного импульса P и полной механической энергии системы E из N материальных точек при переходе из лабораторной системы отсчета K в любую другую инерциальную систему отсчета K  . Отдельно рассмотреть случай, когда система K  является системой центра инерции.
Задача 8. Частица совершает одномерное движение в поле U  x   U0 / ch 2 ( x / a) ,
U 0  0 . Найти период финитного движения. Нарисовать фазовые траектории части-
цы. Какой вид имеет фазовая траектория при E  0 ?
Задача 9. Вычислить время падения частицы m на центр поля притяжения
Ur     / r 2 , если в начальный момент времени тело находилось на расстоянии
r t  0  r0 и покоилось: v t  0  0 .
Задача 10. Тело m находится в центрально симметричном поле притяжения
U r     / r . Построить график зависимости «эффективной» потенциальной энер2

гии Ueff r  при заданном значении полного момента импульса M  M 0 , включая
случай M 0  0 . На каком расстоянии r от центра поля, величина Ueff r  имеет минимальное значение Ueff
min
и чему оно равно? При каких энергиях частицы E
движение будет инфинитным или финитным. Определить расстояние от центра поля
до точек поворота в зависимости от энергии частицы E . При какой энергии E движение будет происходить по окружности и чему равен радиус этой окружности?
Задача 11. Найти эффективное сечение падения на центр в поле U(r) =  / (r + a)r2.
Исследовать предельные случаи малых и больших энергий.
Задача 12. Определить дифференциальное и полное сечение рассеяния частицы m 1
на абсолютно твердом шарике радиуса a и массы m 2  m 1 . Потенциальная энергия взаимодействия определяется выражением:
, если r  a,
Ur   
0, если r  a
3