Конспект урока по теме: "Задачи на построение сечений". 10-й
реклама

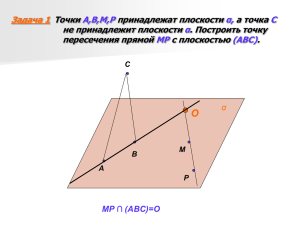
Конспект урока по теме: "Задачи на построение сечений". 10-й класс. Геометрия с применением "презентации" Цели урока: сформировать навык решения простейших задач на построение; развитие пространственного воображения; развитие логического мышления; проверка знаний теоретического материала. Ход урока I. Актуализация знаний, необходимых на уроке. Двое учащихся у доски выполняют задание, подобное домашней работе. Задание 1. Рисунок 1 Дано: А ; М ; Р ; С ; В . Построить точку пересечения прямой МР с плоскостью (АВС). Задание 2. Рисунок 2 Дано: Е ; F ; М . Построить линии пересечения плоскости (EFM) с плоскостями и . Остальные работают устно (слайд 1). 1. Верно ли утверждение: а) плоскости (АВС) и (А' В' С') параллельны; б) прямые А'В' и СD параллельны; в) прямые А'' В''и D'С'параллельны; г) точка В' принадлежит плоскости А'СD; д) плоскости (А''В''С'), (А'В'С') и (АВС) пересекаются по одной прямой ; е) плоскости (А''В''С'') и (DСА') пересекаются по прямой, параллельной прямой CD. 2. Укажите: а) прямую пересечения плоскостей (А'В'С') и (СDD'); б) прямую пересечения плоскостей (D'OD) и (АВС); в) точку пересечения плоскости АDС и прямой В'В; г) точку пересечения плоскости (ВВ'D') и прямой СD. II. Изучение нового материала. 1. Введение понятия секущей плоскости и сечения (слайд 2). 2. Работа по рисункам (рисунок 3 нарисован заранее с обратной стороны доски) и модели куба. Учитель. Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли? Сделайте вывод, как построить сечение в кубе? Рисунок 3 Первые три рисунка учитель показывает на доске, последние два ученики выполняют в тетрадях самостоятельно. Формулируются выводы – правила для построения сечений: 1. Для построения сечения достаточно построить точки пересечения секущей плоскости с рёбрами куба (тетраэдра, параллелепипеда). 2. Через полученные точки, лежащие в одной грани, провести отрезки. 3. Многоугольник, ограниченный данными отрезками, и есть построенное сечение. 4. Если секущая плоскость пересекает противоположные грани куба (параллелепипеда) по каким-либо отрезкам, то эти отрезки параллельны. 3. Применяя полученные выводы, построить сечение параллелепипеда плоскостью, проходящей через указанные точки (рисунок 4). Рисунок 4 Учитель выполняет построение на доске, учащиеся в своих тетрадях. Можно вызвать к доске одного из учеников. 4. Решение задачи №79 (а). Один ученик выполняет чертёж на доске. Учитель. Изобразите параллелепипед ABCDA' B'C'D' и постройте его сечение плоскостью АВС'. Докажите, что полученное сечение является параллелограммом. При объяснении построения и при доказательстве учащиеся должны учитывать свойство граней параллелепипеда и правила для построения сечений. Построение сечений в тетраэдре по чертежам, заранее начерченных на доске (желательно с обратной стороны). Задание1. Построить сечение плоскостью, проходящей через точку М, параллельно основанию АВС. (Подсказка: воспользуйтесь признаком параллельности прямой и плоскости и признаком параллельности двух плоскостей). Задание2. Построить сечение тетраэдра плоскостью, проходящей через точки М, N и P, если NP BC. (Подсказка: вспомните свойства параллельных плоскостей). Задание3. Построить сечение плоскостью MNP. (Подсказка: вспомните решение домашних задач и примените их для построения). Рисунок 4 Ученики выполняют построения в тетрадях, учитель проверяет, при необходимости исправляет, помогает при затруднениях, оценивает учеников, выполнивших два или три задания. При выполнении задания большинством учеников, чертежи выполняются и на доске одним из учеников. 5. Объяснение наиболее сложной задачи на построение сечения параллелепипеда плоскостью, проходящей через три данные точки. (слайд 3). Примерные вопросы для фронтальной беседы с классом при показе слайда: Как построить прямую, по которой секущая плоскость пересекает плоскость нижнего основания? По каким прямым секущая плоскость пересекает верхнее и нижнее основания параллелепипеда? Через какую точку проходит прямая, параллельная прямой АЕ? 6. После показа построения ученики выполняют построение в тетрадях. (При необходимости слайд можно показать повторно). 7. Итог урока. Давайте вспомним этапы построения сечений тетраэдра (параллелепипеда, куба). Какие многоугольники могут при этом получиться? 8. Задание на дом: §4, п.14, решить задачи №79(б), 82, для более сильных учеников №114.