Домашнее задание по факультативу «Теория вероятностей и

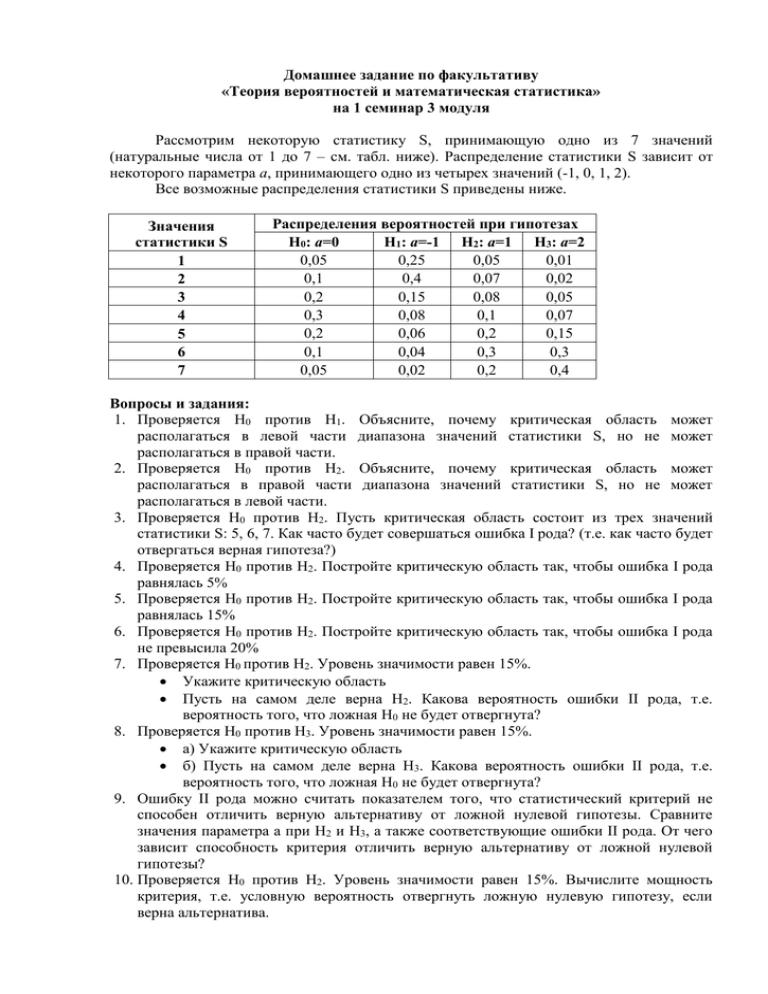
Домашнее задание по факультативу
«Теория вероятностей и математическая статистика»
на 1 семинар 3 модуля
Рассмотрим некоторую статистику S, принимающую одно из 7 значений
(натуральные числа от 1 до 7 – см. табл. ниже). Распределение статистики S зависит от
некоторого параметра a, принимающего одно из четырех значений (-1, 0, 1, 2).
Все возможные распределения статистики S приведены ниже.
Значения
статистики S
1
2
3
4
5
6
7
Распределения вероятностей при гипотезах
H0: a=0
H1: a=-1 H2: a=1 H3: a=2
0,05
0,25
0,05
0,01
0,1
0,4
0,07
0,02
0,2
0,15
0,08
0,05
0,3
0,08
0,1
0,07
0,2
0,06
0,2
0,15
0,1
0,04
0,3
0,3
0,05
0,02
0,2
0,4
Вопросы и задания:
1. Проверяется H0 против H1. Объясните, почему критическая область может
располагаться в левой части диапазона значений статистики S, но не может
располагаться в правой части.
2. Проверяется H0 против H2. Объясните, почему критическая область может
располагаться в правой части диапазона значений статистики S, но не может
располагаться в левой части.
3. Проверяется H0 против H2. Пусть критическая область состоит из трех значений
статистики S: 5, 6, 7. Как часто будет совершаться ошибка I рода? (т.е. как часто будет
отвергаться верная гипотеза?)
4. Проверяется H0 против H2. Постройте критическую область так, чтобы ошибка I рода
равнялась 5%
5. Проверяется H0 против H2. Постройте критическую область так, чтобы ошибка I рода
равнялась 15%
6. Проверяется H0 против H2. Постройте критическую область так, чтобы ошибка I рода
не превысила 20%
7. Проверяется H0 против H2. Уровень значимости равен 15%.
 Укажите критическую область
 Пусть на самом деле верна H2. Какова вероятность ошибки II рода, т.е.
вероятность того, что ложная H0 не будет отвергнута?
8. Проверяется H0 против H3. Уровень значимости равен 15%.
 а) Укажите критическую область
 б) Пусть на самом деле верна H3. Какова вероятность ошибки II рода, т.е.
вероятность того, что ложная H0 не будет отвергнута?
9. Ошибку II рода можно считать показателем того, что статистический критерий не
способен отличить верную альтернативу от ложной нулевой гипотезы. Сравните
значения параметра a при H2 и H3, а также соответствующие ошибки II рода. От чего
зависит способность критерия отличить верную альтернативу от ложной нулевой
гипотезы?
10. Проверяется H0 против H2. Уровень значимости равен 15%. Вычислите мощность
критерия, т.е. условную вероятность отвергнуть ложную нулевую гипотезу, если
верна альтернатива.
11. Проверяется H0 против H3. Уровень значимости равен 15%. Вычислите мощность
критерия
12. Сформулируйте выводы, сделанные Вами в п.9, на язык мощности критерия.
13. Проверяется H0 против H2. Вычислите вероятность ошибки II рода, если уровень
значимости равен 15%; если уровень значимости равен 5%.
14. На основе п.13 сделайте вывод о связи уровня значимости и вероятности ошибки II
рода; уровня значимости и мощности критерия
15. Объясните, почему НЕверно, что вероятность ошибки II рода равна 1 - вероятность
ошибки I рода
16. Проверяется H0 против сложной гипотезы a ≠ 0. Постройте критическую область так,
чтобы уровень значимости не превысил 30%.
17. Проверяется H0 против сложной гипотезы a ≠ 0. Уровень значимости равен 30%.
Вычислите мощность критерия.
18. Объясните, почему на практике проще установить фиксированный уровень
значимости, чем фиксированную вероятность ошибки II рода.
19. Увеличение доверительной области (т.е. уменьшение критической области) повышает
вероятность ошибки второго рода. Тем не менее, иногда оказывается возможным
уменьшить критическую область, не повышая вероятность ошибки второго рода.
Объясните, почему статистики стремятся к этому.
20. Если нулевая гипотеза отвергнута, это может означать одно из двух:
a. либо имеющиеся данные и условия проверки гипотезы позволили критерию
отличить верную альтернативу от ошибочной нулевой гипотезы,
b. либо произошло редкое при нулевой гипотезе событие, и мы допустили
ошибку первого рода
Продолжая эту логику, объясните, почему в обратной ситуации правильно говорить,
что «нулевая гипотеза не отвергнута», а не «нулевая гипотеза принята».