Тема 5. Геометрический и механический смысл производной. Неравенства с одной переменной
реклама
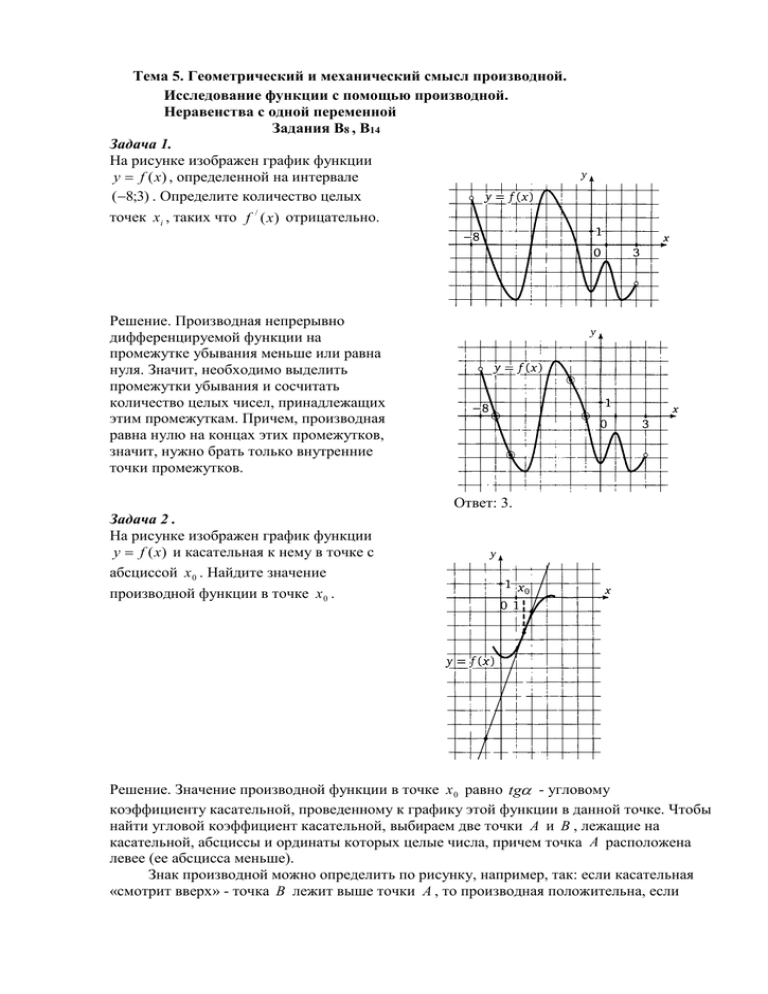
Тема 5. Геометрический и механический смысл производной. Исследование функции с помощью производной. Неравенства с одной переменной Задания В8 , В14 Задача 1. На рисунке изображен график функции y f (x) , определенной на интервале (8;3) . Определите количество целых точек xi , таких что f / ( x) отрицательно. Решение. Производная непрерывно дифференцируемой функции на промежутке убывания меньше или равна нуля. Значит, необходимо выделить промежутки убывания и сосчитать количество целых чисел, принадлежащих этим промежуткам. Причем, производная равна нулю на концах этих промежутков, значит, нужно брать только внутренние точки промежутков. Ответ: 3. Задача 2 . На рисунке изображен график функции y f (x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции в точке x 0 . Решение. Значение производной функции в точке x 0 равно tg - угловому коэффициенту касательной, проведенному к графику этой функции в данной точке. Чтобы найти угловой коэффициент касательной, выбираем две точки A и B , лежащие на касательной, абсциссы и ординаты которых целые числа, причем точка A расположена левее (ее абсцисса меньше). Знак производной можно определить по рисунку, например, так: если касательная «смотрит вверх» - точка B лежит выше точки A , то производная положительна, если точка B ниже, то отрицательна, если касательная горизонтальна, то производная равна нулю. Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC (см. рисунок). BC Модуль углового коэффициента будет равен . Найдем координаты точек: A(1;10) , CA 9 B ( 2;1) , C (2;10) , тогда BC 9, AC 3 . tg = 3 . 3 Ответ: 3. При решении этой задачи важно помнить, что тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету. Также можно использовать следующее рассуждение: так как уравнение касательной имеет вид y kx b и f ( x) k , найдя координаты точек A( x0 ; y 0 ) и B( x1 ; y1 ) , лежащих на касательной, мы можем найти k из системы уравнений y0 k * x0 b, y1 k * x1 b. 10 1k b, В нашей задаче k 3. 1 2k b. Задача 3. Найдите точку минимума функции y (0,5 x) cos x sin x , принадлежащую промежутку (0; ) . 2 Решение. Найдем производную данной функции, применив правило для вычисления производной произведения двух функций: y (0,5 x) cos x (0,5 x)(cos x) cos x cos x (0,5 x) sin x cos x ( x 0,5) sin x . На промежутке (0; ) производная обращается в нуль только при x 0,5 , поскольку 2 sin x 0 на этом промежутке. В точке x 0,5 производная меняет знак с минуса на плюс, и эта точка является единственной точкой минимума. Ответ: 0,5. Задания для самостоятельной работы Задания В8 1) На рисунке изображен график функции y f (x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции в точке x 0 . 2) На рисунке изображен график функции y f (x) . Касательная к этому графику, проведенная в точке x 4 , проходит через начало координат. Найдите f (4). 3) На рисунке изображен график функции y f (x) , определенной на интервале (1;13) . Определите количество целых чисел xi , таких, что f ( xi ) отрицательно. 4) На рисунке изображен график движения точки по прямой. По горизонтали отложено время, по вертикали – расстояние от точки отсчета. Сколько раз за наблюдаемый период точка останавливалась? 5) Прямая y 5 x 6 параллельна касательной к графику функции y x 2 8 x 3 . Найдите абсциссу точки касания. 6) На рисунке изображен график производной функции y f (x) , определенной на интервале (10;3) . В какой точке отрезка 4;1 f (x ) принимает наибольшее значение? 7) На рисунке изображен график производной функции, определенной на интервале (3;8) . Найдите промежутки убывания функции y f (x) . В ответе укажите сумму целых чисел, входящих в эти промежутки. Задания В14 1) Найдите точку максимума функции y 9 4 x 4 x 2 x 3 . 2) Найдите наименьшее значение функции y (1 x)( x 4) 2 на отрезке 0;3 . 3) Найдите точку максимума функции y 2 cos x (5 2 x) sin x 4, принадлежащую промежутку ; . 2 4) Найдите наименьшее значение функции y 5 ( x 3)e 4 x на отрезке 0;7. 5) Найдите точку минимума функции y 2 x 5 ln( x 7) . 6) Найдите наибольшее значение функции x3 x2 9 y x 2 на отрезке 9;1 . x Задания С3 Решите системы неравенств (2 x 32)(3 x 27) 0, 1) x 2 5 x 14 log 0,1 2 x 1 0. 3 x 1 12 * 3 x , 2) log ( x 2 4 x 3) 2 log (4 x) 0. 1 13 3 (9 x 4) 0, log 3) x logx 2 x x x 6 4 * 3 2 4 0. 4) Решите неравенство log 3 x ( x 2 10 x 25) 2 log 3 x (4 x x 2 5) 2.