В 8 классе (геометрия) после прохождения темы «Четырёхугольники» я

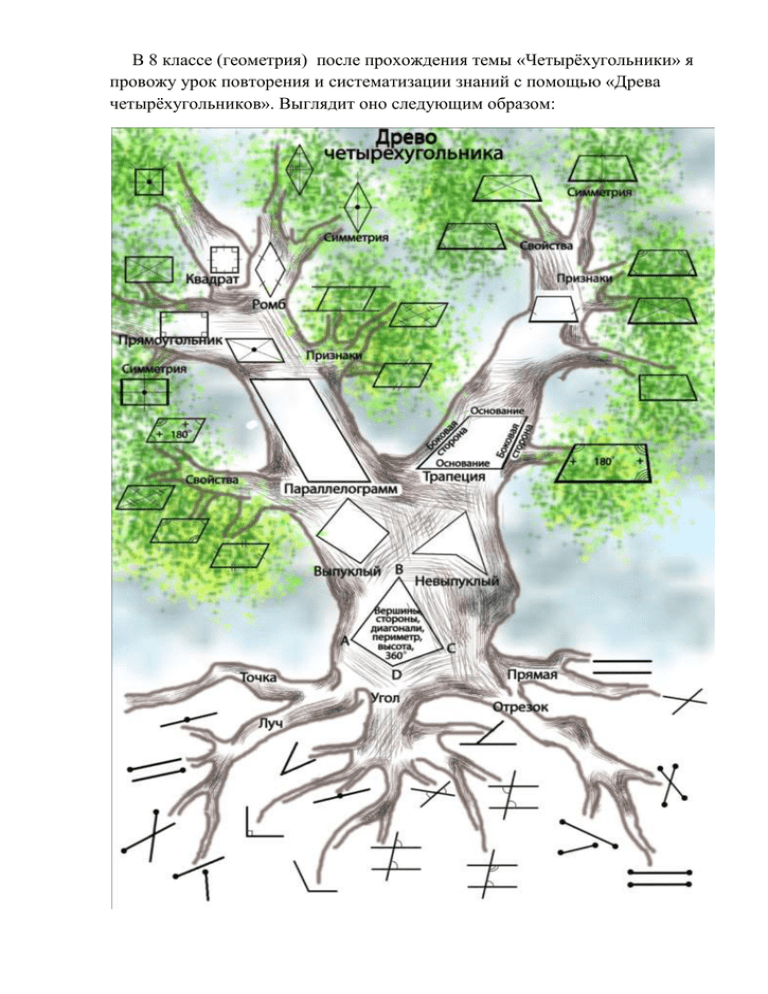
В 8 классе (геометрия) после прохождения темы «Четырёхугольники» я
провожу урок повторения и систематизации знаний с помощью «Древа
четырёхугольников». Выглядит оно следующим образом:
Этот вариант «Древа» разработан мною. Каждый ученик по моему
шаблону создаёт своё «Древо» и по нему ведёт рассказ о четырёхугольниках.
Рассказ занимает около 5 минут.
Данное «Древо» является планом, с помощью которого учащиеся
рассказывают теоретические сведения, связанные с данной темой, включая
тему «Симметрия».
Рассказ начинается с корней дерева (снизу) и постепенно поднимается
наверх. Выглядеть этот рассказ может следующим образом:
«Основные фигуры в геометрии это точка и прямая. Из этих фигур
получаются следующие: отрезок, луч и угол. Все эти фигуры используются в
четырёхугольнике.
Четырёхугольником называется геометрическая фигура, состоящая из трёх
точек, причём никакие три не лежат на одной прямой, и отрезков,
соединяющие эти точки, причём никакие отрезки не пересекаются, кроме
соседних. Эти точки называются вершинами, отрезки – сторонами. Вершины
называются соседними, если они являются концами одной стороны.
Периметром называется сумма длин его сторон. Диагональю называется
отрезок, соединяющий не соседние вершины. Высотой называется
перпендикуляр, проведённый из вершины четырёхугольника к противолежащей
стороне. Сумма углов в четырёхугольнике равна 360°.
Четырёхугольники бывают выпуклые и невыпуклые. Выпуклым называется
четырёхугольник, вершины которого расположены по одну сторону от прямой,
проходящей через каждую его сторону.
Существует два вида четырёхугольников: параллелограмм и трапеция.
Параллелограммом
называется
четырёхугольник,
у
которого
противолежащие стороны попарно параллельны. В параллелограмме
выполняются следующие свойства: противолежащие стороны равны;
противолежащие углы равны; диагонали точкой пересечения делятся пополам;
сумма углов прилегающих к каждой стороне равна 180°.
Существует три признака параллелограмма: если в четырёхугольнике две
стороны равны и параллельны, то это параллелограмм; если в
четырёхугольнике противолежащие стороны равны, то это параллелограмм;
если в четырёхугольнике диагонали точкой пересечения делятся пополам, то
это параллелограмм.
У параллелограмма есть центр симметрии – это точка пересечения его
диагоналей.
Существует три вида параллелограммов: прямоугольник, ромб и квадрат.
Прямоугольником называется параллелограмм, у которого все углы прямые.
У прямоугольника есть свойство: диагонали его равны. Есть признак: если в
параллелограмме диагонали равны, то это прямоугольник. У прямоугольника
есть центр симметрии – точка пересечения диагоналей и две оси симметрии –
прямые проходящие через середины противолежащих сторон.
Ромбом называется параллелограмм, у которого все стороны равны.
Свойство ромба: в ромбе диагонали взаимно перпендикулярны и являются
биссектрисами своих углов. В ромбе есть центр симметрии – точка
пересечения диагоналей и две оси симметрии – прямые, проходящие по его
диагоналям.
Квадратом называется: а) параллелограмм, у которого все углы прямые и
все стороны равны; б) прямоугольник, у которого все стороны равны; в) ромб,
у которого все углы прямые. У квадрата выполняются все свойства
предыдущих фигур. У квадрата есть центр симметрии и 4 оси симметрии:
прямые, проходящие через середины противолежащих сторон и по его
диагоналям.
Трапецией называется четырёхугольник, у которого две стороны
параллельны, а две другие нет. Параллельные стороны называются
основаниями, а две другие – боковыми. У трапеции сумма углов, прилегающих к
боковым сторонам равна 180°.
Трапеции бывают равнобедренные и прямоугольные.
Равнобедренной трапецией называется трапеция, у которой боковые
стороны равны. У равнобедренной трапеции углы при основаниях равны и
диагонали равны – это свойства. Есть признаки: если у трапеции углы при
основании равны, то она равнобедренная; если у трапеции диагонали равны, то
она равнобедренная. У равнобедренной трапеции есть ось симметрии – прямая,
проходящая через середины оснований.
Прямоугольной трапецией называется трапеция, у которой боковая сторона
перпендикулярна основаниям.»
Задача слушающих учеников – отметить неточности или отсутствующие
сведения и факты. Вести учёт ответа удобно с помощью следующего листа:
Древо четырёхугольника _____________
содержание
наличие
Устный
ответ
/40
/40
Четырёхугольник
Определение четырёхугольника
Определение вершин, сторон
Определение диагонали
Определение периметра
Определение высоты
Сумма углов
Определение выпуклого четырёхугольника
Параллелограмм
Определение параллелограмма
Свойство противолежащих сторон
Свойство противолежащих углов
Свойство диагоналей
Свойство углов, прилегающих к каждой стороне
Признак параллелограмма через противолежащие стороны
Признак через две стороны
Признак через диагонали
Симметрия в параллелограмме
Прямоугольник
Определение прямоугольника
Свойство прямоугольника
Признак прямоугольника
Симметрия в прямоугольнике: а) осевая; б) центральная
Ромб
Определение ромба
Свойство ромба
Симметрия в ромбе: а)осевая; б) центральная
Квадрат
Определение квадрата через параллелограмм
Определение квадрата через прямоугольник
Определение квадрата через ромб
Симметрия в квадрате а) осевая; б) центральная
Трапеция
Определение трапеции
Названия сторон в трапеции
Свойство трапеции
Определение равнобедренной трапеции
Свойство р/б трапеции через углы
Свойство р/б трапеции через диагонали
Признак р/б трапеции через углы
Признак р/б трапеции через диагонали
Определение прямоугольной трапеции
Симметрия в трапеции
Итого
Оценка
Затем каждый ученик пишет рецензию на ответ. Возможно устное
коллективное обсуждение ответа ученика.
После этого проводится конкурс на лучшее «Древо четырёхугольников»
(выставка рисунков).
Оценивается каждое древо по нескольким номинациям: наполняемость
фактами; эстетичность; аккуратность; исполнение (компьютерное, с
применением фотографий, рисунок от руки).
К «Древу четырёхугольников» возвращаемся в следующей теме
«Площади». Древо дополняется подписями формул площадей. Затем это
древо используется в теме «Вписанная и описанная окружности» и при
повторении материала в 9 классе при подготовке к экзаменам.
Все работы хранятся у учителя для использования при изучении различного
материала.
Такая форма повторения теории очень эффективна: ребята с
удовольствием выполняют эту творческую работу, что способствует
лучшему усвоению теоретического материала.