Параллельность плоскостей
реклама
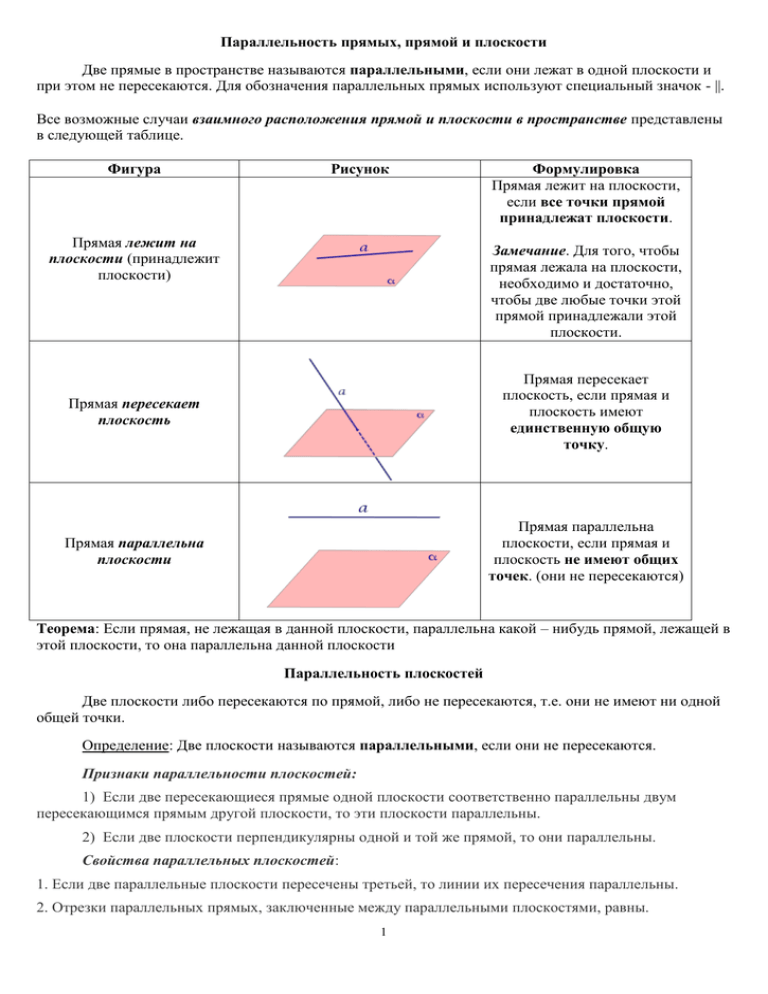
Параллельность прямых, прямой и плоскости Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и при этом не пересекаются. Для обозначения параллельных прямых используют специальный значок - ||. Все возможные случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице. Фигура Рисунок Прямая лежит на плоскости (принадлежит плоскости) Формулировка Прямая лежит на плоскости, если все точки прямой принадлежат плоскости. Замечание. Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости. Прямая пересекает плоскость Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку. Прямая параллельна плоскости Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются) Теорема: Если прямая, не лежащая в данной плоскости, параллельна какой – нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости Параллельность плоскостей Две плоскости либо пересекаются по прямой, либо не пересекаются, т.е. они не имеют ни одной общей точки. Определение: Две плоскости называются параллельными, если они не пересекаются. Признаки параллельности плоскостей: 1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. 2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны. Свойства параллельных плоскостей: 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. 1