Расчет рамы методом перемещений» / Сост.

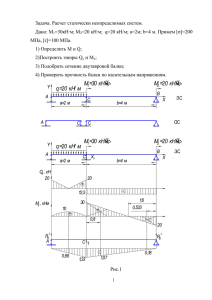
УДК 624.04 (075)
ББК 38112
Г96
Г96
Методические указания к выполнению расчетно-графической работы
«Расчет рамы методом перемещений» / Сост.: С.В.Гусев. – Казань: КГАСУ,
2012.-26с.
Печатается по решению Редакционно-издательского совета Казанского
государственного архитектурно-строительного университета
В методических указаниях изложены основные понятия и формулы
расчета статически неопределимой рамы методом перемещений. Рассмотрены
решения примеров. Приведены примеры тестовых задач.
Рецензент
Доктор физико-математических наук, профессор, заведующий кафедрой
сопротивления материалов и основ теории упругости
Р.А. Каюмов
УДК 624.04 (075)
ББК 38112
© Казанский государственный
архитектурно-строительный
университет, 2012
© Гусев С.В.,2012
2
ВВЕДЕНИЕ
В методе перемещений в качестве неизвестных принимаются
перемещения узлов заданной системы (ЗС).
Идея метода заключается в том, чтобы воспользоваться таблицей 1
готовых решений для построения эпюр моментов. Для этого надо добавить
фиктивные связи в узлы системы, чтобы они стали неподвижными. При этом
заданная система распадается на однопролетные балки, которые будут
воспринимать только те нагрузки, которые приложены непосредственно к ним.
Эпюры моментов от этих нагрузок сведены в таблицу 1 стандартных решений.
Система с неподвижными узлами называется кинематически определимой. На
рис. 5-7 стр. 14-23 приведены три примера, разделы которых соответствуют
порядку решения задач методом перемещений. Изучение разделов
целесообразно после ознакомления с контрольными вопросами по теме,
приведенными в конце методических указаний.
1. Определение степени кинематической неопределимости заданной
системы
Степень кинематической неопределимости определяется по формуле
n = nу + nл,
(1)
где nу – число угловых степеней свободы равно числу свободных жестких узлов
заданной системы, nл – число линейных степеней свободы узлов.
Для определения nл надо превратить заданную систему в ферму путем
введения полных шарниров во все узлы и опорные связи и определить степень
свободы ее узлов по формуле:
Wф=2∙У-С-Со,
где У - число узлов фермы, С - число стержней, Со - число опорных связей.
Если полученная ферма является механизмом (Wф > 0), то nл равно
минимальному числу опорных связей, которые необходимо добавить в узлы
фермы, чтобы они стали неподвижными.
Количественная часть кинематического анализа не является достаточным
условием для определения числа степеней свободы сооружения. Например, для
фермы (рис. 6,б) полученной из заданной системы, Wф = -1. Однако,
качественный анализ выявляет одну степень свободы Wф = 1, поскольку данная
ферма является мгновенно изменяемой конструкцией (МИК), так как три диска
(рис. 6,в): «диск Земля» (фундамент сооружения) и два диска (стержни 1-3 и 35) крепятся тремя шарнирами в точках 1, 3, 5, которые лежат на одной прямой.
Для превращения ее в кинематически определимую требуется ввести в узел 4
одну горизонтальную опорную связь.
3
2. Выбор основной системы (ОС)
Основная система получается из заданной путем введения
дополнительных связей в ее узлы, которые обеспечивают их неподвижность. В
свободные жесткие узлы добавляют фиктивные заделки, которые лишают их
угловой степени свободы. Опорные связи помещают по направлению степеней
свободы фермы, полученной из заданной системы. Они лишают все свободные
узлы линейных степеней свободы.
В основной системе два вида воздействий: известные активные силы и
неизвестные перемещения во вновь введенных связях. В фиктивной заделке
неизвестной является ее угол поворота, в опорной связи – ее линейное
смещение. Направления неизвестных перемещений, принятые в основной
системе, считаются положительными при расчетах и совпадают с
положительными направлениями реакций, которые в них возникают в грузовом
и единичных состояниях. Число неизвестных Zi равно сумме угловых и
линейных степеней свободы nу и nл, определяемых по формуле (1). Основная
система с минимальным количеством связей, необходимых для неподвижности
узлов, является единственной.
Рис.1
Для уменьшения числа неизвестных Zi используется два предположения.
Во-первых, стержни в жестком узле поворачиваются на один и тот же угол (φ12
= φ23 = Z1, рис. 1в), тогда любой свободный жесткий узел обладает только
одной угловой степенью свободы. Во-вторых, в стержнях не учитываются
деформации растяжения-сжатия и сближение концов стержней после
деформации (U2 = U 3 = Z2 , рис. 1в). Основная система (рис. 1в) получается
путем внедрения в заданную систему двух связей: фиктивной заделки в узел 2 и
горизонтальной опорной связи в узел 3.
Заданная система на рис. 5,а имеет один жесткий узел, следовательно,
nу= 1. Все узлы фермы (рис. 5,б), полученной из заданной системы,
4
неподвижны и nл = 0. Основная система получается путем внедрения в жесткий
узел 2 фиктивной заделки (рис. 5,в).
В заданной системе на рис. 6,а нет свободных жестких узлов,
следовательно, nу = 0. Соответствующая ферма (рис. 6,б) имеет одну степень
свободы, поэтому nл = 1. Основная система (рис. 6,г) получается введением в
узел 4 горизонтальной опорной связи.
В заданной системе на рис. 7,а один свободный жесткий узел,
следовательно, nу = 1. Ферма (рис. 7,б), полученная из заданной системы, имеет
одну степень свободы, поэтому nл = 1. Основная система (рис. 7,в) получается
путем внедрения в заданную систему двух связей: фиктивной заделки в узел 2 и
горизонтальной опорной связи в узел 3.
3. Составление системы канонических уравнений
Число канонических уравнений равно числу введенных связей в заданной
системе, каждое из которых имеет смысл уравнения равновесия, отражающих
отсутствие реакции во вновь введенной связи в основной системе, так как в
заданной системе этой связи не существует.
На основании принципа суперпозиции, из основной системы выделяются
грузовое состояние (ГС) и единичные состояния (ЕС). В каждом состоянии от
соответствующих воздействий во вновь введенных связях возникают реакции,
которые являются коэффициентами канонических уравнений.
Если деформация заданной системы зависит от одного перемещения:
углового или линейного (рис. 5 , 6), то каноническое уравнение имеет вид
R1 = r11 Z1 + R1p = 0.
(2)
Это условие эквивалентности заданной и основной систем называется
каноническим уравнением потому, что его вид одинаков для любой один раз
кинематически неопределимой системы.
Для задачи на рис. 5 - Z1 - угол поворота фиктивной заделки, r11 - момент
фиктивной заделки в единичном состоянии, где воздействием является
единичный угол поворота; R1p - момент фиктивной заделки в грузовом
состоянии от внешней нагрузки. Если единичный угол поворота увеличить в Z1
раз, то момент заделки r11 увеличивается тоже в Z1 раз. Необходимо подобрать
величину угла поворота Z1 так, чтобы суммарная реакция от нагрузки R1p и r11
Z1 в основном состоянии была равна нулю (R1=0), так как в действительности в
заданной системе фиктивной заделки не существует.
Для задачи на рис. 6 - Z1 – неизвестное линейное перемещение введенной
горизонтальной опоры, r11 – ее реакция в единичном состоянии, где
воздействием является единичное горизонтальное смещение опоры; R1p –
реакция во введенной опоре от внешней нагрузки.
5
Если деформированное состояние заданной системы описывается двумя
неизвестными перемещениями (для задачи на рис. 7), то составляется два
уравнения равновесия.
R1 = r11 Z1 + r12 Z2 + R1p = 0,
(3)
R2 = r21 Z1 + r22 Z2 + R2p = 0.
Для трех неизвестных канонические уравнения имеют вид (рис. 2)
В общем случае rij – реакции в i – ой связи в j – ом – единичном
состоянии; Rip - реакции в i – ой связи в грузовом состоянии.
Рис. 2
В единичных
состояниях воздействиями являются единичные
перемещения введенных связей. В первом и втором единичных состояниях –
это поворот фиктивной заделки на единичный угол, в третьем – единичное
смещение горизонтальной опоры
6
4. Определение коэффициентов канонических уравнений
Для определения коэффициентов строятся эпюры в грузовом и
единичном состояниях. При построении используются готовые решения из
таблицы 1, которые переносятся так, чтобы эпюра моментов оказалась со
стороны растянутых волокон. Для выявления растянутых волокон оси балок в
деформированном состоянии изображаются пунктиром.
Коэффициенты являются реакциями во вновь введенных связях. Их
положительные значения указываются в основной системе. Неизвестный
момент фиктивной заделки определяется из уравнения равновесия узла,
содержащего ее. Коэффициенты, являющиеся усилиями во введенных опорных
связях, определяются из уравнения проекций всех сил на ось, параллельную
этой связи для всей конструкции или для кругового сечения, которое
пересекает эту связь.
5. Проверка коэффициентов канонических уравнений
Каждый коэффициент можно проверить кинематическим способом по
формулам:
где Mp0- эпюра моментов от нагрузки в статически определимой системе,
полученной из заданной системы путем удаления всех лишних связей. Знак «×»
обозначает интеграл Мора [1], который вычисляется по формуле Симпсона (5)
или Верещагина (6). Найденный коэффициент сравнивается со значением,
полученным статическим способом.
где m – количество участков на эпюре, L – длина участка, “л”,“с”,“п” –
соответственно левое, среднее, правое значения на участке эпюры. Знак
произведения положительный, если оба значения лежат по одну сторону от оси
балки. Ω - площадь первой эпюры, Ус – ордината на второй эпюре, взятая под
центром тяжести первой эпюры. Если одна эпюра криволинейная, то берется ее
площадь.
Например, в задаче 5 коэффициент r11 можно получить перемножением
единичной эпюры (рис. 3,а) на себя , а коэффициент R1p - перемножением
эпюры Mp0 на M 1. На рис. 3,б,в приведена статически определимая система под
действием заданных нагрузок и ее эпюра моментов Mp0.
7
Рис.3
Для задач один раз кинематически неопределимых в канонических
уравнениях коэффициентов всего два, и целесообразность их проверки
невелика, поэтому раздел 5 в примерах на рис. 5 и 6 отсутствует.
Для n ≥ 2 перед решением канонических уравнений целесообразно
проверить правильность вычислений коэффициентов. На основании теоремы
Релея о взаимности реакций [1] в канонических уравнениях коэффициенты,
симметрично расположенные относительно главной диагонали, должны быть
равны, то есть rij = r ji . Например, при n = 2 по теореме Релея равны между
собой два коэффициента (7). Не целесообразно проверять каждый коэффициент
по отдельности, поскольку должна выполняться универсальная проверка
коэффициентов rij (8) и проверка грузовых коэффициентов (9)
где Ms - суммарная эпюра получается путем сложения ординат единичных
эпюр. Проверки (8), (9) выполнены в примере на рис. 7.
8
6. Решение системы канонических уравнений
Для систем один раз кинематически неопределимых (n=1) каноническое
уравнение (2) одно и решение имеет вид
Для систем два раза кинематически неопределимых решение
системы уравнений (3) и (4) имеет вид:
7. Построение окончательной эпюры изгибающих моментов Мок.
Окончательная эпюра Мок в соответствии с принципом независимости
действия сил получается путем сложения «исправленных» эпюр M ∙Zi с
грузовой:
«Исправленные» эпюры M ∙Zi получаются путем увеличения всех
ординат единичных эпюр в Zi раз. Если Zi < 0, то измененные ординаты
откладываются с другой стороны от оси стержня.
Каждое значение на эпюре Мок получается по формуле (10). Например,
на рис. 7,п значение момента в узле 4 равно сумме момента М4,р в узле 4
грузового состояния рис 7,ж и моментов М4,1, М4,2 в узле 4 в первом и втором
единичных состояниях рис. 7.н и 7.о. Значения слева от оси балки приняты
положительными
М4,ок = М4,р + М4,1 + М4,2 = 2 + 5.417 – 0.9445 = 6.4725 кН∙м.
8. Проверка правильности построения эпюры Мок
Перед построением эпюр Q и N целесообразно убедиться в
правильности эпюры Мок, то есть провести статическую проверку. Поскольку
Мок строится в основной системе, то в ней проверяется отсутствие реакций во
вновь введенных связях. Эта проверка равновесия узла является необходимым
условием правильности значений моментов, примыкающих к фиктивным
заделкам и круговым сечениям, содержащим вновь введенные связи.
Для проверки остальных значений необходимо превратить заданную
систему в статически определимую путем отбрасывания лишних связей. В
9
полученной системе вычислить перемещения по направлению какой-либо
отброшенной лишней связи. Если перемещение отсутствует, то значения
моментов в эпюре Мок, участвующие в вычислении, верны.
Максимальное значение момента в Мок (рис. 5) не примыкает к
фиктивной заделке и не участвует в статической проверке (R1=0). Ммах будет
участвовать в определении перемещения  3гор .
Статическая проверка эпюры Мок не дает проверить максимальный
момент в точке 2 (рис. 6). Для его проверки надо получить статически
определимую систему. В разделе 1 кинематический анализ установил, что
заданная система пять раз статически неопределима. В узлах 1 и 6 убрано по
две связи: линейная по вертикали и угловая, а в узле 5 – угловая связь (рис. 6,к).
Значение Ммах входит в проверку отсутствия угла поворота в узле 5.
Отсутствие реакции во вновь введенной опорной связи R1 и момента
фиктивной заделки R2 показано на рис. 7,р и 7,с. Для достоверности Ммах
проверяется отсутствие вертикального перемещения в узле 3 с помощью
интеграла Мора, причем единичная эпюра строится в статически определимой
системе (рис. 7,т).
9. Построение эпюр Q N
После определения неизвестных Zi основная система остается статически
неопределимой, поэтому уравнениями статики и методом сечения невозможно
воспользоваться для отыскания опорных реакций и построения эпюр.
Единственным способом построения эпюры Q является ее восстановление из

эпюры Мок по дифференциальной зависимости Журавского [1] Q 
. Для
x
участков, где эпюра Мок представляет собой наклонную прямую, поперечная
сила вычисляется по формуле
Q - положительна, если касательная в эпюре М совмещается с осью балки
против часовой стрелки.
По эпюре Мок рис. 7.п определяется модуль и знак поперечной силы Q
для балки 1-2 и нижнего участка балки 2-4.
10
В балке 2-3 Мок - парабола (рис. 7,п). Из параболы выделяются квадратичная
(рис. 4,б) и линейная (рис. 4,в) части. По этим эпюрам восстанавливаются
эпюры Q (рис. 4, д, е), которые затем складываются, что соответствует формуле
где QБАЛ – решение на рис. 7,д называется балочным.
Рис. 4
Значения эпюры N получаются по эпюре Q из уравнений равновесия
узлов. На рис. 7,у с эпюры Q стержней, образующих узел 2, снимаются
значения поперечных сил и наносятся на вырезанный узел так, что
положительные значения вращают узел по часовой стрелке (рис. 7,ф). Значения
продольных сил находятся из уравнений статики и наносятся на эпюру N (рис.
7,х).
Если узлов несколько, то последовательность их вырезания такова, чтобы
в уравнениях содержалось не более двух неизвестных.
10. Статическая проверка
Статическая проверка является достаточным условием правильности
решения задачи. По эпюрам М, Q, N в опорных связях восстанавливаются
значения реакций. Их направления определяются по правилу знаков:
положительные значения продольных сил N откладываются от сечения,
положительные значения поперечных сил Q вращают конструкцию по часовой
стрелке, моменты в заделках растягивают в стержнях ту сторону, с которой
построены эпюры. Уравнения равновесия должны выполняться.
11
Контрольные вопросы
Какая система называется кинематически определимой?
В чем состоит смысл метода перемещений?
Как определить степень кинематической неопределимости системы?
Как выбрать основную систему метода перемещений?
Как образовать «грузовое» и «единичные» состояния?
Каков физический смысл каждого канонического уравнения метода
перемещений?
7. Каков физический смысл неизвестных и коэффициентов канонических
уравнений метода перемещений?
8. Как определяются коэффициенты канонических уравнений в методе
перемещений?
9. Как проверить правильность построения окончательной эпюры моментов
в методе перемещений?
10.Как проверить правильность значений окончательной эпюры моментов,
не прилегающих к узлам?
11.Каков алгоритм расчета по методу перемещений?
1.
2.
3.
4.
5.
6.
Литература
1. Дарков А.В. Шапошников Н.Н. Строительная механика: Учебник. 9-ое
изд. испр. - СПб: Лань, 2004.-656с.
2. Шакирзянов Р.А. Краткий курс лекций по строительной механике.
Казань: КГАСУ, 2010. – 115с.
12
13
14
15
16
17
18
19
20
21
22
23
24
25
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению расчетно-графической работы
«Расчет рамы методом перемещений»
Составитель: Гусев Сергей Вячеславович
Редактор: Г.А. Рябенкова
Редакционно-издательский отдел
Казанского государственного архитектурно-строительного университета
Подписано к печати 15.05.12
Формат 60х84/16
Тираж 100 экз.
Печать ризографическая
Усл.-печ.л 1,63
Заказ № 284
Бумага офсетная № 1
Уч..-изд.л. 1,63
Печатно-множительный отдел КГАСУ
420043, Казань, Зеленая, 1
26