егэмат.2010

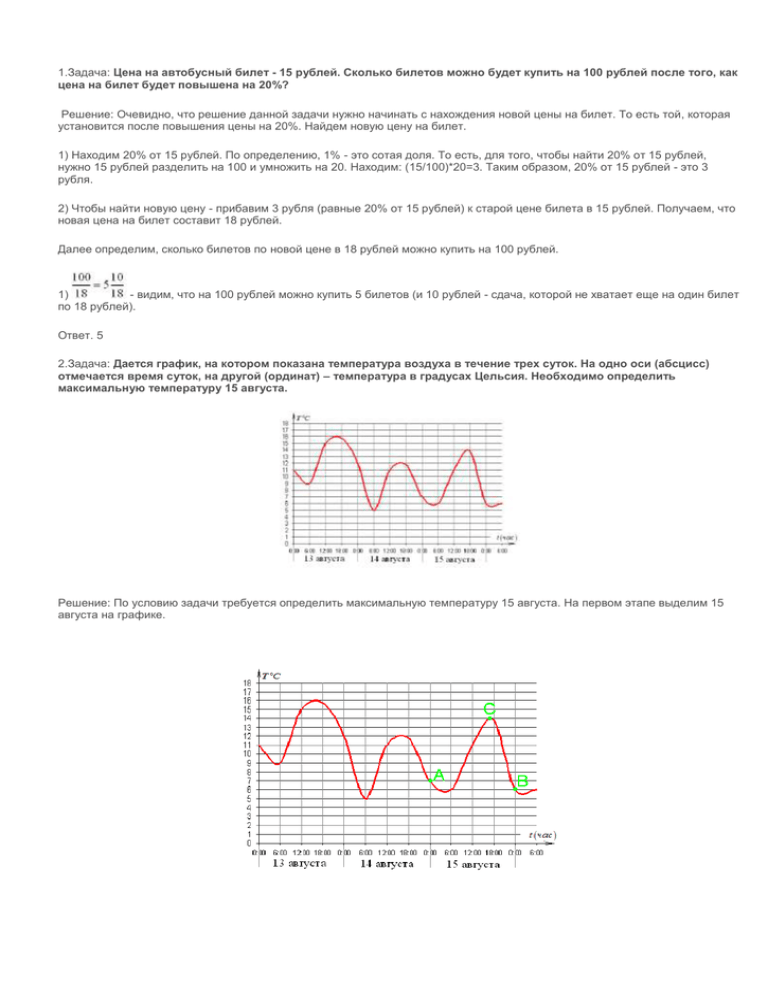
1.Задача: Цена на автобусный билет - 15 рублей. Сколько билетов можно будет купить на 100 рублей после того, как
цена на билет будет повышена на 20%?
Решение: Очевидно, что решение данной задачи нужно начинать с нахождения новой цены на билет. То есть той, которая
установится после повышения цены на 20%. Найдем новую цену на билет.
1) Находим 20% от 15 рублей. По определению, 1% - это сотая доля. То есть, для того, чтобы найти 20% от 15 рублей,
нужно 15 рублей разделить на 100 и умножить на 20. Находим: (15/100)*20=3. Таким образом, 20% от 15 рублей - это 3
рубля.
2) Чтобы найти новую цену - прибавим 3 рубля (равные 20% от 15 рублей) к старой цене билета в 15 рублей. Получаем, что
новая цена на билет составит 18 рублей.
Далее определим, сколько билетов по новой цене в 18 рублей можно купить на 100 рублей.
1)
- видим, что на 100 рублей можно купить 5 билетов (и 10 рублей - сдача, которой не хватает еще на один билет
по 18 рублей).
Ответ. 5
2.Задача: Дается график, на котором показана температура воздуха в течение трех суток. На одно оси (абсцисс)
отмечается время суток, на другой (ординат) – температура в градусах Цельсия. Необходимо определить
максимальную температуру 15 августа.
Решение: По условию задачи требуется определить максимальную температуру 15 августа. На первом этапе выделим 15
августа на графике.
На графике 15 августа мы отметили как AB. Очевидно, что наибольшей температуре в течение суток соответствует
наибольшее значение на промежутке AB. Это значение мы отметили буквой C. Наибольшая температура за 15 августа 14
градусов Цельсия.
3.Задача: Найти корень уравнения
.
Решение: Схема решения этого и подобных ему уравнений проста.
1) Привести левую и правую части уравнения к одному основанию.
2) Решить уравнение, приравняв показатели левой и правой частей уравнения.
В данном случае замечаем, что
. Сделаем в исходном уравнении замену:
Тогда по пункту 2) x-2=3. Отсюда получаем, что x=5.
Ответ. 5
4.Задание B4 – требует от ученика знания определений синуса, косинуса, тангенса и котангенса.
Задача: В треугольнике ABC дан угол С, равный 90 градусам, сторона AB равна 5, а косинус угла A равен 0,8.
Требуется найти длину стороны BC.
Решение: по определению косинус - это отношение прилежащего катета к гипотенузе. То есть, cos A = AC/AB. А значит,
0,8=AC/5. Отсюда имеем: AC=4. По теореме Пифагора находим BC:
образом, ВС=3
.Таким
5.Задание B5 требует от учеников внимательности. Никаких особенно глубоких знаний при решении данного задания не
понадобится.
Задача: Строительная компания должна купить 70 м3 пеноблоков. Имеется три поставщика. Условия доставки и
цены даны в таблице. Какая сумма потребуется для самой дешевой покупки с доставкой?
Поставщик Стоимость пеноблоков (руб.
за 1 м3)
1
2600
2
2800
3
2700
Стоимость доставки
(руб.)
10000
8000
8000
Дополнительные условия доставки
При заказе товара на сумму свыше 150000 рублей
доставка бесплатная
При заказе товара на сумму свыше 200000 рублей
доставка бесплатная
Решение: Определим, какую сумму потребуется заплатить каждому из поставщиков.
1 поставщик: 70*2600=182000, то есть, за 70 м 3 пеноблоков потребуется заплатить 182000 руб. К этой сумме добавляется
стоимость доставки: 182000+10000=192000 рублей. Таким образом, первому поставщику нужно будет заплатить 192000
рублей.
2 поставщик: 70*2800=196000, то есть, за 70 м 3 пеноблоков потребуется заплатить 196000 руб. В дополнительном условии
сказано, что при покупке товара на сумму свыше 150000 рублей доставка бесплатна. Таким образом, второму поставщику
нужно будет заплатить 196000 рублей.
3 поставщик: 70*2700=189000, то есть, за 70 м3 пеноблоков потребуется заплатить 189000 руб. К этой сумме добавляется
стоимость доставки: 189000+8000=197000 рублей. Таким образом, третьему поставщику нужно будет заплатить 197000
рублей.
Видно, что дешевле всего - купить пеноблоки у первого поставщика и эта покупка обойдется в 192000 рублей.
6.Задание B6 требует от ученика знания элементарных формул геометрии. У большинства учеников оно не вызывает
особых затруднений и может быть решено несколькими способами. Мы приведем одно из них и кратко опишем другие.
Задача: Дан четырехугольник, изображенный на клетчатой бумаге. Размер клетки: 1 см х 1 см. Требуется найти
площадь четырехугольника.
Решение: Как и любую новую неизвестную задачу, эту мы сведем к известной. Очевидно, что на рисунке изображен не
просто четырехугольник, а трапеция. Площадь трапеции вычисляется по формуле:
где h - высота, a, b - верхнее и нижнее основания. На рисунке видно, что высота трапеции равна 4 см, верхнее основание 3
см, а нижнее 6 см. Тогда по указанной выше формуле находим:
Таким образом, площадь трапеции равна 18 см2.
7.Задача: Найти значение выражения:
Решение: сведение данной задачи к известной можно осуществить с помощью известного свойства логарифмов:
по этой формуле имеем:
Таким образом, значение выражения равно 3.
8.Задача: На рисунке дан график функции y=f(x), а также касательная к графику в точке с абсциссой, равной 3. Найти
значение производной данной функции в точке х=3.
Решение: Для решения данной задачи необходимо вспомнить тот факт, что производная функции в точке равна тангенсу
угла, образованному касательной и осью Ox. То есть, f'(xo)=tg a.
f'(xo)=tg ACD.
Рассмотрим треугольник ADC и найдем tg ACD. По определению, тангенс равен отношению противоле
9.Задача: Дано два цилиндра. Объем первого равен 12 м3. Радиус основания второго в два раза меньше, чем
первого, а высота в три раза больше. Требуется найти объем второго цилиндра.
Решение: Объем цилиндра вычисляется по формуле:
Отметим радиус основания первого цилиндра r а высоту h. Тогда радиус основания второго цилиндра равен r/2,
а высота 3h. Подставим в указанную выше формулу и получим:
Упростим полученное выражение:
10.Задача: Камень был подброшен вверх вертикально. Пока он не упал, высота, на которой находится камень,
описывается формулой: h(t)=-5t2+18t (при этом, h - высота в метрах, а t - время в секундах, которое прошло с
момента броска). Определить, сколько времени камень был на высоте более 9 метров.
Решение: Очевидно, что камень может не долететь до отметки 9 метров, перелететь (и тогда отметку 9 метров он пролетит
дважды - когда будет лететь вверх и когда вниз), либо один раз - если высота его полета составит ровно 9 метров. Составим
и решим уравнение:
Таким образом, отметку в 9 метров камень пролетает дважды: на 0,6 и 3 секундах. Отсюда следует, что на высоте более 9
метров камень находился 2,4 секунды ( 3-0,6=2,4 ).
11.Задача: Найти наибольшее значение функции
на отрезке
Решение: Найдем критические точки. А для этого найдем производную функции, указанной выше, приравняем ее к нулю и
найдем корни уравнения, принадлежащие указанному выше отрезку:
Единственное решение, которое попадает в указанный выше отрезок:
Таким образом, наибольшее функции равно
или
Найдем указанные выше значения функции и найдем наибольшее:
Видно, что наибольшее значение функции равно 1.
12.Задача: Работая вместе, двое рабочих выполнят работу за 12 дней. Первый рабочий за два дня выполняет такую
же часть работы, как второй за три дня. За какое количество дней эту работу выполнит первый рабочий?
Решение: Примем за x - ту часть работы, которую выполняет первый рабочий, а за y - часть работы, которую выполняет
второй рабочий за 1 день. В условии задачи выделим два условия:
1) Первый рабочий за два дня выполняет такую же часть работы, как второй за три дня.
2) Работая вместе, двое рабочих выполнят работу за 12 дней.
Из первого условия получим первое уравнение системы:
а из второго:
Выразим из первого уравнения y и подставим во второе:
Из полученного уравнения выразим x:
То есть, первый рабочий за один день выполняет одну двадцатую часть работы. Очевидно, что на выполнение всей работы
ему потребуется 20 дней.
С1. .Задача: Решить систему уравнений:
Решение:
1) Видим, что первое уравнение системы содержит всего одну неизвестную переменную. Подобные уравнения часто
решают в школьном курсе математике и у вас оно не должно вызвать затруднений. Сделаем следующую замену:
Тогда первое уравнение системы можно переписать в следующем виде:
Решив данное уравнение, получим, что:
или
Отсюда получаем:
или
Обратите внимание на первое уравнение. Оно не имеет смысла (при решении ЕГЭ по математике вы должны это
учитывать). Решим второе уравнение:
Отсюда,
или
2) Итак, мы нашли значения x. Теперь подставим их во второе уравнение системы и найдем y.
а) Если
, то
чего, очевидно, не может быть, так как
б) Если
Ответ.
, то
,
С2. Задача: Дана правильная треугольная призма ABCA1B1C1, сторона основания которой равна 2, диагональ
боковой грани
. Найти угол между плоскостью A1BC и плоскостью основания призмы.
Решение: Обозначим середину ребра BC буквой H. Отрезки AH и A1H перпендикулярны BC, так как треугольник ABC равносторонний, а A1BC - равнобедренный. Следовательно, угол A1HA - линейный угол двугранного угла с гранями BCA и
BCA1.
Рассмотрим треугольник A1AB: по теореме Пифагора найдем AA1=1.
Рассмотрим треугольник AHB: по теореме Пифагора найдем AH=
Из треугольника HAA1 находим:
.
Отсюда находим: угол A1HA=30o.
С3. Задача: Решить неравенство:
Решение: Преобразуем неравенство:
Найдем, при каких значениях х левая часть имеет смысл:
Получаем:
Значит,
Сделаем замену
или
при всех допустимых значениях x. Поэтому,
. Получаем:
Таким образом,
откуда
Решив полученное квадратное уравнение, найдем корни: -6 и -1. Условию
только x=-1.
или
удовлетворяет
Ответ. -1.
С4. Задача: Дан угол ABC, равный 30о. На его стороне BA взята точка D такая, что AD=2 и BD=1. Найти радиус
окружности, касающейся прямой BC и проходящей через точки A, D
Решение: Центр О искомой окружности принадлежит серединному перпендикуляру к отрезку AD. Обозначим буквой P
середину AD, буквой Q - основание перпендикуляра, опущенного на прямую BC из точки O, буквой E - точку пересечения
прямой BC и серединного перпендикуляра. Отрезки OA, OD, OQ равны радиусу R окружности.
Заметим, что точка O не может лежать по ту же сторону от прямой AB, что и точка E, так как в этом случае расстояние от
точки O до прямой BC меньше, чем расстояние от нее до точки A.
Из прямоугольного треугольника BPE с катетом BP=2 и углом B=30o находим, что
Так как OA=R и AP=1, получим:
и, следовательно,
Из прямоугольного треугольника OQE, в котором угол E=60o, находим:
Таким образом, получаем следующее уравнение для R:
Данное уравнение легко приводится к квадратному возведением в квадрат левой и правой частей и приведением подобных
членов.
Решив данное уравнение, получим R1=1, R2=7.
Ответ. 1 или 7.
С5. Задача: Найти все значения параметра
, при которых уравнение
имеет хотя бы один корень.
Решение: Запишем уравнение в следующем виде:
.
Функция
непрерывна и
1) неограниченно возрастает при
, так как при любом раскрытии модулей будем иметь:
где
2) убывает при
где
, так как при любом раскрытии модулей будем иметь:
.
Следовательно, свое наименьшее значения функция
тогда, когда
.
примет при
, а уравнение
имеет корень тогда и только
Решим это неравенство:
С6. Задача: Найдите все такие пары взаимно простых натуральных чисел (то есть чисел, наибольший общий
делитель которых равен 1) и , что если к десятичной записи числа приписать справа через запятую десятичную
запись числа , то получится десятичная запись числа, равного
Решение: Пусть десятичная запись числа состоит из
цифр. Тогда по условию задачи можно записать равенство
, поэтому
Из этого уравнения следует, что
. Так как числа и взаимно простые, числа
(Действительно, пусть - общий простой делитель этих чисел. Тогда если делитель , то
- делитель , то будет делителем , значит, - делитель . Противоречие.)
Поэтому
случаях:
и, следовательно,
. Последнее равенство при взаимно простых
1)
, но в этом случае не выполняется равенство
2)
. В этом случае равенство
и
тоже взаимно простые.
будет делителем . Если же
и возможно только в двух
.
принимает вид
, откуда
Функция
возрастает, а функция
убывает. Поэтому уравнение
уравнения является
.
Ответ.
.
имеет не более одного корня, и так как
, единственным корнем