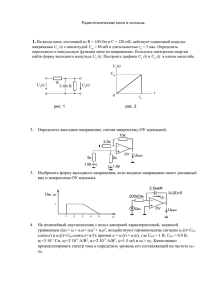
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Электрические цепи служат для передачи, изменения и преобразования проходящих через них сигналов. Элементы, из которых состоят
все электрические цепи, можно разделить на пассивные и активные.
Пассивными называют такие элементы электрической цепи, которые
не могут увеличивать энергию действующего в этой цепи сигнала. К
ним относятся сопротивление R, индуктивность L и емкость C. Активные же элементы могут увеличивать энергию сигнала.
Все элементы радиоэлектронных цепей, кроме того, подразделяются на элементы с сосредоточенными и распределенными параметрами.
Если линейные размеры элементов намного меньше длины волны
действующего в цепи сигнала, то они являются элементами с сосредоточенными параметрами. В противном случае мы имеем дело с элементами с распределенными параметрами.
Электрические цепи можно разделить на два больших класса: линейные и нелинейные. Цепь называется линейной, если ее параметры
не зависят от приложенного напряжения и протекающего в ней тока.
Очень часто какую-либо линейную или нелинейную электрическую цепь, составленную из пассивных
I1
I2
и активных элементов, удобно рассмат1
3
ривать в виде четырехполюсника, имеU2 ющего четыре доступных вывода
U1
(рис. 2.1). Два из них при этом образу4
2
ют вход данной цепи, а два других –
выход. К входным выводам может подРис. 2.1. Электрическая цепь,
представленная в виде четыключаться источник сигнала, а к вырехполюсника
ходным – нагрузка.
2.1. Основные свойства линейных цепей
Свойство 1. Процессы в линейных цепях описываются линейными
дифференциальными уравнениями с постоянными коэффициентами.
Приведем пример такой цепи. Если имеется простая последовательная цепь, состоящая из сосредоточенных пассивных элементов, а
именно сопротивления R, индуктивности L и емкости C, а также источника эдс e(t) (рис. 2.2), то процессы в ней описываются следуюdi
щим
интегродифференциальным
уравнением
L 
dt
20
L
1
 idt et  , так как
C
напряжения на сопротивлении,
индуктивности и емкости соответственно равны UR  Ri ,
di
1
и UC   idt . После
UL  L
dt
C
дифференцирования обеих частей этого уравнения получим
 Ri 
e(t)
~
R
C
Рис. 2.2. Электрическая цепь,
состоящая из элементов с сосредоточенными параметрами
и источника эдс
d 2i
di 1
d
(2.1)

R

i

et ,
dt C
dt
dt 2
что соответствует сформулированному выше свойству.
Известно, что систему из n дифференциальных уравнений первого
порядка можно заменить одним дифференциальным уравнением n-го
порядка. В силу этого, для сложной цепи, состоящей из n простых цепей, справедливо уравнение
L
d ni
d n 1i
di
(2.2)

a



a
 a0i  f t ,
n

1
1
dt
dt n
dt n 1
где f(t) – некоторое внешнее воздействие.
Если в уравнении (2.2) все коэффициенты an являются постоянными, то это уравнение описывает линейную систему с постоянными параметрами.
Если хотя бы один из коэффициентов an является функцией времени, то уравнение (2.2) будет характеризовать систему с переменными
параметрами или параметрическую цепь.
Если хотя бы один из коэффициентов an является функцией тока
(или напряжения, если уравнение записано относительно переменной
u), то мы будем иметь нелинейную систему.
Свойство линейности элементов можно истолковать как результат
линейности их вольтамперных характеристик на определенной частоте (=const).
Свойство 2. Для линейных цепей справедлив принцип независимости при наложении внешних воздействий или, другими словами,
принцип суперпозиции.
Этот принцип можно проиллюстрировать следующим образом. Если к линейной системе приложить несколько внешних воздействий
an
21
fi(t), где i=1, 2, 3, …, то поведение такой системы можно описать путем наложения (суперпозиции) решений, найденных для каждого из
воздействий в отдельности. Для простоты рассмотрим цепь, которая
при заданном значении f1(t) описывается простым уравнением
dy
(2.3)
 a0 y  f1 t  ,
dt
а решением этого уравнения является некоторая функция y1(t), где под
y(t) понимается величина тока, напряжения или заряда.
При приложении к этой же системе воздействия f2(t) процессы в ней
будут описываться уравнением
a1
dy
(2.4)
 a0 y  f 2 t  ,
dt
а его решением будет функция y2(t).
При одновременном действии на систему двух воздействий f1(t) и
f2(t) соответствующее уравнение будет иметь вид
a1
dy
 a0 y  f1 t   f 2 t .
dt
Решением его будет некоторая функция y3(t).
Если система линейна, то должно выполняться соотношение
a1
y3(t)=y1(t)+y2(t).
(2.5)
(2.6)
Если же система нелинейна, то
y3(t)y1(t)+y2(t).
(2.7)
Свойство 3. В линейных системах не происходит преобразования
спектра частот.
Это свойство является следствием того, что операции интегрирования и дифференцирования являются линейными. Так для цепи, изображенной на рис. 2.2, воздействие f(t)=е(t) будет описываться тремя
слагаемыми, линейно связанными протекающими по цепи токами с
падениями напряжений на резисторе, индуктивности и емкости. Тогда, если, например,
it   I sin t ,
то
U R  RI sin t ,
22
(2.8)
UL  L
d
it   LI cost ,
dt
(2.9)
1
1
it dt  
I cost .
(2.10)

C
C
В случае сложного характера функции f(t), последняя разлагается на
элементарные составляющие в ряд Фурье, и на основании вышеизложенного каждая из составляющих даст реi
шение с одной и той же постоянной частоi3
той.
i2
С другой стороны, в нелинейных цепях, ко- i
1
торые будут рассмотрены в четвертой главе
курса, всегда происходит преобразование спектра частот сигнала. Это же утверждение спраu1 u2
u3 u
ведливо и для параметрических цепей. При
Рис. 2.3. Зависимость тока
этом в нелинейной системе структура преоб- сигнала от его амплитуды
разованного сигнала зависит не только от
для некоторой нелинейвремени, но и от амплитуды. Если, наприной системы
мер, u3=u1+u2, то i3i1+i2 (рис. 2.3).
UC 
2.2. Дифференцирующие цепи
С помощью простейших RC- и RL-цепей (рис. 2.4) можно проводить
дифференцирование сигналов.
Пусть на вход RC-цепи (рис. 2.4 а) подан сигнал Uвх. Тогда
1
UС  UR  Uвх , но UС   idt , а UR=Ri и, следовательно,
C
1
U вх   idt  Ri .
(2.11)
C
Умножая числитель и знаменатель первого слагаемого в правой части уравнения (2.11) на R и учитывая, что напряжение на выходе
Uвых=UR, получим
23
С
Uвх
R
Uвых
R
Uвх
а
L
Uвых
б
Рис. 2.4. Дифференцирующие цепи: а – RC-цепь, б – RL-цепь
U вх 
1
U вых dt  U вых .
RC 
(2.12)
Обозначая далее постоянную времени данной цепи RC=, а затем
дифференцируя обе части уравнения (2.12) по времени t, получим
dU вх 1
dU вых
.
(2.13)
 U вых 
dt

dt
dU вых
1
При условии, что
 U вых , (это справедливо, когда  достаdt

точно мала), на основании равенства (2.13) будем иметь
dU вх
,
(2.14)
dt
из чего следует, что выходное напряжение пропорционально производной от входного, т. е. имеет место операция дифференцирования
входного сигнала.
1
Если положить, что  очень велика и значением U вых по сравне
dU вых
нию с величиной
можно пренебречь, то на основании соотноdt
dU вх dU вых
шения (2.13) получим
, откуда Uвых=Uвх, и RC-цепь в

dt
dt
этих условиях становится переходной, т. е. такой цепью, проходя через которую сигнал на ее выходе повторяет входной. Эта цепь может
использоваться, например, для связи между отдельными каскадами
многокаскадного усилителя.
Из сказанного выше видно, что дифференцирование будет тем точнее, чем меньше постоянная времени цепи =RC. Но уменьшение постоянной времени , как следует из выражения (2.14), ведет к уменьшеU вых  
24
нию величины напряжения на выходе цепи, поэтому идеальное дифференцирование с ее помощью невозможно. Условием приближенного
дифференцирования, в частности, в случае прямоугольного импульса
будет неравенство <<tи, где tи – длительность дифференцируемого импульса.
Дифференцирующую цепь называют также обостряющей или укорачивающей, так как длительность выходных импульсов меньше длительности входных, а их вершина является острой (см. рис. 2.7). Как
видно из этого рисунка, при определении длительности продифференцированных импульсов появляется некоторая неопределенность. Если
же длительность импульса определять на уровне 0,5Um, где Um – его
tи

амплитуда, то справедливо равенство 0,5U m  U me 0,5 , откуда
ln 0,5   tи0,5  , и тогда длительность импульса по уровню 0,5 будет
равна
tи 0 ,5  0,7.
(2.15)
Формула (2.15) может быть использована при экспериментальном
определении постоянной времени  цепи.
Выражение для комплексного коэффициента передачи дифференцирующей цепи, изображенной на рис. 2.4 а, имеет вид
U вых
R
jRC

K



1
U вх
1

j

RC
R
j C
2
RC   j RC  a  jb.

(2.16)
1  RC 2
1  RC 2
При этом модуль коэффициента передачи рассматриваемой цепи или,
другими словами, ее амплитудно-частотная характеристика (АЧХ)
выразится как
K  a 2  b2 
 RC
1  ( RC )
2


1  ( )
2

2 fRC
1  (2 fRC ) 2
.
(2.17)
Фазовый сдвиг между напряжением на входе и выходным напряжением или фазо-частотная характеристика (ФЧХ) дифференцирующей
цепи определяется формулой
b
1
1
.
  arctg  arctg
 arctg
(2.18)
a
RC
2fRC
25
K
1

/2
f
f
а
б
Рис. 2.5. Частотные характеристики дифференцирующей цепи:
а – АЧХ; б – ФЧХ
Аналогичными характеристиками обладает и RL-цепь, изображенная на рис. 2.4 б, постоянная времени которой =L/R. Графики функций (2.17) и (2.18) представлены на рис. 2.5.
Если на вход дифференцирующей цепи подать единичный скачок
напряжения Uвх(t)=(t) (рис. 2.6 а), то в этом случае можно получить
так называемую переходную характеристику h(t) (рис. 2.6 б) этой цепи, представляющую собой зависимость сигнала на выходе цепи при
единичном скачке напряжения на ее входе
U вых t   ht   e t  .
(2.19)
При воздействии на дифференцирующую цепь сигнала прямоугольной формы на выходе получается напряжение, частный случай
которого представлен на рис. 2.7. Вид напряжения на выходе определяется постоянной времени =RC.
Uвх(t)
Uвх(t)=(t)
Uвых(t)=h(t)
1
Um
1
Uвых(t)
Um
1
e
0
t
0

t
а
б
Рис. 2.6. Отклик дифференцирующей
цепи на единичный скачок напряжения: а – единичный скачок напряжения; б – переходная характеристика
26
а
tи
t
б
t
Рис. 2.7. Дифференцирование прямоугольного импульса: а – вид импульса
до дифференцирования; б – продифференцированный импульс
2.3. Интегрирующие цепи
На рис. 2.8 изображены простейшие RC- и RL-интегрирующие цепи.
Рассмотрим цепь, изображенную на рис. 2.8 а. В данном случае выходной сигнал снимается с емкости и уравнение, описывающее расL
R
Uвх
С
Uвых
Uвх
а
R
Uвых
б
Рис. 2.8. Интегрирующие цепи: а – RC-цепь; б – RL-цепь
сматриваемую цепь Uвх=Ri+Uвых, можно представить в виде
dU
U вх   вых  U вых .
(2.20)
dt
dU
Пусть в равенстве (2.20)  велика так, что  вых  U вых . Тогда буdt
dU
дем иметь U вх   вых , откуда
dt
1
(2.21)
U вых  U вх dt ,

т. е. выходное напряжение пропорционально интегралу от входного, и
поэтому с помощью данной цепи может выполняться операция интегрирования.
Если же в равенстве (2.20) положить, что  мала, и имеет место соdU
отношение  вых  U вых , то можем записать, что
dt
U вых  U вх .
(2.22)
В этих условиях цепь называется переходной, т. к. выходной сигнал
повторяет входной.
Как следует из выражения (2.20), интегрирование происходит тем
точнее, чем больше постоянная времени . Но увеличение постоянной
времени =RC, как видно из выражения (2.21), ведет к уменьшению
величины выходного напряжения, поэтому идеально точное интегрирование с помощью рассмотренной выше цепи невозможно. В случае,
27
например, приближенного интегрирования прямоугольного импульса
должно выполняться неравенство tи<<.
Комплексный коэффициент передачи напряжения интегрирующей
RC-цепи (рис. 2.8 а) можно представить в виде
U
K  вых
U вх
1
1
RC
jC



j
 a  jb.
2
2
1




1  RC
1  RC
R
jC
(2.23)
АЧХ цепи будет иметь вид
K  a2  b2 
1
1  RC 
2

1
1  2fRC 
2

1
1   
2
ФЧХ цепи определяется выражением
  arctg  RC   arctg  2fRC   arctg  2f  .
.
(2.24)
(2.25)
Графики функций (2.24) и (2.25) представлены на рис. 2.9.
Аналогичными свойствами обладает и RL-цепь с постоянной времени =L/R, изображенная на рис. 2.8 б.
Переходная характеристика интегрирующей цепи получается интегрированием выражения (2.20) при Uвх=(t) и имеет вид:
(2.26)
U вых t   ht   1  e t  .
Пример интегрирования прямоугольного импульса представлен на
рис. 2.10. Форма напряжения на выходе интегрирующей цепи определяется, как и в случае дифференцирующей цепи, постоянной времени .
K
1
Uвх(t)
Um
а
tи
а
t
f
Uвых(t)
Um
f
б
б
–/2
–
Рис. 2.9. Частотные характеристики интегрирующей
цепи: а – АЧХ; б – ФЧХ
t
Рис. 2.10. Прямоугольный импульс: а – до интегрирования;
б – после интегрирования
28
2.4. Колебательные контуры.
Свободные колебания в контуре
В различных радиотехнических устройствах, в частности, в радиоприемных, одной из важнейших операций является выделение полезного сигнала из всевозможных побочных сигналов и помех. Эти
функции выполняются электрическими колебательными системами,
основным элементом которых является колебательный контур. При
изучении свойств колебательного контура главное внимание обращается на его резонансные свойства, которые и определяют его частотную избирательность. В зависимости от способа включения элементов
колебательного контура индуктивности L и емкости С по отношению
к внешнему источнику возбуждения различают последовательный и
параллельный колебательные контуры.
При отсутствии внешнего возбуждения в колебательном контуре с
первоначально запасенной энергией электрического поля в конденсаторе или магнитного поля в индуктивности возможно существование
свободных колебаний.
Рассмотрим переходные процессы в цепи, состоящей из индуктивности L, емкости C и активного сопротивления R (рис. 2.11). Если
предварительно зарядить конденсатор C, а затем в начальный момент
времени t=0 замкнуть его на цепь, состоящую из последовательно
включенных элементов L и R, то в таком контуре будет идти процесс
периодического преобразования электрической энергии в магнитную
и наоборот. В этом случае функция, описывающая внешнее воздействие при любых t 0, равна нулю и
R
уравнение Кирхгофа для такой цепи
имеет вид
K
di 1
(2.27)
Ri  L   idt  0 .
E +
С
L
dt C
После дифференцирования обеих частей
соотношения (2.27) по времени и деления на L приходим к следующему дифференциальному уравнению для тока в
контуре
Рис. 2.11. Схема для заряd 2i R di 1


i  0.
dt 2 L dt LC
(2.28)
29
да и разряда конденсатора
колебательного контура
Введем следующие параметры:
1
1
R
или f 0 
.

, 0 
(2.29)
2L
LC
2 LC
Тогда с учетом соотношений (2.29) уравнение (2.28) принимает вид
d 2i
2
 2
di
 02i  0 .
dt
(2.30)
dt
Решение этого дифференциального уравнения будем искать в виде
(2.31)
I t   Ze t ,
где Z – некоторая новая переменная. Подстановка решения (2.31) в
(2.30) приводит к следующему уравнению:
d 2Z
dt
2


 0 2   2 Z  0.
(2.32)
02   2  .
(2.33)
Обозначим
С учетом обозначения (2.33) дифференциальное уравнение (2.32) принимает вид
d 2Z
(2.34)
 2 Z  0.
2
dt
Как известно, решением колебательного уравнения (2.34) является
функция вида
(2.35)
Z  I m cos t   .
После подстановки этого решения в выражение (2.31) для тока І получим окончательно
(2.36)
I t   I m e  t cos t  .
Из уравнения (2.36) следует, что ток в колебательном контуре изменяется по гармоническому закону, причем его амплитуда с течением времени непрерывно уменьшается. Затухание амплитуды тока аналитически описывается множителем e-t. Скорость затухания собственных колебаний в контуре можно охарактеризовать отношением
амплитуд тока в некоторые моменты времени t1 и t1+T, отстоящих
друг от друга на период колебаний Т (рис. 2.12).
30
Используя формулу
находим это отношение
(2.36),
Ime-t
I
I(t)
it1 
e  t1
   t T   e T . (2.37)
it1  T  e 1
Натуральный логарифм выражения (2.37) носит название логарифмического декремента затухания контура, и для контура с
малыми потерями будет иметь
вид
R
R
  Т  
  , (2.38)

LC
t1
t1+T
I(t+T)
t
Рис. 2.12. Форма свободных колебаний в контуре
где   L C – волновое или характеристическое сопротивление
контура.
На практике вместо логарифмического декремента затухания (2.38)
часто используется пропорциональная ему величина – затухание d
 R 1
(2.39)
d   ,
  Q
где параметр Q, равный
(2.40)
Q=/R,
называется добротностью контура.
С энергетической точки зрения добротность контура характеризует
отношение запасенной электромагнитной энергии контура при резонансе к средней энергии, теряемой в этом режиме на активном сопротивлении контура за один период изменения тока.
Добротность Q контура с малым затуханием можно оценить путем
подсчета по осциллограмме числа периодов свободных колебаний в
контуре m за интервал времени, в течение которого амплитуда собственных колебаний контура уменьшается, например, в два раза. Тоe  t1
гда согласно соотношению (2.37)   t  mT   2, или emТ=2, откуда
e 1
mТ=ln2. При этом логарифмический декремент затухания  на основании формулы (2.38) будет равен =T=ln2/m, а затухание d выразится как d=/=ln2/m. Отсюда добротность контура будет равна
1 m
(2.41)
Q 
 4,53m .
d ln 2
31
2.5. Последовательный колебательный контур
Последовательный колебательный контур (рис. 2.13) образуется
при последовательном включении емкости C, индуктивности L и генератора эдс e(t). Обычно для учета всех активных потерь в контуре
на схемах включают эквивалентное сопроL
тивление R. Будем считать в дальнейшем
R
эдс гармонической, а внутреннее сопроC
e(t)
тивление генератора Ri=0. В этом случае
все частотные характеристики контура
называются предельными. Влияние внутРис. 2.13. Схема последовареннего сопротивления источника эдс на
тельного колебательного
параметры контура будет рассмотрено доконтура
полнительно.
Для цепи, изображенной на рис. 2.13, можно записать уравнение
Кирхгофа в комплексном виде
1
,
E  IR  IjL  I
(2.42)
jC
где E  E m e j t E   E me jt , I  I me j t I   Ime jt . Здесь Em и Im –
амплитуды, E m и Im – комплексные амплитуды, соответственно эдс и
тока. Тогда согласно методу комплексных амплитуд на основании
(2.42) получим
E m
E m
Im 

.
(2.43)
1  Z  j

R  j  L 

C 

В выражении (2.43)
1 

Z  j  R  j L 
(2.44)
  R  jX

C


называют комплексным входным сопротивлением, в котором величина
1
(2.45)
X  L 
C
является его реактивной составляющей. ФЧХ контура при этом определяется зависимостью
1
L 
(2.46)
X
C .
  arctg  arctg
R
R
32
ХL, –XC,
XL+(–XC)
1
0
о
3

2
Рис. 2.14. Зависимость сопротивлений колебательного контура от частоты: 1 – индуктивного ХL; 2 – емкостного (–XC);
3 – полного реактивного X=XL+(–XC)
Рассмотрим зависимость входного сопротивления последовательного колебательного контура Z  j от частоты генератора. На
рис. 2.14 построены зависимости ХL=L и –ХC= –1/C, а также
X=XL+(–XC) как функции частоты генератора . Как видно из рисунка, характер сопротивления контура определяется соотношением
между ХL и ХC. Так, для частот <0 выполняется неравенство XL<XC,
и характер сопротивления контура емкостный, а при >0 – неравенство ХL>ХC, и характер сопротивления контура индуктивный. С практической точки зрения случай =0, когда XL=XC, представляет
наибольший интерес, поскольку соответствует условию резонанса.
1
1
Итак, при резонансе Х=0 или 0 L 
.
 0, отсюда 0 
0 C
LC
Амплитуда тока при резонансе достигает максимума и равна I0=Em/R.
Напряжения на реактивных элементах L и C соответственно имеют
E
E

1
значения U Lрез  j m 0 L  jEm  jQEm , и U Cрез  m

R j0C
R
R

  jEm   jQEm , т. е. напряжения на индуктивности и емкости при
R
резонансе в последовательном колебательном контуре равны по модулю, сдвинуты по фазе на  и в Q раз больше, чем эдс источника.
Преобразуем реактивную составляющую входного сопротивления
последовательного контура с учетом того, что 0L= и 0= 1/ LC .
Тогда
 
  0 
1
1 
   
 ,
(2.47)
X  L 
 0 L 


C



LC


0
 0

 0

а выражение для тангенса сдвига фаз на основании (2.46) имеет вид
33
  0 
X
(2.48)
   .
 Q 

R
 0  
Введенный здесь параметр  называется обобщенной расстройкой.
На практике наибольший интерес представляют характеристики
контура в области частот, близких к резонансной частоте 0. В этом
 0  
случае справедливо приближенное равенство

 1, где
0
0
 – абсолютная расстройка. Для области малых абсолютных расстроек выражения (2.47) и (2.48) принимают вид
tg 
X 
2  02

2
02

tg    Q
  0   0 

2
2  02

2
02
02
 2Q
 2

,
0
(2.49)

,
0
(2.50)
и тогда модуль входного сопротивления контура Z() будет равен
Z  R 2  X 2  R 1   2 .
(2.51)
На рис. 2.15 приведены графики зависимости от величины относительной
расстройки 0 входного сопротивления контура Z() и его фазовой
характеристики ()=arctg 2Q0.
Нормированную частотную зависимость (резонансную характеристику или резонансную кривую) тока в цепи последовательного колебательного контура можно получить делением величины Im на I0, и с
Zвх

/2

0
R

0
-/2
а
б
Рис. 2.15. Зависимость сопротивления последовательного контура от
относительной расстройки /0 (а) и его фазовая характеристика (б)
34
учетом вышеизложенного эта зависимость будет иметь вид
Im
Em
1



2
I 0 Z I 0
1 
1
2

1
2
.
(2.52)

 0 
 


1  Q 

1   2Q



0 
 0


На рис. 2.16 показано семейство кривых (2.52) при разных значениях параметра Q, в случае, когда Q1>Q2>Q3.
Найдем связь между полосой пропускания последовательного контура и его добротностью. Полагая, что ординаты резонансной характеристики контура на границах его полосы пропускания уменьшаются
в 2 раз по сравнению с их значением при резонансе, приходим к
следующему простому соотношению:
1
1
,

2
2
(2.53)
 

1   2Q

 

2
где 2 или 2f – полоса пропускания контура, откуда
2 2f
1

d  .
0
f0
Q
В реальных схемах сопротивление источника сигнала Ri 0, поэтому на эквивалентных схемах такой источник обычно заменяют генератором с эдс e(t) и внутренним сопротивлением Ri. В этом случае
схема последовательного контура принимает вид, представленный на
рис. 2.17. Эквивалентная добротность такого контура

Q
Qэ 

.
(2.54)
Ri
R  Ri
1
R
Соответственно этому уравнение резонансной кривой нормированного тока такого контура принимает следующий вид:
Im

I0
1

 

1   2Qэ
o 

2
.
(2.55)
Сравнительный анализ выражений (2.54) и (2.40), а также (2.55) и
(2.52) показывает, что различие между ними уменьшается, если Ri0.
35
Im
I0
1
1
2
Ri
Q1
н
0
0
в
0
L
Q3
Q2
С

0
e(t)

R R
2
0
Рис. 2.16. Резонансная характеристика последовательного контура
при различных значениях его добротности Q
По
ло
са
Рис. 2.17. Схема
последовательпр
ного колебательного
контура с
озр
ач у которого Ri0
генератором эдс,
но
ст
контур обладаетинаилучшими ре-
Это означает, что последовательный
зонансными свойствами в том случае, если Ri<<R. K(
)
2.6. Параллельный колебательный контур
1/
2 цепь, состояПараллельным колебательным контуром называется
1
щая из параллельно включенных индуктивности L, емкости
C и генес
ратора эдс. Если заменить индуктивность L и емкость
 C соответству-
ющими эквивалентными элементами, состоящими изПопоследовательно
ло
включенных L и rL для индуктивности и C и rC для саконденсатора, то
пр
приходим к схеме параллельного контура, представленной
на
озр
ач предварительрис. 2.18. Рассмотрим
но
но предельные характеристики
такост
L
С
и
го параллельного контура. Они реаRi
лизуются, если к контуру подклюrL
rC
чить источник тока с внутренним соe(t)
IL
IC
противлением Ri.
в Влияние велиI
чины Ri на параметры контура будет
Рис. 2.18. Схема параллельного проанализировано ниже.
колебательного контура с учетом
Для входного сопротивления конактивных сопротивлений индуктура запишем очевидное равенство
тивности и емкости
36
г
Ри
с.
2.
23
.
Ча
ст
 jL  rL 

1
L

 rС 
  rL rC  rL  rC 
 jC
  C

Z пар  j 

2
1 

1


2
rL  rС  j  L 
 rL  rC    L 

C 

C 

(2.56)
rL 
1 
L
1 

2
2 1
rC L  rL
  L 
 LrC 
 L 


C 
C 
C C 
C 


j
.
2
2
rL  rC 2   L  1 
rL  rC 2   L  1 
C 
C 


Резонансную частоту можно найти, если приравнять к нулю мнимую
часть выражения (2.56), а именно ее числитель
1
L
1 
  p L 
 0.
pC C 
pC 
Тогда решение уравнения (2.57) относительно p дает
rC 2 p L  rL 2
p 
С учетом того, что
rL 2С  L
2
2
2
rC C L  L C
1
 0 , а
LC

1
LC
rL2C
1
L
.
rС2C
1
L
(2.57)
(2.58)
L
  , соотношение (2.58) приниC
мает вид:
р  0
 2  rL2
.
 2 r C2
(2.59)
Простейший анализ выражения (2.59) приводит к следующим выводам.
1. Если rL=rC=0 или rL=rC 0, то р=0, т. е. резонансная частота параллельного контура совпадает с резонансной частотой последовательного контура, состоящего из идентичных параллельному элементов.
2. Если rL>rC или rC=0, то р<0, а при rL<rC или rL=0, р>0. Таким образом, р в зависимости от соотношения между rL и rC может
быть как больше, так и меньше 0.
Рассмотрим зависимость входного сопротивления параллельного
колебательного контура от частоты генератора. С учетом того что, как
37
правило, rL<<L, и rC<<1/C, выражение (2.56) можно упростить и
привести его к виду
L
2
2
C


(2.60)
Z  j  Z вх пар 


,
1  Z вх R1  j 

R  j  L 

C 

где R=rL+rC, а Z
и Z вх – входные сопротивления параллельного
вх пар
и последовательного контуров соответственно. Как следует из соотношений (2.44) и (2.60),
(2.61)
Z вх пар Z вх =2.
Формула (2.61) позволяет сделать вывод о том, что последовательный
и параллельный контуры, составленные из одинаковых элементов, являются обратными со стороны входных клемм.
Если частота генератора сопадает с резонансной частотой 0, то
=0, и тогда величина Z вх пар будет равна
02 L2
2
1


Z вх пар  Z вх рез  Rрез 
 Q 
 2 2 .
R
R
0 C R
(2.62)
Выражение (2.60) с учетом соотношения (2.62) можно переписать в виде
Rрез
Rрез
Rрез
2
(2.63)



j
 Rвх пар  jX вх пар ,
R1  j  1  j 1   2
1  2
где активная и реактивная составляющие входного сопротивления
контура соответственно равны
Z вх пар 
Rвх пар 
и
Rрез
1 
X вх пар  
(2.64)
2
Rрез
1  2
(2.65)
,
а его модуль
Z вх пар 
Rрез
1 
2

Rрез

 

1   2Q

0 

38
2
.
(2.66)
Нормированное входное сопротивление параллельного контура
находится делением величины Zвх пар на величину Rрез. Тогда будем
иметь
Z вх пар
1
1


.
2
2
Rрез
(2.67)
1 

 

1   2Q
0 

Формула (2.67) представляет собой уравнение граничной резонансной
кривой входного сопротивления параллельного контура.
От частотной характеристики входного сопротивления параллельного контура можно перейти к частотной характеристике напряжения
на нем при условии питания контура неизменным током. В самом деле, комплексная амплитуда напряжения U на контуре равна
IRрез



(2.68)
U  IZ вх пар 
,
1  j
а отношение модуля этого напряжения к напряжению на контуре при
резонансе Upез=IRрез равно
Z вх пар
U
1


.
(2.69)
U рез
Rрез
1  2
Очевидно, что выражение (2.69) для резонансной кривой по напряжению совпадает с уравнением (2.67) резонансной кривой входного сопротивления параллельного контура.
Тангенс фазового сдвига для входного сопротивления параллельного контура на основании формул (2.64) и (2.65) равен
tg 
X вх пар
Rвх пар
  0 
 ,
   Q



 0

(2.70)
и для области малых расстроек количественно можно принять

(2.71)
  2Q
.
0
На рис. 2.19 приведены графики зависимости (2.66) для двух значений параметров Q (Q1>Q2) и зависимости (2.65), а также график зависимости фазового сдвига от относительной расстройки для параллельного контура в соответствии с соотношением (2.70).
39
Рассмотрим влияние внутреннего сопротивления генератора Ri на
избирательные свойства параллельного контура. Схема контура с генератором, у которого Ri, приведена на рис. 2.18. Амплитуда
.
будет равна U  I Z вх пар , где
напряжения в таком контуре
.
.
.
I
E
и тогда
R i  Z вх пар
E Z вх пар

U
 E
Ri  Z вх пар
Rрез
Rрез
nE
1  j
 E

,
Rрез
Ri  jRi  Rрез 1  j  n
Ri 
1  j
где n=Rрез/Ri.
Модуль величины U определяется формулой
nE
U
.
1  n 2  2
(2.72)
(2.73)
При резонансе =0 и выражение (2.73) принимает вид
nE
(2.74)
Up 
.
1 n
Нормированная резонансная кривая по напряжению параллельного
колебательного контура с учетом внутреннего сопротивления генераZвх пар
Хвх пар

/2
р
Q1 Q2
Rрез

0
0,5 Rрез

0
-/2
Xвх пар
а
б
Рис. 2.19. Частотные характеристики параллельного контура:
а – резонансная; б – фазовая
40
тора получается делением соотношения (2.73) на (2.74)
U
1 n
,

2
2
Up
1  n   
а с учетом соотношения (2.50) это отношение перепишется
U
1
1
1



,
2
2
Up
2



 
1



1   2Qэ
2


1

 Rрез 

0 

1   2Q
1 



R
0
Ri 
рез

1


R
i 

где эквивалентная добротность Qэ равна
1
.
Qэ 
Rрез
1
Ri
(2.75)
(2.76)
(2.77)
Проанализируем выражения (2.75) – (2.77).
1. Если Ri0, то n>>1 и U/Upconst. Значит, при Ri0 напряжение
на контуре не зависит от частоты (рис. 2.20, Ri=0).
2. При Ri, n<<1 и QэQ. Следовательно, при Ri резонансная
кривая приближается к предельной резонансной кривой (рис. 2.20,
Ri).
3. Некоторое промежуточное значение резонансной кривой при
0<Ri показано на рис. 2.20.
Проведенный анализ показывает, что избирательные свойства паU/Uрез
Ri=0
0<Ri<
Ri

0
Рис. 2.20. Зависимость отношения напряжений U/Uрез от
относительной расстройки для параллельного контура при
трех различных значениях внутреннего сопротивления
генератора
0
41
раллельного контура будут выражены более резко с увеличением
внутреннего сопротивления Ri генератора, питающего контур.
2.7. Связанные контуры
Простые контуры могут быть связаны между собой индуктивной, емкостной или резистивной связью. В данном разделе рассмотрим два
одиночных контура, связанных с помощью индуктивной или трансформаторной связи (рис. 2.21). Для характеристики степени связи в этом
.
E
>
R1
M
.
I1
L1
R2
L2
R1
.
I2
C2
.
Uвых
C1
Рис. 2.21. Два одиночных контура, связанных
трансформаторной связью
случае вводится коэффициент связи kсв, который выражается через коэффициент взаимной индукции M следующим образом:
M
k св 
,
(2.78)
L1 L2
где L1, L2 – индуктивности катушек первого и второго контура соответственно. Параметр М имеет размерность индуктивности и характеризует степень влияния тока I2 на величину эдс, наводимой в катушке первого контура и, наоборот, тока I1 на величину эдс, наводимой в
катушке второго контура.
На основании второго закона Кирхгофа для комплексных амплитуд
рассматриваемой схемы связанных контуров (рис. 2.21) можно записать следующую систему уравнений:


1  



R

j

L

 1
 1 C  I m1 jMI m 2  Em ,

1 



1  
 I m 2 jMIm1  0.
 R2  j  L2 

C

2 

42
(2.79)
Или, вводя комплексные сопротивления Z1 и Z 2 ,
Z1 Im1  jMIm 2  E ,
Z 2 Im 2  jMIm1  0.
(2.80)
Назовем сопротивлением связи произведение jM  Z св и перепишем систему (2.80) в виде
Z1 I m1 Z св Im 2  E ,
(2.81)
Z 2 I m 2 Z св Im1  0.
Отметим, что при согласованном включении катушек перед сопротивлением связи jM в формулах ставится знак «+», а при их встречном включении знак «–». При этом одноименные зажимы катушек
обозначаются символом «», как это показано на рис. 2.21.
Выразим из второго уравнения системы (2.81) ток Im 2 и подставим
Z I
его в первое уравнение. Тогда соответственно получим: I m 2  св m1
Z 2
 Z I 
и Z1 I m1 Z св   св m1   E m , откуда величина тока Im1 запишется слеZ 2 

2
Z св
E m
E m
, где 
 Z вн – вноси
2




Z
Z

Z
Z
2
1
вн
Z1  св
Z 2
мое сопротивление, которое в общем виде можно представить как
(2.82)
Z вн  Rвн  jX вн .
дующим образом: I m1
Таким образом, на основании вышеприведенных выкладок можно
сделать вывод о том, что, в частности, влияние второго контура на
первый сводится к изменению эквивалентного активного и реактивного сопротивлений последнего, а именно к:
1. увеличению его эквивалентного активного сопротивления на величину Rвн. Это увеличение обусловлено рассеянием части энергии источника на активном сопротивлении второго контура;
2. изменению его эквивалентного реактивного сопротивления на
величину Хвн. Это изменение связано с наводимой в данном контуре
эдс взаимной индукции.
Комплексный коэффициент передачи K , равный по определению
отношению напряжения на выходе всей цепи U m вых к напряжению генератора E m (см. рис. 2.21), можно представить в виде
43
U
Im 2
M
1
(2.83)
.
K  m 

E m E m jC2 C2 Z1Z 2  2 M 2
Для упрощения анализа и дальнейших вычислений будем считать,
что оба контура имеют равные по величине номинальные значения
элементов R, L и C и в соответствии с этим равные собственные резонансные частоты р1=р2=0. Тогда в достаточно узкой полосе частот
 справедливо соотношение L0L=.
Используя формулы, связывающие добротность контура Q с затуханием d: Q=1/d=/R, а также реактивную составляющую входного
сопротивления X с характеристическим сопротивлением  и относительной расстройкой : X==2/0, так что =2/0, приведем
формулу (2.83) к виду
M
1
1
K 
 k св 2 2

2
2
2
2 2
C Z  M
R  j 2 RX  X 2  k св

k св
2
(2.84)
k св

.
2 2
2
R 2  j 2 RX   2  2  k св

d 2  k св
  2  j 2 d
На основании этого выражения можно получить АЧХ связанных
контуров
K   K  K 
d
kсв


2 2
kсв
2
2
2
kсв

.
2
4
(2.85)

8d 
  16
Для дальнейшего анализа определим ее экстремальные точки, приdK
равняв к 0 производную
. Таким образом, для определения эксd
тремальных
точек
будем
иметь
следующее
уравнение

 
2

2
2
 8 d 2  k св
 2  16 4
dK d 2  k св

 0 , решение которого дает таd
d
кие значения переменной :
2
2
k св
 d2
 k св
d2
(2.86)
1=0,  2 
, 3 
.
2
2
Так как согласно точному определению относительная расстройка
 0  2


 1, откуда   0 1   ; при малых расстройравна  
0  02
ках имеет место приближенное равенство
(2.87)
  0 1   .
44
45