Исходные данные.
реклама
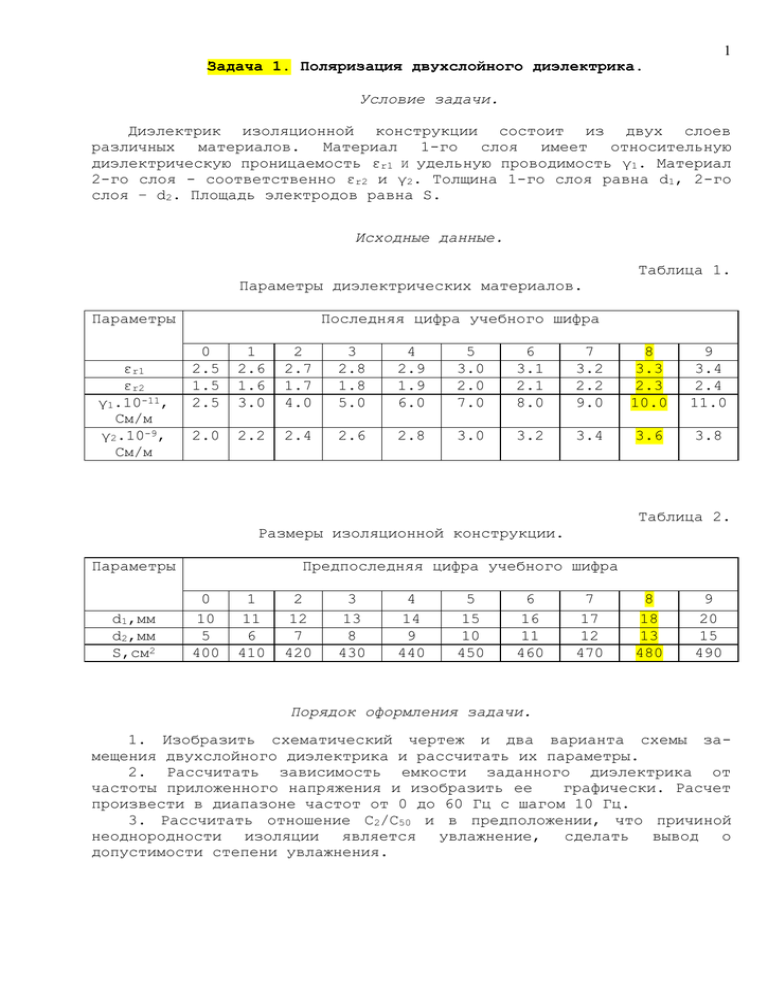
1 Задача 1. Поляризация двухслойного диэлектрика. Условие задачи. Диэлектрик изоляционной конструкции состоит из двух слоев различных материалов. Материал 1-го слоя имеет относительную диэлектрическую проницаемость εr1 И удельную проводимость γ1. Материал 2-го слоя - соответственно εr2 и γ2. Толщина 1-го слоя равна d1, 2-го слоя – d2. Площадь электродов равна S. Исходные данные. Таблица 1. Параметры диэлектрических материалов. Параметры εr1 εr2 γ1.10-11, См/м γ2.10-9, См/м Последняя цифра учебного шифра 0 2.5 1.5 2.5 1 2.6 1.6 3.0 2 2.7 1.7 4.0 3 2.8 1.8 5.0 4 2.9 1.9 6.0 5 3.0 2.0 7.0 6 3.1 2.1 8.0 7 3.2 2.2 9.0 8 3.3 2.3 10.0 9 3.4 2.4 11.0 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 Таблица 2. Размеры изоляционной конструкции. Параметры d1,мм d2,мм S,см2 Предпоследняя цифра учебного шифра 0 10 5 400 1 11 6 410 2 12 7 420 3 13 8 430 4 14 9 440 5 15 10 450 6 16 11 460 7 17 12 470 8 18 13 480 9 20 15 490 Порядок оформления задачи. 1. Изобразить схематический чертеж и два варианта схемы замещения двухслойного диэлектрика и рассчитать их параметры. 2. Рассчитать зависимость емкости заданного диэлектрика от частоты приложенного напряжения и изобразить ее графически. Расчет произвести в диапазоне частот от 0 до 60 Гц с шагом 10 Гц. 3. Рассчитать отношение С2/С50 и в предположении, что причиной неоднородности изоляции является увлажнение, сделать вывод о допустимости степени увлажнения. 2 Методические указания к решению задачи. В данной задаче рассматриваются некоторые особенности процесса поляризации неоднородных диэлектриков. Эти особенности имеют место в изоляции конструкций высокого напряжения, в которой обычно используются неоднородные диэлектрические материалы или комбинации диэлектриков. Кроме того, параметры рассматриваемых процессов используются при контроле качества однородной изоляции (например, ее местного увлажнения). Это определяет практическое значение данной задачи. Характерный для любого диэлектрика процесс поляризации заключается в ограниченном смещении связанных зарядов или ориентации дипольных молекул при воздействии на диэлектрик электрического поля. Процесс поляризации обратим: при снятии электрического поля диэлектрик из поляризованного состояния возвращается в обычное, неполяризованное состояние. Существует несколько видов поляризации, некоторые из которых сопровождаются рассеянием энергии и вызывают нагрев диэлектрика. Во всех случаях процессы поляризации протекают во времени. В некоторых случаях это время так мало (порядка 10-15 – 10-13 с), что их можно считать практически мгновенными. Другие виды поляризации развиваются значительно медленнее, их время может достигать десятков секунд. Количественно поляризация диэлектрика характеризуется его относительной диэлектрической проницаемостью εr которую в технике для краткости называют просто диэлектрической проницаемостью. Эта величина представляет собой отношение заряда на конденсаторе, содержащем данный диэлектрик, к заряду на конденсаторе при том же напряжении, если бы между электродами находился вакуум. Все виды поляризации можно разделить на две группы: 1) поляризация практически мгновенная и без рассеяния энергии (упругая); 2) поляризация замедленная и сопровождаемая рассеянием энергии в диэлектрике, то есть его нагреванием. Такую поляризацию называют релаксационной. К первой группе относятся электронная и ионная поляризации. Электронная поляризация представляет собой упругое смещение и деформацию электронных оболочек атомов и ионов. Время установления электронной поляризации - около 10-15 с, она характерна для всех диэлектриков. Ионная поляризация характерна для твердых диэлектриков с ионным строением и обусловливается смещением упругосвязанных ионов. Время ее установления - около 10-13 с. Рассмотрим виды поляризации, относящиеся ко второй группе. Дипольно-релаксационная поляризация возможна у веществ с дипольными молекулами и представляет собой их частичную ориентацию под действием электрического поля. Потери энергии при этом виде поляризации связаны с тем, что поворот дипольных молекул в вязкой среде требует преодоления некоторого сопротивления. Ионно-релаксационная поляризация имеет место в ионных кристаллических неорганических веществах с неплотной упаковкой ионов, она связана со смещением слабо связанных ионов вещества под действием электрического поля. Электронно-релаксационная поляризация возникает вследствие возбуждения тепловой энергией избыточных электронов или дырок. 3 Кроме перечисленных существует дополнительный вид поляризации, проявляющийся в твердых телах неоднородной структуры – так называемая миграционная поляризация. Эта поляризация связана с перемещением свободных зарядов (электронов и ионов) в пределах слоев и включений диэлектрических конструкций. Количественный расчет ряда параметров, связанных с миграционной поляризацией для конкретной диэлектрической конструкции и является предметом данной задачи расчетно-графической работы. Для полноты классификации видов поляризации следует упомянуть о спонтанной (самопроизвольной) поляризации, имеющей место у сегнетоэлектриков. В сегнетоэлектриках имеются отдельные области (домены), обладающие электрическим моментом в отсутствие внешнего поля. Этот вид поляризации связан с ориентацией электрических моментов доменов в направлении внешнего поля. Сегнетоэлектрики характеризуются очень высокой величиной диэлектрической проницаемости. Рассмотрим сущность миграционной поляризации на примере двухслойного диэлектрика, расположенного между плоскими электродами (рис. 1). Первый слой имеет толщину d1, диэлектрическая проницаемость его материала равна εr1, удельная проводимость – γ1. Для второго слоя эти параметры равны соответственно d2, εr2 и γ2. Рис.1. Двухслойный диэлектрик. Для такого диэлектрика возможны две схемы замещения, показанные на рис.2. Первая из них (рис.2а) - схема замещения по слоям. Ее элементы через параметры слоев можно выразить следующим образом: R1=(1/γ1)(d1/S); R2=(1/γ2)(d2/S); C1=ε0εr1(S/d1); C2=ε0εr2(S/d2), где S – площадь электродов; ε0=8,85.10-12 Ф/м – электрическая постоянная. 4 а) б) Рис.2. Схемы замещения двухслойного диэлектрика. Вторая схема замещения (рис. 2б) состоит из элементов, характеризующих двухслойный диэлектрик в целом. На этой схеме R – сопротивление утечки, характеризующее проводимость двухслойного диэлектрика в установившемся режиме, Сr – так называемая геометрическая емкость диэлектрика, определяемая только размерами и диэлектрическими проницаемостями его слоев и в которой не учитывается влияние процессов проводимости. Выражения для этих параметров очевидны: R=R1+R2; Cr=(C1C2)/(C1+C2). Два остальных параметра второй схемы можно определить из условия равенства полных сопротивлений диэлектрика в обеих схемах замещения: r=R1R2(R1+R2)(C1+C2)2/(R1C1-R2C2)2; ∆C=(R1C1-R2C2)2/[(R1+R2)2(C1+C2)]. При длительном приложении к двухслойному диэлектрику постоянного напряжения вследствие наличия проводимости на границе слоев будет накапливаться заряд абсорбции. Образование этого заряда и является следствием миграционной поляризации. Определим величину заряда абсорбции. Если к диэлектрику прикладывается напряжение величиной U0, то на первом и втором слоях будут устанавливаться напряжения соответственно: U1=U0(R1/(R1+R2)); U2=U0(R2/(R1+R2)). На емкостях слоев С1 и С2 накапливаются заряды: q1=U1C1=U0(R1C1/(R1+R2)); q2=U2C2=U0(R2C2/(R1+R2)). 5 При этом на границе абсорбции) будет равен: раздела слоев суммарный заряд (заряд │qабс│=│q1-q2│=U0│R1C1-R2C2│/(R1+R2). Из этого выражения следует, что заряд абсорбции будет существовать, то есть будет иметь место миграционная поляризация при условии: R1C1≠R2C2 или ε1/γ1≠ε2/γ2. Это и есть условие неоднородности двухслойной изоляции. Если к двухслойному диэлектрику прикладывать переменное напряжение, то оказывается, что емкость неоднородного диэлектрика зависит от частоты (рис.26). Данная зависимость выражается формулой: C(ω)=Cr+∆C/(1+ω2T2), где ω – круговая частота приложенного напряжения; Т=r∆C – постоянная времени. Подставив выражения для r и ∆С получим: Т=R1R2(C1+C2)/(R1+R2). Форма зависимости С(ω)показана на рис.3. Рис.3. Зависимость емкости двухслойного диэлектрика от частоты. Явление миграционной поляризации широко используется при контроле состояния изоляционных конструкций, в частности их увлажнения и загрязнения. При появлении увлажненного слоя в изоляции ее реакцию на приложение переменного напряжения можно рассматривать в соответствии со схемами замещения рис.2 а, б. Контроль степени увлажнения производится путем измерения емкости изоляции на различных частотах. Из рассмотренного выше механизма миграционной поляризации следует, что емкость изоляции С(ω) с ростом частоты изменяется тем сильнее, чем больше степень неоднородности изоляции, то есть чем больше толщина увлажненного слоя и степень увлажнения. При отсутствии увлажнения (однородной изоляции) емкость от частоты не зависит. 6 На практике для контроля увлажнения изоляции производят измерения емкости при двух частотах: 2 Гц и 50 Гц. Температура при этих измерениях должна находиться в определенных пределах. Чем ближе между собой измеренные значения емкостей С2 и С50, тем качественнее изоляция. На основе опыта установлено, что изоляция недопустимо увлажнена, если измеренные значения различаются более, чем в 1,3 раза, то есть если: С2/С50=1,3. В данной задаче студентам предлагается определить допустимость степени увлажнения по приведенному выше критерию, предполагая, что причиной неоднородности материала заданной изоляционной конструкции является увлажнение. Для контроля увлажнения изоляции путем измерения емкостей на разных частотах существуют специальные приборы контроля влажности (ПКВ). 7 Задача 2. Диэлектрические потери. Условие задачи. Образец диэлектрика прямоугольной формы имеет верхнюю и нижнюю грани с размерами аxb и толщину d. Параметры материала: относительная диэлектрическая проницаемость – εr, удельные объемное и поверхностное сопротивления - соответственно ρ и ρs, тангенс угла диэлектрических потерь при температуре 20°С – tgδ0, коэффициент, характеризующий температурную зависимость тангенса угла диэлектрических потерь α. К верхней и нижней граням прикладывается напряжение величиной U. Исходные данные. Таблица 3. Последняя цифра учебного шифра Параметры a,см b,см d,мм U,В tgδ0.10-3 0 320 220 1.5 700 4.0 1 340 240 1.6 800 3.8 2 360 260 1.7 900 3.6 3 380 280 1.8 1000 3.4 4 400 300 1.9 1100 3.2 5 420 320 2.0 1200 3.0 6 440 340 2.1 1300 2.8 7 460 360 2.2 1400 2.6 8 480 380 2.3 1500 2.4 9 500 400 2.4 1600 2.2 Таблица 4. Предпоследняя цифра учебного шифра Параметры 0 1 2 3 4 5 6 7 8 9 εr 6.0 6.3 6.6 6.9 7.2 7.5 7.8 8.1 8.4 8.7 ρ.1014, 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 ρs.1014,Ом 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 α.10-3,К-1 11 12 13 14 15 16 17 18 19 20 f1, Гц 150 140 130 120 110 100 90 80 60 50 Ом.м Частоты f2 и f3 при всех вариантах вычисляются следующим образом: f2=20f1, f3=20f2. Порядок оформления задачи. 1. Рассчитать объемное и поверхностное сопротивления образца диэлектрика. 2. Рассчитать токи объемной и поверхностной проводимости и сквозной ток через диэлектрик. 3. Рассчитать мощность потерь в образце диэлектрика и удельные диэлектрические потери при приложении постоянного напряжения. 4. Рассчитать емкость образца диэлектрика. 5. Рассчитать мощность потерь в диэлектрике и удельные диэлектрические потери при приложении переменного напряжения с частотами f1, f2 и f3 при температуре 20°С. 6. Рассчитать зависимость тангенса угла диэлектрических потерь от температуры. Расчет произвести в диапазоне температур от 20°С до 120°С с шагом 20°С. Результаты свести в таблицу. 8 7. Рассчитать и изобразить графически зависимости мощности потерь в образце диэлектрика и удельных диэлектрических потерь от температуры при частоте напряжения f1. Расчетные точки взять из пункта 6. Масштабы для построения выбрать самостоятельно. Методические указания к решению задачи. В идеальных диэлектриках свободные электрические заряды отсутствуют, в связи с чем в них протекают только токи, связанные с поляризационными процессами (см. методические указания к задаче 1). При работе диэлектрика на постоянном напряжении эти токи ограничены во времени и протекают только при включении и выключении напряжения. Виды поляризации существуют очень кратковременные (практически мгновенные), а также замедленные, протекающие в течение десятков секунд. При переменном напряжении токи замедленной поляризации (абсорбционные) протекают в течение всего времени нахождения диэлектрика в электрическом поле. В технических диэлектриках всегда присутствует небольшое число свободных зарядов, что приводит к возникновению слабых по величине сквозных стоков. Ток утечки в техническом диэлектрике представляет собой сумму сквозного тока и тока абсорбции: iут=iск+iаб. После окончания процессов поляризации через диэлектрик протекает только сквозной ток iск. Характер зависимости изменения тока утечки через диэлектрик во времени показан на рис.4. Рис.4. Зависимость тока утечки через диэлектрик от времени. Абсорбционные токи необходимо учитывать при измерении проводимости диэлектриков, так как при небольшой выдержке диэлектрика под напряжением эти токи будут регистрироваться наряду со сквозным током. Известно, что у всех используемых в технике диэлектрических материалов поляризация заканчивается в течение 1 минуты, поэтому на практике за сквозной ток принимают ток через диэлектрик через интервал времени после приложения постоянного напряжения, равный 1 мин. Истинное сопротивление диэлектрика Rиз, ток, может быть вычислено следующим образом: определяющее 9 сквозной Rиз=U/(iут-iаб)=U/iск. При переменном напряжении активная проводимость диэлектриков определяется не только сквозным током, но и активными составляющими абсорбционных токов. Процессы электропроводности диэлектриков имеют большое практическое значение в двух аспектах. Во-первых, токи проводимости являются одной из причин рассеяния энергии в диэлектриках (диэлектрических потерь), что вызывает дополнительный нагрев изоляционных конструкций. При определенных условиях диэлектрические потери могут привести к так называемому тепловому пробою диэлектрика. Во-вторых, процессы электропроводности в диэлектриках обычно связаны с присутствием в них небольших количеств различного рода примесей, загрязнений. Эти примеси, как правило, влияют и на электрическую прочность диэлектриков, а следовательно, и на пробивное напряжение всей изоляционной конструкции. Поэтому на практике по току или сопротивлению утечки оценивают состояние изоляции оборудования высокого напряжения перед включением его в работу и при эксплуатации. Кроме того, для оборудования установок постоянного тока процессы электропроводности могут являться основой процессов электрического старения изоляции. Суммарная проводимость твердых электроизоляционных конструкций складывается из объемной и поверхностной проводимостей. Соответствующими характеристиками диэлектрических материалов являются удельная объемная проводимость γ (удельное объемное сопротивление ρ) и удельная поверхностная проводимость γs (удельное поверхностное сопротивление ρs). Как известно, удельные проводимость и сопротивление связаны соотношением γ=1/ρ. Объемная электропроводность - это способность материала диэлектрика проводить ток под действием электрического поля. Удельное объемное сопротивление определяется по формуле: ρ=RS/H, где R – объемное сопротивление образца; S – площадь электрода; H - толщина образца. Поверхностная электропроводность обусловлена присутствием влаги или загрязнений на поверхности диэлектрика. Хотя ток, протекающий вследствие поверхностной электропроводности, протекает не по материалу диэлектрика, а по адсорбированной пленке влаги (загрязнения), сопротивление этой пленки связано с природой диэлектрического материала. Поэтому поверхностную электропроводность рассматривают как свойство самого диэлектрика. Удельное поверхностное сопротивление рассчитывается по формуле: ρs=Rsl/d. где RS - поверхностное сопротивление образца диэлектрика; l - ширина параллельно поставленных электродов; d - расстояние между электродами. Единицы измерения в системе СИ удельного объемного сопротивления – Ом.м, удельного поверхностного сопротивления - Ом. 10 Удельные объемная и поверхностная проводимости будут определяться соответственно: γ=1/ρ γs=1/ρs. Единицы измерения удельной объемной проводимости - См/м, поверхностной - См. Сквозной ток равен сумме токов объемной и поверхностной проводимостей: IСК = IV + IS. Токи объемной и поверхностной проводимостей определяются через объемное и поверхностное сопротивления изоляции. Диэлектрическими потерями называют мощность, рассеиваемую в диэлектрике при воздействии на него электрического поля и вызывающую нагрев диэлектрика. Степень нагрева диэлектрической конструкции определяется удельными диэлектрическими потерями, представляющими собой мощность потерь Р, отнесенную к единице объема. При постоянном напряжении единственной причиной диэлектрических потерь является наличие сквозного тока через диэлектрик, определяемого, как указывалось, объемной и поверхностной проводимостями (сопротивлениями). В этом случае диэлектрические потери при приложении к диэлектрику напряжения U определяются просто: P=Uiск. Удельные диэлектрические потери определяются по следующей формуле: p, Вт/м3, в этом же случае P=E2/ρ=E2γ, где Е – напряженность поля в объеме диэлектрика между электродами, В/м. Для случая простейшего плоского конденсатора с однородным диэлектриком напряженность поля определяется просто: Е=U/d. При переменном напряжении дополнительной причиной диэлектрических потерь служат активные составляющие поляризационных токов. Поэтому при работе диэлектрика на переменном напряжении необходимо использовать другую характеристику материала для расчета диэлектрических потерь. В качестве такой характеристики используется так называемый угол диэлектрических потерь. Рассмотрим это понятие. Диэлектрик без потерь в электрической цепи представляет собой идеальный конденсатор. Как известно, в конденсаторе вектор тока опережает вектор напряжения ровно на 90°, то есть угол сдвига фаз φ=90°. При наличии в диэлектрике потерь этот угол будет меньше 90°, и, чем больше будут потери, тем меньше угол сдвига фаз. 11 Углом диэлектрических потерь δ называется угол, дополняющий до 90° угол фазового сдвига между током и напряжением в диэлектрике: δ=90°-φ. Для идеального диэлектрика без потерь δ=0. С ростом диэлектрических потерь δ увеличивается. Понятие угла диэлектрических потерь иллюстрирует рис.5. Рис.5. Векторная диаграмма диэлектрика с потерями. Вектор тока I можно разложить на две составляющие: активную Iа, совпадающую по направлению с вектором напряжения, и реактивную Iр, опережающую вектор напряжения на 90°. Очевидно, что мощность потерь пропорциональна активной составляющей тока: Р=UIа. Реактивная составляющая вектора тока через диэлектрик есть чисто емкостной ток перезаряда конденсатора. Его можно рассчитать следующим образом: Iр=U/Xc=U/(1/ωC)=UωC, где Хc - емкостное сопротивление; С - емкость диэлектрической конструкции: ω=2f - круговая частота приложенного напряжения. Из геометрических соображений видно (см. рис.5), что: Iа=Iрtgδ=UωCtgδ. Тогда мощность потерь в диэлектрике переменного напряжения будет равна: при приложении к нему P=UIа=U2ωCtgδ, то есть пропорциональна тангенсу угла диэлектрических потерь. В связи с этим, в качестве количественного показателя, характеризующего потери в диэлектрических материалах на переменном напряжении, на практике используется не непосредственно угол диэлектрических потерь δ, а его тангенс tgδ. Эта величина обычно приводится в справочных данных по диэлектрическим материалам. Приведенное выражение показывает, что диэлектрические потери пропорциональны частоте приложенного напряжения (если считать tgδ не зависящим от частоты). 12 Для расчета удельных диэлектрических потерь при приложении к образцу диэлектрика переменного напряжения можно воспользоваться формулой: p=E2ωε0εrtgδ. Емкость диэлектрика для расчета мощности потерь можно определить по формуле: С=ε0εrS/d, где S - площадь граней, к которым подводится напряжение; d - толщина диэлектрика. Следует отметить, что для диэлектриков с большими потерями емкость становится совершенно условной величиной и расчет потерь значительно усложняется. Однако на практике такие случаи встречаются достаточно редко. Тангенс угла диэлектрических потерь в условиях эксплуатации величина не постоянная. Основным фактором, влияющим на tgδ твердых диэлектриков, является температура. Для различных диэлектрических материалов зависимость тангенса угла диэлектрических потерь от температуры различна. В то же время для большинства материалов, имеющих широкое распространение в технике, эта зависимость может быть хорошо описана экспоненциальным законом: tgδ = tgδ0 .exp[α(T–Т0)], где tgδ0 – тангенс угла диэлектрических потерь при температуре Т0; tgδ – тангенс угла диэлектрических потерь при температуре Т; α - постоянный коэффициент, характеризующий материал. Этим законом следует пользоваться при решении данной задачи расчетно-графической работы. 13 Задача 3. Магнитомягкие материалы. Условие задачи. Сердечник из электротехнической стали прямоугольной формы с площадью сечения S и длиной l работает в переменном магнитном поле с частотой 50 Гц и амплитудой Вm. Для материала сердечника известны кривая намагничивания В=f(Н) и зависимость удельных потерь от амплитуды магнитной индукции рB/f=φ(Вm) для данной частоты. Исходные данные. Кривая намагничивания материала выбирается из табл.5 по последней цифре учебного шифра студента. Зависимость удельных потерь рB/f=φ(Вm) общая для всех вариантов и приведена в табл.6. Размеры сердечника выбираются по последней цифре шифра, амплитуда магнитной индукции - по предпоследней: эти данные приведены в табл.7. Плотность магнитного материала принимается одинаковой для всех вариантов и равной 7,65.103 кг/м3. Таблица 5. Кривые намагничивания материала сердечника. Последняя цифра учебного шифра 0 1 2 3 4 5 6 7 8 9 Значения параметров: Н, кА/м; В, Тл Н В Н В Н В Н В Н В Н В Н В Н В Н В Н В 0.1.10-3 5.4.10-5 0.1.10-3 5.2.10-5 0.1.10-3 5.1.10-5 0.1.10-3 4.9.10-5 0.1.10-3 5.5.10-5 0.1.10-3 5.3.10-5 0.1.10-3 4.8.10-5 0.1.10-3 5.3.10-5 0.1.10-3 4.9.10-5 0.1.10-3 5.0.10-5 0.25 1.10 0.25 1.00 0.25 0.96 0.25 0.98 0.25 1.20 0.25 1.05 0.25 1.15 0.25 1.17 0.25 1.03 0.25 1.17 1.00 1.45 1.00 1.35 1.00 1.25 1.00 1.30 1.00 1.55 1.0 1.40 1.00 1.50 1.00 1.51 1.00 1.43 1.00 1.52 2.50 1.70 2.50 1.60 2.00 1.45 2.00 1.45 2.50 1.80 2.50 1.65 2.00 1.70 2.50 1.73 2.00 1.78 2.50 1.76 5.00 1.88 5.00 1.79 4.00 1.75 4.00 1.77 5.00 1.98 5.00 1.84 5.00 1.93 5.00 1.89 4.00 1.84 5.00 1.95 10.00 1.94 10.00 1.86 10.00 1.85 10.00 1.87 10.00 2.04 10.00 1.91 10.00 1.99 10.00 1.95 8.00 1.97 10.00 2.01 15.00 1.95 15.00 1.87 16.00 1.86 16.00 1.88 16.00 2.05 15.00 1.92 15.00 2.00 16.00 1.96 16.00 1.98 15.00 2.02 14 Таблица 6. Зависимость удельных потерь в магнитном материале от амплитуды магнитной индукции при частоте 50 Гц. Bm, Тл PB/50,Вт/кг 0.5 0.3 1.0 1.1 1.5 2.5 1.7 3.2 2.0 4.4 Таблица 7. Размеры сердечника и амплитуда магнитной индукции по вариантам. Параметры Последняя цифра шифра 0 1 2 S, см2 l, м 40 0.30 45 0.29 50 0.28 Bm, Тл 0 0.9 1 1.0 2 1.1 3 4 5 6 7 55 60 65 70 75 0.27 0.26 0.25 0.24 0.23 Предпоследняя цифра шифра 3 1.2 4 1.3 5 1.4 6 1.5 7 1.6 8 9 80 0.22 85 0.21 8 1.7 9 1.8 Порядок оформления задачи. 1. Изобразить графически заданную кривую намагничивания материала сердечника. 2. Рассчитать и изобразить графически зависимость магнитной проницаемости материала от напряженности магнитного поля. Расчетные значения напряженности поля взять из исходной таблицы кривой намагничивания. 3. Определить начальную и максимальную магнитные проницаемости и индукцию насыщения материала сердечника. 4. Построить график зависимости удельных потерь в материале от амплитуды магнитной индукции. 5. Определить удельные магнитные потери при заданной в задании величине магнитной индукции. 6. Рассчитать потери мощности в сердечнике. Методические указания к решению задачи. По магнитным свойствам материалы подразделяются на слабомагнитные и сильномагнитные. Сильномагнитные материалы (в технике для сокращения их называют просто магнитными) имеют большое значение магнитной проницаемости (μr>1), в связи с чем они нашли широкое распространение в конструкциях электрических машин и аппаратов. Как известно, величина магнитной проницаемости характеризует способность материала усиливать магнитное поле. К магнитным материалам относятся ферромагнетики и ферримагнетики. Наиболее широко распространенные ферромагнитные материалы - железо, никель, кобальт и их сплавы. 15 Магнитные свойства материалов обусловлены внутренними скрытыми формами движения электрических зарядов, представляющими собой элементарные круговые токи. Для ферромагнитных материалов характерным является наличие самопроизвольной (спонтанной) намагниченности вещества в пределах некоторых макроскопических областей, называемых магнитными доменами. Однако направления магнитных моментов отдельных доменов в отсутствие внешнего поля будут самыми различными, и магнитный поток такого тела во внешнем пространстве будет равен нулю. При помещении ферромагнитного материала во внешнее магнитное поле магнитные домены будут ориентироваться по его направлению, магнитное поле доменов будет складываться с внешним магнитным полем, вследствие чего возникает эффект усиления магнитного поля. Протекание процессов намагничивания ферромагнитного материала характеризуется кривой намагничивания - зависимостью магнитной индукции от напряженности магнитного поля В=f(H). Для всех ферромагнетиков эти кривые имеют сходный характер. Общая формула зависимости магнитной индукции от напряженности магнитного поля следующая: B=μ0μrH, где μ0=4.l0-7 Гн/м - магнитная постоянная; μ - относительная магнитная проницаемость материала. Относительную магнитную проницаемость в технике сокращенно называют просто магнитной проницаемостью. По определению она есть отношение индукции к напряженности магнитного поля с учетом магнитной постоянной: μr=В/(μ0H). Численно магнитная проницаемость показывает, во сколько раз магнитная индукция в веществе будет больше индукции в вакууме при той же напряженности магнитного поля. Известно, что у вакуума μr=1, У слабомагнитных (немагнитных) материалов μr≈1 (у диамагнетиков μr<1, у парамагнетиков μr>1). Особенностью ферромагнитных материалов кроме большого значения магнитной проницаемости (μr>>1) является ее зависимость от напряженности магнитного поля. Вследствие этого кривая намагничивания ферромагнитных материалов имеет нелинейную форму, вид которой представлен на рис. 6. Из этого рисунка видно, что магнитная индукция в ферромагнетике возрастает не беспредельно, а до некоторого значения, называемого индукцией насыщения Bmax. Индукция насыщения достигается при условии переориентации всех доменов по направлению внешнего поля. 16 Рис. 6. Кривая намагничивания ферромагнитного материала. В связи с этим обстоятельством на практике свойства магнитных материалов характеризуются несколькими значениями магнитной проницаемости: начальной магнитной проницаемостью μrн - значением μr при Н=0 и определяемой в очень слабых полях (порядка 0,1 А/м); максимальной магнитной проницаемостью μrmax - наибольшим ее значением; динамической магнитной проницаемостью - отношением наибольшего значения индукции к наибольшему значению напряженности магнитного поля (с учетом магнитной постоянной) при работе материала в переменном магнитном поле. По кривой намагничивания материала можно определить характер зависимости магнитной проницаемости ферромагнитных материалов от напряженности магнитного поля. Очевидно, что магнитная проницаемость пропорциональна крутизне кривой намагничивания. Как видно из рис.6, в слабых полях (при малых Н) кривая намагничивания пологая, и магнитная проницаемость мала. Далее крутизна кривой намагничивания и, соответственно, магнитная проницаемость увеличиваются. При определенном значении напряженности магнитного поля магнитная проницаемость достигает максимального значения. Затем крутизна кривой намагничивания уменьшается, и магнитная проницаемость падает. При достижении области насыщения магнитная проницаемость становится равной практически единице. Характер изменения магнитной проницаемости в процессе намагничивания ферромагнитного материала показан на рис.7. Рис.7. Зависимость магнитной проницаемости от напряженности магнитного поля. 17 На рис.6 показана основная кривая намагничивания - характер изменения магнитной индукции от напряженности магнитного поля при намагничивании ферромагнетика от полностью размагниченного состояния. При уменьшении напряженности поля от какого-либо значения индукция также будет уменьшаться, но не по основной кривой, а с отставанием, что называют явлением гистерезиса. При снижении напряженности поля до нуля индукция до нуля не уменьшится. Для того чтобы размагнитить материал потребуется определенная напряженность магнитного поля противоположного направления. Таким образом, образуется гистерезисный цикл перемагничивания (петля гистерезиса). В зависимости от степени намагничивания материала получаются различные петли гистерезиса. Пример семейства петель гистерезиса показан на рис.8. Р и с.8. Циклы перемагничивания ферромагнитного материала. Из всех возможных циклов перемагничивания наибольший интерес с практической точки зрения представляет предельный цикл, при котором достигается намагничивание материала до насыщения, то есть до индукции Вmax. По петле предельного цикла определяются два важных параметра ферромагнитных материалов: остаточная индукция Вr - индукция при уменьшении напряженности магнитного поля до нуля в процессе размагничивания материала, намагниченного до насыщения; коэрцитивная сила Нс - обратно направленная по отношению к намагничивающему направлению напряженность магнитного поля, необходимая для размагничивания материала (снижения индукции до нуля). По значение коэрцитивной силы все магнитные материалы делятся на две группы: 1) магнитомягкие - материалы с малым значением коэрцитивной силы и больной магнитной проницаемостью; 2) магнитотвердые - материалы с большой коэрцитивной силой и сравнительно малой магнитной проницаемостью, имеющие большую остаточную индукцию. 18 Магнитомягкие материалы применяются для сердечников электрических машин и аппаратов, в измерительных приборах, там где при наименьших затратах энергии требуется достичь наибольшей индукции, а магнитотвердые - в качестве материала постоянных магнитов. При перемагничивании ферромагнетиков в переменных магнитных полях всегда имеются тепловые потери, они обусловлены потерями на гистерезис и динамическими потерями. Динамические потери вызываются вихревыми токами, индуцированными в массе магнитного материала, а отчасти так называемым магнитным последействием (магнитной вязкостью}. Потери на гистерезис для каждого материала могут быть определены по площади статической петли гистерезиса с учетом масштабов по осям и частоты тока. Их аналитический расчет затруднен из-за сложной формы петли гистерезиса. Поэтому для вычисления потерь на гистерезис используют эмпирические формулы. Потери энергии за один цикл перемагничивания в единице объема вещества рассчитывается по формуле: Wн1=ηBnmax, где η - коэффициент, зависящий от материала; Вmax - максимальная индукция, достигаемая в течение цикла; n - показатель степени, равный 1,6 … 2,0. Тогда мощность, расходуемая на гистерезис, будет равна: Pн=ηBnmaxfV, где f - частота тока; V - объем ферромагнитного материала. Потери на вихревые токи зависят от электрического сопротивления ферромагнитного сердечника. Чем выше удельное сопротивление ферромагнетика, тем меньше потери на вихревые токи. Для мощности, расходуемой на вихревые токи, также используется эмпирическая формула: Pf=ζB2maxf2V, где ζ - коэффициент, зависящий от материала сердечника (в частности от его удельного сопротивления) и его формы. Поскольку Рf пропорциональна второй степени частоты, а Рн - первой степени, при высоких частотах доминирующими являются потери на вихревые токи. Это ограничивает применение на высоких частотах ферромагнитных материалов с высокими магнитными характеристиками, но с малым удельным электрическим сопротивлением (электротехнических сталей, пермаллоев и т.п.). Для уменьшения потерь на вихревые токи в магнитных сердечниках используют магнитомягкие материалы с повышенным удельным электрическим сопротивлением, а также выполняют их в виде собранных из отдельных изолированных друг от друга листов. Потери, связанные с магнитным последействием, учитываются в специальных случаях при использовании ферромагнитных материалов в импульсных режимах. 19 В инженерной практике для упрощения расчета потерь в ферромагнетиках при работе в переменных магнитных полях для магнитомягких материалов в справочных данных обычно задаются удельные потери - мощность потерь, приходящаяся на единицу массы материала: PB/f=P/m. где Р - суммарные потери в образце материала; m - масса образца материала. Как показывают приведенные выше формулы, мощность потерь в ферромагнетиках зависит от амплитуды магнитной индукции и частоты. Поэтому в справочных данных обычно приводится несколько значений удельных потерь для определенных значений величин магнитной индукции и частота. В буквенном обозначении удельных потерь нижний индекс показывает значения магнитной индукции и частоты. При известных удельных потерях мощность потерь в ферромагнитном сердечнике вычисляется достаточно просто: Р=PB/fVλ, где λ- плотность материала. 20 Задача 4. Магнитотвердые материалы. Условие задачи. Для магнитотвердого В=f(H). материала задана кривая размагничивания Исходные данные. Таблица 8. Кривые размагничивания магнитотвердых материалов. Последняя цифра шифра 0 1 2 3 4 5 6 7 8 9 Значения параметров: В, Тл и Н, кА/м H 0 10 20 30 40 50 53 B 1.33 1.32 1.3 1.27 1.22 0.90 0 H 0 10 20 30 40 50 62 B 1.28 1.27 1.25 1.22 1.18 1.02 0 H 0 10 20 25 30 40 45 B 1.23 1.21 1.16 1.10 1.04 0.80 0 H 0 10 20 25 30 40 51 B 1.20 1.15 1.09 1.05 1.00 0.85 0 H 0 10 20 30 40 50 59 B 1.10 1.06 0.99 0.88 0.74 0.42 0 H 0 10 20 30 40 50 56 B 0.89 0.84 0.76 0.64 0.47 0.18 0 H 0 20 40 60 70 80 87 B 0.80 0.72 0.63 0.49 0.37 0.18 0 H 0 10 20 25 30 40 48 B 0.75 0.66 0.55 0.48 0.40 0.22 0 H 0 10 20 25 30 40 45 B 0.60 0.55 0.47 0.41 0.34 0.15 0 H 0 10 20 30 40 50 53 B 0.50 0.45 0.39 0.30 0.22 0.05 0 21 Порядок оформления задачи. 1. Построить кривую размагничивания заданного магнитотвердого материала по исходным данным. На графике предусмотреть место для последующего построения кривой удельной магнитной энергии. 2. Определить остаточную индукцию и коэрцитивную силу материала. 3. Рассчитать и изобразить графически зависимость удельной магнитной энергии в воздушном зазоре от магнитной индукции. Построение оформить вместе с кривой размагничивания. 4. Определить максимальное значение удельной магнитной энергии и соответствующие ему значения магнитной индукции материала и напряженности магнитного поля. 5. Рассчитать коэффициент выпуклости кривой размагничивания материала. Методические указания к решению задачи. Магнитотвердыми называют магнитные материалы с большой коэрцитивной силой. Такие материалы обладают значительной остаточной индукцией и сравнительно малой магнитной проницаемостью. Основное применение магнитотвердые материалы нашли для изготовления постоянных магнитов. В связи о другой областью применения свойства магнитотвердых материалов характеризуются показателями, отличающимися от используемых для магнитомягких материалов. Основными количественными характеристиками магнитотвердых материалов служат коэрцитивная сила, остаточная индукция и максимальная удельная энергия, отдаваемая магнитом во внешнее пространство. Магнитная проницаемость магнитотвердых материалов меньше, чем магнитомягких, причем чем больше коэрцитивная сила, тем меньше магнитная проницаемость. Кроме того, в связи со специфической областью применения для описания свойств магнитотвердых материалов используются специфические зависимости, а именно: кривая размагничивания зависимость В=f(Н) при размагничивании материала от индукции насыщения (II квадрант предельной петли гистерезиса) и зависимость удельной магнитной энергии в воздушном зазоре магнита от магнитной индукции. Обычно эти зависимости строятся вместе, их примерный вид показан на рис.9. Рис. 9. Кривые размагничивания (1) и удельной магнитной энергии в воздушном зазоре (2). 22 Рассмотрим форму кривой магнитной энергии. При замкнутом состоянии магнита (в виде кольцевого сердечника) магнитный поток, а следовательно, и магнитная энергия находятся внутри него. Во внешнее пространство энергия будет отдаваться в том случае, если между полюсами магнита будет воздушный зазор. Причем величина отдаваемой энергии зависит от величины воздушного зазора. Удельная магнитная энергия (энергия, приходящаяся на единицу объема материала магнита), заключенная в воздушном зазоре, определяется по формуле: Wd=(BdHd)/2, где Нd - напряженность поля, соответствующая индукции Вd (см. рис. 8). При замкнутом магните Вd=Br, Нd=0, вследствие чего отдаваемая энергия равна нулю. При очень большом зазоре между полюсами будет Нd=Нc, но Вd=0, и энергия также стремится к нулю. Энергия в воздушное пространство будет отдаваться магнитом при наличии воздушного зазора не предельно большого по величине, когда Вd≠0 и Нd≠0. При определенной величине зазора между полюсами энергия достигает максимального значения: Wmax=(Bd’Hd’)/2=(ВН)max/2, где Вd’ и Нd’ - магнитная индукция и напряженность магнитного поля, соответствующие данному воздушному зазору (см. рис.8). Wmax - наиболее важная характеристика магнитотвердых материалов для постоянных магнитов. Так как Wmax - максимальное значение удельной, приходящейся на единицу объема, энергии, отдаваемой в воздушное пространство магнитом, то единицей измерения этой величины в системе СИ будет Дж/м3 (на практике чаще - кДж/м3). В технике часто для характеристики магнитотвердых материалов пользуются не величиной Wmax, а произведением Вd’Нd’, опуская множитель 1/2, а также используют коэффициент выпуклости кривой размагничивания материала: β=(ВН)max/(ВrНc)=Bd’Hd’/(BrHc). Чем более выпуклую форму имеет кривая размагничивания при определенных значениях индукции насыщения и коэрцитивной силы, тем больше энергия, отдаваемая магнитом во внешнее пространство. При более выпуклой форме коэффициент выпуклости кривой размагничивания больше. 23 Литература. 1. Богородицкий Н.П., Пасынков В.В., Т а р е е в Б.М. Электротехнические материалы: Учебник для вузов. – 7-е изд., перераб. и доп. - Л.: Энергоатомиздат. Ленингр. отд-ние, 1985. – 304 с., ил. 2.Пасынков В. В., Сорокин В. С. Материалы электронной техники: Учеб. для студ. вузов по спец. «Полупроводники и диэлектрики», «Полупроводниковые и микроэлектронные приборы». – 2-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 367 с., ил. 3.Справочник по электротехническим материалам. В 3 т. / Под ред. Ю. В. Корицкого и др. – М.: Энергоатомиздат. – 1986. 4.Электротехнические и конструкционные материалы: Учеб. пособие для студ. учреждений сред. проф. образования. / В. Н. Бородулин, А. С. Воробьев, В. М. Матюнин и др.; Под ред. В. А. Филикова. – М.: Мастерство: Высшая школа, 2000. – 280 с.