Вычислительная теплопередача и гидродинамика

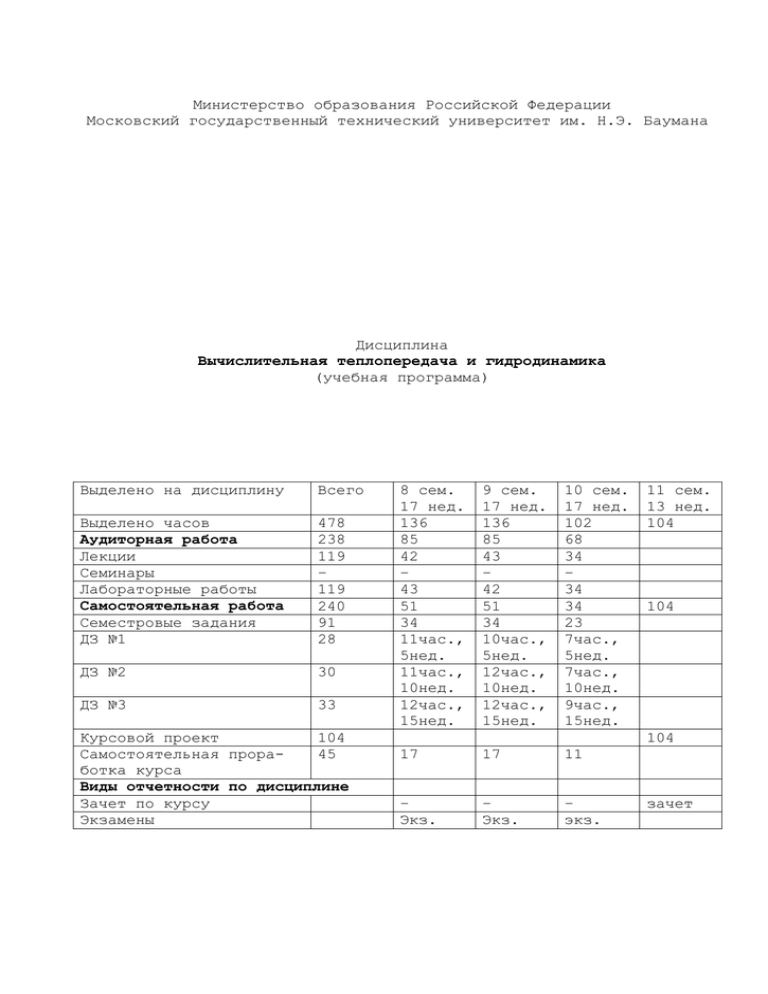
Министерство образования Российской Федерации
Московский государственный технический университет им. Н.Э. Баумана
Дисциплина
Вычислительная теплопередача и гидродинамика
(учебная программа)
Выделено на дисциплину
Всего
Выделено часов
Аудиторная работа
Лекции
Семинары
Лабораторные работы
Самостоятельная работа
Семестровые задания
ДЗ №1
478
238
119
–
119
240
91
28
ДЗ №2
30
ДЗ №3
33
Курсовой проект
104
Самостоятельная прора45
ботка курса
Виды отчетности по дисциплине
Зачет по курсу
Экзамены
8 сем.
17 нед.
136
85
42
–
43
51
34
11час.,
5нед.
11час.,
10нед.
12час.,
15нед.
9 сем.
17 нед.
136
85
43
–
42
51
34
10час.,
5нед.
12час.,
10нед.
12час.,
15нед.
10 сем.
17 нед.
102
68
34
–
34
34
23
7час.,
5нед.
7час.,
10нед.
9час.,
15нед.
17
17
11
–
Экз.
–
Экз.
–
экз.
11 сем.
13 нед.
104
104
104
зачет
1. Цели и задачи дисциплины
Мы являемся свидетелями резкого роста роли и значения нового
подхода к решению задач теплообмена и динамики жидкости, который
получил название вычислительной теплопередачи и гидродинамики.
Несмотря на то, что эксперимент по-прежнему играет очень важную роль, отчетливо проявляется тенденция к все более широкому использованию вычислительного подхода. Эта тенденция во многом связана с тем, что в последние годы рост быстродействия компьютеров
опережал рост их стоимости, вследствие чего стоимость расчетов
фантастически уменьшилась и продолжает уменьшаться (на порядок
каждые 8 лет).
Курс «Вычислительная теплопередача и гидродинамика» знакомит
студентов с необходимыми разделами высшей математики и сущностью
численных методов (8-й семестр). В течение 9-го семестра студенты
учатся работать с программным комплексом (ПК) ДСПТ (Двухмерные
Стационарные Параболические Течения), предназначенным для численного решения (методом конечных разностей) систем дифференциальных
уравнений с частными производными параболического типа (уравнений
пограничного слоя). Во время 10-го семестра изучается ПК ANSYS
(основанный на методе конечных элементов), с помощью которого можно решать практически любые инженерные и исследовательские задачи.
При выполнении курсового проекта (11-й семестр) студенты имеют
возможность применить все свои знания в области вычислительной
теплопередачи и гидродинамики.
Основная цель дисциплины - подготовка специалиста к расчетным
исследованиям в области тепломассообмена и гидродинамики с помощью
численных методов.
В результате изучения данной дисциплины студенты должны
знать:
- способы выражения законов сохранения количества движения,
теплоты, массы и т.п. в форме математических моделей соответствующих явлений;
- способы нахождения соотношений, выражающих зависимость интенсивности тепломассообмена от различных факторов;
- методику применения расчетных соотношений и справочных материалов для анализа процессов тепломассообмена;
- методику проведения вычислительного эксперимента для изучения основных видов теплопередачи;
- методику воплощения математической модели изучаемого явления в компьютерную программу.
Студенты должны уметь:
- обоснованно выбирать математическую модель для описания
изучаемого или рассчитываемого процесса;
- правильно использовать теоретические и эмпирические соотношения для расчета процессов тепломассообмена и динамики жидкости;
- выполнять расчеты, анализировать и обобщать результаты расчетов,
- пользоваться справочными материалами в виде рекомендуемых
формул, таблиц, диаграмм и т.п.;
- применять алгоритмические языки высокого уровня для математического моделирования процессов тепломассообмена и динамики жидкости.
Материал дисциплины опирается на знания студентов, предварительно полученные при изучении курсов математики, физики, алгоритмических языков и программирования, термодинамики, теории тепломассообмена, газовой динамики, курса «Введение в численные методы».
Лабораторные работы проводятся за экранами компьютеров.
2. Содержание дисциплины
8 семестр
2.1. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
42 часа
2.1.1. Основные понятия и определения - 6 часов.
Модельные уравнения конвекции, диффузии с конвекцией и различные законы сохранения для сплошных сред. Классификация уравнений в частных производных. Сетка и сеточные функции. Определение и
примеры сходимости. Определение и примеры аппроксимации. Определение и примеры устойчивости. Согласованность разностной схемы.
2.1.2. Простейшие приемы построения аппроксимирующих разностных схем – 5 часов.
Замена производных разностными соотношениями. Схемы первого
порядка точности. Свойство монотонности. Диссипативное свойство.
Схемы второго порядка точности и их немонотонность. Интегроинтерполяционный метод. Метод неопределенных коэффициентов. Схемы
типа предиктор–корректор. Примеры конструирования граничных условий при построении разностных схем.
2.1.3. Основные приемы исследования устойчивости разностных
схем – 6 часов.
Условие Куранта–Фридрихса–Леви, необходимое для сходимости.
Примеры разностных схем для задачи Коши и Дирихле. Устойчивость по
начальным данным. Необходимое спектральное условие устойчивости.
Сходимость как следствие аппроксимации и устойчивости (зависимость
между аппроксимацией, устойчивостью и сходимостью). Выглаживание
разностного решения как действие аппроксимационной вязкости. Принцип замороженных коэффициентов. Принцип максимума для явной и неявной разностных схем на примере уравнения теплопроводности. Метод
прогонки. Устойчивость метода прогонки. Понятие о матричной и потоковой прогонке.
2.1.4. Понятие о разностных схемах для расчета обобщенных решений – 3 часа.
Механизм возникновения разрывов. Определение обобщенного решения. Условия на линии разрыва решения. Распад произвольного разрыва. Схемы для нахождения обобщенных решений: с искусственной
вязкостью, метод характеристик. Дивергентные разностные схемы.
2.1.5. Понятия о разностных схемах расщепления – 4 часа.
Конструирование схем расщепления. Экономичные разностные схемы. Расщепление по физическим факторам. Применение метода расщепления для построения экономичных разностных схем на примере одномерных уравнений газовой динамики.
2.1.6. Эллиптические задачи – 8 часов.
Простейшая разностная схема для задачи Дирихле: аппроксимация
и устойчивость. Идея метода установления. Анализ явной схемы установления. Схема переменных направлений. Метод релаксации решения
системы пятиточечных конечно-разностных уравнений (метод Зейделя,
верхняя и нижняя релаксации, прогонка по линиям). Итерационные методы с переменным шагом. Чебышевский набор параметров. Метод Дугласа–Рэкфорда.
2.1.7. Понятие о вариационно-разностных и проекционно-разностных схемах – 10 часов.
Вариационная постановка краевых задач. Вариационный метод
Ритца. Проекционный метод Галеркина. Способы решения алгебраической системы. Понятие о многосеточном методе Федоренко. Вычислительная устойчивость. Пример вариационно-разностной схемы для первой краевой задачи. Сопоставление вариационно-разностных схем с
обычными разностными схемами.
Лабораторные работы – 43 часа
1. Решение граничных задач: сведением их к задачам
Коши; методом вариации постоянных; методом пристрелки; методом дифференциальной прогонки . . . .
2. Решение граничных задач методом Галеркина
и методом моментов . . . . . . . . . . . . . . . .
3. Решение граничных задач интегро-интерполяционным методом и методом сеток . . . . . . . . .
4. Метод прогонки . . . . . . . . . . . . . . . . .
5. Методики построения разностных схем . . . . . . .
6. Погрешность аппроксимации дифференциальной
задачи разностной схемой . . . . . . . . . . . .
7. Сходимость и устойчивость разностных схем . . . .
8. Решение смешанной задачи для уравнения
теплопроводности методом сеток . . . . . . . . .
9. Решение смешанной задачи для уравнений
гиперболического типа методом сеток . . . . . . .
10. Решение задачи Дирихле для уравнения
Пуассона методом сеток
. . . . . . . . . . . .
11. Использование компьютера при решении прямыми
методами систем линейных алгебраических уравнений специального типа: метод матричной прогонки; специальный метод матричной прогонки;
метод полной редукции . . . . . . . . . . . . . .
12. Метод Галеркина для многомерных уравнений . . . .
13. Вариационный принцип . . . . . . . . . . . . . .
14. Исследование итерационных методов . . . . . . . .
4 часа.
3 часа.
3 часа.
4 часа.
3 часа.
2 часа.
3 часа.
3 часа.
3 часа.
3 часа.
4
2
4
2
часа.
часа.
часа.
часа.
Самостоятельная работа – 51 час
Домашние задания
34 часа
1. Решение смешанной задачи для уравнения
теплопроводности методом сеток . . . . . . . . . 11 часов.
2. Решение задачи Дирихле для уравнения
Пуассона методом сеток . . . . . . . . . . . . . 11 часов.
3.
– 12 часов.
Самостоятельная проработка курса – 17 часов.
Работа с учебниками. Проработка разделов курса, отнесенных
для самостоятельного изучения. Подготовка к лабораторным занятиям.
9 семестр
2.2. ПРОГРАМНЫЙ КОМПЛЕКС ДСПТ (Двухмерные Стационарные Параболические Течения)
43 часа
2.2.1. Введение- 2 часа.
Преимущества
компьютерного
математического
моделирования.
Цель курса. Содержание курса. Основные понятия и определения. Примеры течений типа двухмерного пограничного слоя.
2.2.2. Математические модели параболических течений (течений
типа двухмерного пограничного слоя) – 4 часа.
Односторонние и двухсторонние координаты. Системы координат.
Уравнения пограничного слоя. Законы переноса. Общая форма уравнений пограничного слоя. Преобразование уравнения энергии к нестационарному одномерному дифференциальному уравнению теплопроводности.
2.2.3. Вывод конечно-разностных уравнений, аппроксимирующих
дифференциальные уравнения пограничного слоя – 9 часов.
Контрольные объемы. Изменение зависимой переменной в контрольном объеме. Точное решение конвективно-диффузионного дифференциального уравнения без источников. Выбор конечно-разностной
схемы. Полное конечно-разностное уравнение. Решение системы конечно-разностных уравнений методом прогонки. Определение количества
жидкости, вовлекаемой в расчетную область на каждом шаге по продольной координате. Вычисление неизвестного градиента давления в
случае течения в канале.
2.2.4. Введение в компьютерную программу – 6 часов.
Процедура решения. Величины, определяющие узловые точки, поверхности раздела контрольных объемов. Логические переменные.
Идентификаторы основных переменных. Структурная схема программы.
Краткое описание подпрограмм основного блока программного комплекса. Блок программ пользователя USER. Подготовка к решению задачи.
2.2.5. Одномерная нестационарная теплопроводность двухслойной
пластины с источником тепла – 3 часа.
2.2.6. Ламинарный пограничный слой на плоской пластине – 3
часа.
2.2.7. Осесимметричная турбулентная струя – 4 часа.
2.2.8. Ламинарный пограничный слой: пленочное охлаждение,
пристенный тангенциальный вдув, сжимаемость, переменная вязкость,
кинетический нагрев, градиент давления – 4 часа.
2.2.10. Течение в осесимметричном канале (пористое охлаждение) – 2 часа.
2.2.11. Пограничный слой в сопле Лаваля. Модель турбулентности k- - 6 часов.
Лабораторные работы – 42 часа
1. Расчет толщины вытеснения и толщины потери
импульса (численное интегрирование методом
трапеций и по правилу Симпсона) . . . . . . .
2. Решение нелинейных алгебраических уравнений
методом Ньютона-Рафсона . . . . . . . . . . .
3. Аппроксимация экспериментальных данных методом
наименьших квадратов . . . . . . . . . . . . .
4. Одномерная задача нестационарной теплопроводности . . . . . . . . . . . . . . . . . . . .
5. Ламинарный гидродинамический и температурный
пограничные слои на плоской пластине (безградиентное течение) . . . . . . . . . . . . . .
6. Ламинарная естественная конвекция на вертикальной изотермической плоской стенке . . . .
7. Отсасывание пограничного слоя как способ
предотвращения его отрыва от обтекаемой
поверхности . . . . . . . . . . . . . . . . .
8. Полностью развитое течение в круглой трубе
(проверка формулы Хагена-Пуазейля) . . . . . .
9. Ламинарная радиальная пристенная струя . . . .
. 4 часа.
. 4 часа.
. 5 часов.
. 5 часов.
. 5 часов
. 5 часов.
. 4 часа.
. 5 часов.
. 5 часов
Самостоятельная работа – 51 час
Домашние задания
34 часа
1. Дифференциальные уравнения пограничного
слоя, системы координат и конечно-разностная схема . . . . . . . . . . . . . . . . .
2. Нестационарная теплопроводность цилиндрической стенки и ребра постоянного попереч-
10 часов.
ного сечения . . . . . . . . . . . . . . . . . . 12 часов.
3. Температурный пограничный слой при ламинарном течении в трубе круглого поперечного
сечения . . . . . . . . . . . . . . . . . . . . 12 часов.
Самостоятельная проработка курса – 17 часов.
Работа с учебниками. Проработка разделов курса, отнесенных
для самостоятельного изучения. Подготовка к лабораторным занятиям.
10 семестр
2.3. ПРОГРАМНЫЙ КОМПЛЕКС ANSYS
34 часа
2.3.1. Введение – 2 часа.
Метод конечных элементов (МКЭ). ANSYS – наиболее отработанный, оттестированный и удобный пакет программ для применения в инженерной практике.
2.3.2. Общие сведения о программе ANSYS и необходимые предварительные замечания – 2 часа.
2.3.3. Инструментарий ANSYSа – 10 часов.
Меню файл (File), меню выбор (Select), меню список (List),
меню
график
(Plot),
меню
управления
графическим
выводом
(PlotCtrls), меню рабочая плоскость (Work Plane), меню параметры
(Parameter),
меню
макро
(Macro),
управление
меню
утилит
(MenuCtrls), меню помощь (Help).
2.3.4. Линейка инструментов (Toolbar) – 2 часа.
2.3.5. Препроцессор – 8 часов.
Выбор типа конечного элемента. Задание свойств материала
(среды), задание свойств жидкостей при решении задач гидрогазодинамики. Построение геометрической модели. Создание конечно-элементной модели. Задание граничных и начальных условий.
2.3.6. Решение задачи – 4 часа.
Подготовка к решению. Методы решения систем алгебраических
уравнений с разреженной матрицей. Решение и прерывание решения.
Рестарт.
2.3.7. Постпроцессор – 6 часов.
Чтение результатов. Графическое отображение результатов.
Отображение изолиний и векторов. Отображение траекторий частиц.
Отображение по запросу. Построение графиков вдоль заданного пути.
Табличное представление результатов расчета. Постпроцессор POST26.
Лабораторные работы – 34 часа
1. Введение в ANSYS . . . . . . . . . . . . . . . .
4 часа.
2.
3.
4.
4.
Меню утилит . . . . . . . . . . . .
Меню утилит . . . . . . . . . . . .
Построение геометрической модели . .
Теплофизические свойства, начальные
и граничные условия . . . . . . . .
5. Нестационарная и стационарная теплопроводность . . . . . . . . . . . .
7. Конвективный теплообмен . . . . . .
8. Радиационный теплообмен . . . . . .
Домашние задания
. . . . . .
. . . . . .
. . . . . .
4 часа.
4 часа.
6 часов.
. . . . . .
4 часа.
. . . . . .
. . . . . .
. . . . . .
4 часа.
4 часа.
4 часа.
23 часа
1. Нестационарная и стационарная теплопроводность . . . . . . . . . . . . . . . . . .
2. Конвективный теплообмен . . . . . . . . . . . .
3. Радиационный теплообмен . . . . . . . . . . . .
7 часов.
7 часов.
9 часов.
Самостоятельная проработка курса – 11 часов.
Работа с учебниками. Проработка разделов курса, отнесенных
для самостоятельного изучения. Подготовка к лабораторным занятиям.
11 семестр
Курсовой проект – 104 часа.
Целью курсового проекта является проектирование элементов
конструкций промышленных и научно-исследовательских установок.
Непосредственное проектирование предваряет численный расчет гидродинамики и тепломассообмена в этих элементах конструкций.
Объем графической части курсового проекта составляет 2-3 листа, объем расчетно-пояснительной записки к курсовому проекту составляет 30-35 листов.
3. Учебно-методические материалы
8 семестр
Основная литература
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие. – М.: Гл. ред. физ. – мат. лит., 1987. –600 с.
2. Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие
для вузов. - М.: Гл. ред. физ. – мат. лит., 1989. –482 с.
3. Рябенький В.С. Введение в вычислительную математику: Учеб.
пособие для вузов. - М.: ФИЗМАТЛИТ, 2000. –294 с.
Дополнительная литература
1. Ковеня В.М., Яненко Н.Н. Метод расщепления в задачах газовой динамики. Новосибирск: Наука, 1981. – 303 с.
2. Ши Д. Численные методы в задачах теплообмена. – М.:Мир,
1988. – 544 с.
3. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы
в задачах и упражнениях. – М.: Высшая школа, 2000. – 188 с.
9 семестр
Основная литература
1. Патанкар С., Сполдинг Д. Тепло- и массообмен в пограничных
слоях: Пер. с англ. – М.: «Энергия», 1971. – 127 с.
2. Шлихтинг Г.Теория пограничного слоя: Пер. с нем. – М.:
Наука, 1974. – 712 с.
3. Патанкар С. Численные методы решения задач теплообмена и
динамики жидкости: Пер. с англ.– М.: Энергоатомиздат, 1984.-152 с.
Дополнительная литература
1. Себиси Т., Брэдшоу П. Конвективный теплообмен. Физические
основы и вычислительные методы: Пер. с англ.–М.:Мир, 1987.– 592 с.
2. Трехмерные турбулентные пограничные слои: Пер. с англ./
Под ред. Х. Фернхольца, Е. Краузе. – М.: Мир, 1985. – 384 с.
3. Госмен А.Д., Пан В.М., Ранчел А.К., Сполдинг Д.Б., Вольфштейн М. Численные методы исследования течений вязкой жидкости:
Пер. с англ. – М.: Мир, 1972. – 326 с.
10 семестр
Основная литература
1. Зенкевич О., Морган К. Конечные элементы и аппроксимация:
Пер. с англ.– М.: Мир, 1986. – 318 с.
2. Югов В.П. ANSYS ?.. это очень просто. (Тепломассообмен и
гидрогазодинамика).– М.: Изд-во CAD-FEM, 2000. – 104 с.
3. Югов В.П. Меню утилит и линейка инструментов ANSYS 5.7.1.
– М.: Изд-во CAD-FEM, 2002. – 164 с.
Дополнительная литература
1. Ши Д. Численные методы в задачах теплообмена. – М.:Мир,
1988. – 544 с.
2. Сабонадьер Ж.-К., Кулон Ж.-Л. Метод конечных элементов и
САПР: Пер. с франц.– М.: Мир, 1989. – 190 с.
3. Молчанов И.Н., Николенко Л.Д. Основы метода конечных элементов. – Киев: Наук. Думка, 1989. – 272 с.