Методические указания для решения задач динамического
реклама
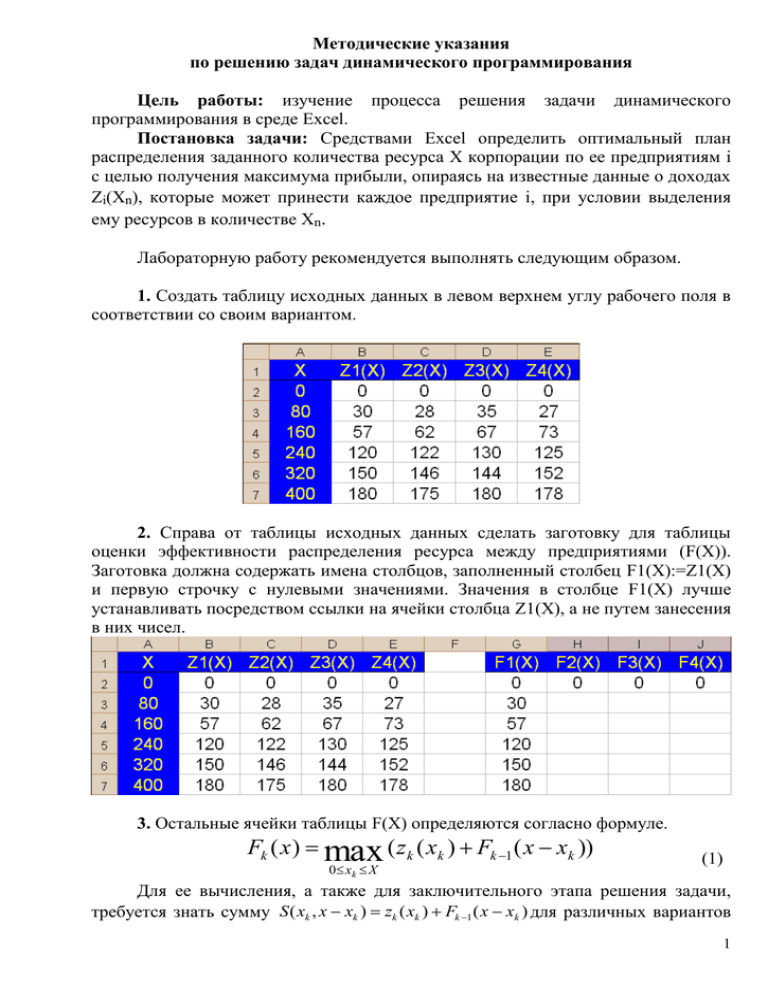
Методические указания по решению задач динамического программирования Цель работы: изучение процесса решения задачи динамического программирования в среде Excel. Постановка задачи: Средствами Excel определить оптимальный план распределения заданного количества ресурса Х корпорации по ее предприятиям i с целью получения максимума прибыли, опираясь на известные данные о доходах Zi(Хn), которые может принести каждое предприятие i, при условии выделения ему ресурсов в количестве Хn. Лабораторную работу рекомендуется выполнять следующим образом. 1. Создать таблицу исходных данных в левом верхнем углу рабочего поля в соответствии со своим вариантом. 2. Справа от таблицы исходных данных сделать заготовку для таблицы оценки эффективности распределения ресурса между предприятиями (F(Х)). Заготовка должна содержать имена столбцов, заполненный столбец F1(X):=Z1(X) и первую строчку с нулевыми значениями. Значения в столбце F1(X) лучше устанавливать посредством ссылки на ячейки столбца Z1(Х), а не путем занесения в них чисел. 3. Остальные ячейки таблицы F(Х) определяются согласно формуле. Fk ( x ) max ( zk ( xk ) Fk 1 ( x xk )) 0 xk X (1) Для ее вычисления, а также для заключительного этапа решения задачи, требуется знать сумму S ( xk , x xk ) zk ( xk ) Fk 1 ( x xk ) для различных вариантов 1 распределения заданного количества ресурса между фиксированным количеством предприятий. Для этого необходимо построить вспомогательные таблицы S (см. далее). 4. Назовем группой предприятий те k-1 предприятий, для которых ранее было вычислено Fk-1(x-xk). Под предприятием будем понимать рассматриваемое в данный момент времени предприятие k. Тогда некоторое количество ресурсов X может быть распределено с шагом ∆ между предприятием и группой предприятий X 1 способами, для каждого из которых необходимо подсчитать сумму S(xk, x-xk). 5. Будем строить таблицы S и F параллельно, следующим образом. Начнем построение с таблицы S(80) – таблицы для вариантов распределения 80-ти единиц ресурсов между N предприятиями. Для 80-ти единиц ресурсов с шагом 80 существует 2 варианта распределения: выделить 0 ресурсов группе предприятий и 80 рассматриваемому предприятию и наоборот, 80 – группе, 0 – предприятию. Занесем варианты распределения в таблицу. Подсчитаем si для двух предприятий (предприятия 2 и группы, в которой только предприятие 1), для чего заведем столбец с заголовком “Z2+F1”. Данный столбец, например, будет иметь ячейки с адресами С13 и С14. В ячейку С13 поместим сумму ячеек С3 и G2 (поскольку Z2(80) хранится в ячейке С3, а F1(0) – в ячейке G2). В ячейку С14 поместим сумму ячеек С2 и G3 (по аналогичным соображениям). Теперь в соответствии с формулой (1) можно определить значение F2(80) – оно равно максимуму среди ячеек C13 и С14. Запишем в ячейку H3 (в которой хранится F2(80)) формулу «макс (С13;C14)». 2 Теперь рассчитаем столбцы “Z3+F2”, “Z4+F3” таблицы S(80) и определим значения F3(80) и F4(80). Сделать это просто, но необходимо строго соблюдать последовательность операций. Поименуем столбцы “Z3+F2” и “Z4+F3”. Теперь выделим ячейки С13, С14 и скопируем их в соседние D13,D14, в результате чего, благодаря средствам автоматизации Excel, получим искомые значения для столбца “Z3+F2”. Теперь необходимо проделать аналогичную процедуру и скопировать ячейку H3 таблицы F в ячейку I3, чтобы рассчитать F3(80). Только после этого можно вернуться к таблице S(80) и рассчитать столбец «Z4+F3» путем копирования ячеек D13,D14 в ячейки E13,E14. Далее необходимо вернуться к заполнению таблицы F и получить значение F4(80) посредством копирования ячейки I3 в ячейку J3. 3 Такая строгая последовательность операций заполнения обусловлена, как Вы знаете, взаимосвязями между ячейками таблиц S и F. 6. Аналогичные процедуры по построению таблиц S(160), S(240), S(320), S(240) и заполнению оставшейся части таблицы F необходимо проделать при распределении 160, 240, 320 и 400 единиц ресурсов. Следует еще раз обратить внимание, что формулы для вычисления значений будут вводиться вручную только для ячеек столбцов Z2+F1 каждой из таблиц S, а также для ячеек столбца F2(X) таблицы F. Остальные ячейки таблиц (кроме исходных данных) вычисляются в процессе копирования одних ячеек в другие. В результате получаем заполненные таблицы: 4 7. После построения всех таблиц можно определить оптимальный план распределения ресурсов, начиная с последнего этапа. Из таблицы F определяем, что максимальная прибыль при распределении ресурсов между 4-мя предприятиями составляет 203. По таблице S(400), находим, что максимальная прибыль за весь рассматриваемый период, равная 203, получается, если 4-му предприятию выделить 160 ресурсов, а остальным 3-м – 240 ресурсов. Возвращаемся к таблице F и определяем, что оптимальное распределение 240 ресурсов между 3мя предприятиями приносит прибыль, равную 130. Далее переходим к таблице S(240), которая отражает распределение 240 ресурсов между 3-им предприятием и группой из 2-х предприятий (т.е. нас интересует распределение внутри группы из 3-х предприятий – столбец Z3+F2), и определяем, что прибыль в 130 единиц может быть получена, если 240 ресурсов целиком отдать 3-му предприятию. 5 7. Таким образом, оптимальное распределение предприятиями при заданных условиях следующее: - предприятию 1 – 0 рес; - предприятию 2 – 0 рес; - предприятию 3 – 240 рес; - предприятию 4 – 160 рес. ресурсов между 4-мя 8. При другой постановке задачи может оказаться, что оптимальное распределение ресурсов подразумевает выделение ресурсов каждому предприятию. В этом случае процесс обратного анализа должен быть продолжен. 6


