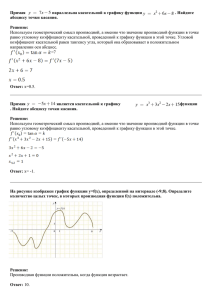
Тема урока: Экстремумы функции 11 класс 14.12.2015г.
реклама

ГБОУ школа №20 Невского района Санкт-Петербурга Тема урока: Экстремумы функции 11 класс 14.12.2015г. На рисунке изображен график функции y= f (x), определенной на интервале (−2; 12). Найдите сумму точек максимума функции f (x). На рисунке изображен график функции y= f (x), определенной на интервале (−2; 12). Найдите сумму точек минимума функции f (x). На рисунке изображен график y= f ' (x) − производной функции f (x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f (x), принадлежащих отрезку [−6; 9]. На рисунке изображен график y= f ' (x) − производной функции f (x), определенной на интервале (−18; 6). Найдите количество точек минимума функции f (x), принадлежащих отрезку [−13; 1]. Максимум a = - 2, b = 6, f (-2) = 1, f ' (x) > 0 при - 2 < х < 1 f ' (x) < 0 при 1 < х < 6 f ' (1) = 0 f (6) = -2 Минимум a = - 4, b = 2, f (-4) = 2, f ' (x) < 0 при - 4 < х < - 1 f ' (x) > 0 при -1 < х < 2 f ' (-1) = 0 f (2) = 1 Максимум Укажите, какому свойству удовлетворяет функция y(x) на отрезке [1;4], если задана ее производная Свойство Имеет Имеет функции Возрастает Постоянна Убывает максимум минимум Производная y' = – 4 y' = 3 – x y' = 1 + 3x y' = 0 y'= 6 Укажите, какому свойству удовлетворяет функция y(x) на отрезке [1;4], если задана ее производная Свойство Имеет Имеет функции Возрастает Постоянна Убывает максимум минимум Производная + y' = – 4 + y' = 3 – x y' = 1 + 3x + + y' = 0 y'= 6 + Минимум Укажите, какому свойству удовлетворяет функция y(x) на отрезке [-3;0], если задана ее производная Свойство Имеет Имеет функции Возрастает Постоянна Убывает максимум минимум Производная y' = – 3 y' = – 2x + 5 y' = 2х + 3 y' = 0 y'= 3х2 + 1 Укажите, какому свойству удовлетворяет функция y(x) на отрезке [-3;0], если задана ее производная Свойство Имеет Имеет функции Возрастает Постоянна Убывает максимум минимум Производная + y' = – 3 y' = – 2x + 5 + + y' = 2х + 3 + y' = 0 y'= 3х2 + 1 + Подведение итогов Домашнее задание стр. 126 № 55 (2), 54 (2), 56 (2) Спасибо за урок!