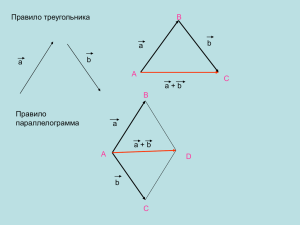
Действия над векторами

Действия над
векторами
 Сложение векторов
 Вычитание векторов
 Умножение вектора
на число
 Сложение

«Правило треугольника»
 Сложение

векторов
векторов
«Правило
параллелограмма»
 Разностью
векторов а и с
называется такой вектор
к, который в сумме с
вектором с дает вектор а
Например: найти разность
векторов е и к
 Суммой
векторов (а;b;с) и (m;n;k) называется
вектор
(a+m;b+n;c+k)
 Например,
если
найти координаты вектора
(-5;3;-9) и
(4; -2; 8)
Решение:
(-5+4; 3+(-2); -9+8)
(-1; 1; 1)
,
А
В
С
М
К
Н
Е
Р
А
В
С
М
К
Н
Е
Р
 Дано:
А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
Определить: пары равных векторов
Решение:
Равны соответствующие координаты у
векторов
,
, значит, они
попарно равны
 Произведением
вектора (а;в;с) на число
λ называется вектор λ (λа; λв; λс)
 Например,
если
Решение:
найти координаты вектора
(5;-1;-2)
,
 Дано:
 Найти:
М. И. Башмаков. Математика.
Учебник
Стр.81, занятие 2