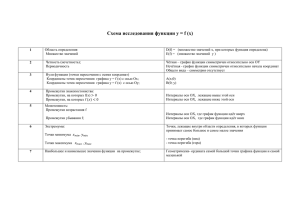
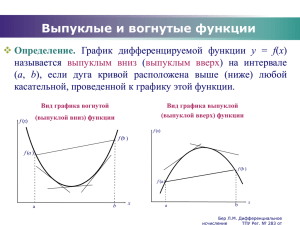
Направления выпуклости графика функции. Точки перегиба

1 вариант
1)  40 х 3  24 х 2  2
2) 8х  cos x
3) 4 х  72 х  10 х
х 6  18 х 2
4) 14
12 х  12 х
5) (6 х  2)
15х  3
6) 15х  6
7) 1030х х 15 х30 х 2
8) 6(5х  8х ) (25х  24х )
9) 6 * ln 6
10) 1,5х  10
9
3
5
4
2
2
2
2
2
3
2
5
3 5
х
1

2
4
2
2 вариант
1)  55х  36 х  9
2)  cos x  26
3) 6х  21х  12х
4) 1224хх  848х х
5) (4х  4)
18 х  6
6) 12 х  12 х  6
7)  8х32х 6х 6 4
8) 3(11х  9х ) (33х  18х)
9) 7 * ln 7
5
10) 3 х  5
10
7
2
4
6
5
3
6
3
3
2
2
3
3
4
3
2 2
х

«5» -без ошибок
«4»-1-3 ошибки
«3»-4-6 ошибок
2
3
2
Направления выпуклости
графика функции:
1. Выпуклость вверх
2. Выпуклость вниз
(вогнутость)
Пример функции, выпуклой вниз (вогнутой):
Пример функции, выпуклой вверх
Если у// = f(х) - положительна, то
график функции является
выпуклым вниз;
Если у// = f(х) - отрицательна, то
график функции является
выпуклым вверх.
1.Найти вторую производную
2. Найти точки, в которых вторая производная
равна нулю или не существует.
3. Найти интервалы, на которые область
определения разбивается этими точками
4. Определить знаки второй производной в
каждом интервале
Если f '‘(х) < 0, то кривая выпукла,
если f '‘(х) > 0 – вогнута
Пример 1. Исследовать на выпуклость график
функции:
f(х) = х3 – 3х2 + 2х + 1
Точка графика, в которой
существует касательная, и при
переходе через которую кривая
меняет свое направление
выпуклости, называется
точкой перегиба.
1. Найти вторую производную
2. Найти критические точки функции
3. Исследовать знак в интервалах, на которые
критические точки делят область определения
функции . Если критическая точка разделяет
интервалы где вторые производные разных
знаков, то является абсциссой точки перегиба
графика функции;
4. Вычислить значения функции в точках
перегиба.
Пример 2. Найти точки перегиба графика
функции:
f(х) = 6 х 2  х 3
Пример 3. Исследовать на выпуклость и найти
точки перегиба графика функции:
f(х)
1 3
= х  2х 2  7х  4
3
Найти интервалы выпуклости и вогнутости и
точки перегиба
Вариант 1
Вариант 2
у = х³ - 12х + 4
у = ¼ х4 – 3/2 х²