Короткий условный оператор

ВЕТВЯЩИЙСЯ АЛГОРИТМ
ЦЕЛИ:
Познакомиться с понятиями: логический тип
данных, ветвящийся алгоритм.
Освоить средства реализации разветвляющихся
алгоритмов на языке Паскаль.
Операции сравнения
Операция отношения
Равно
Не равно
Больше
Больше или равно
Меньше
Меньше или равно
Обозначение
=
<>
>
>=
<
<=
Пример: 3>5 Какое значение имеет результат этого сравнения? Это ложь.
Результат операции сравнения может иметь одно из двух значений: истина
или ложь. В языке программирования Паскаль для хранения в памяти ЭВМ
таких значений используется специальный тип данных, который
называется логическим.
Логический тип данных
К логическому типу относятся данные, которые могут принимать одно из двух
значений: true (истина) или false (ложь). Различают логические константы и
логические переменные.
Описание логического типа данных
Соnst
cl=true;
Var
L, cl : boolean;
Begin
L:=3>5;
Writeln(‘значение логической переменной’,L);
Writeln(‘значение логической константы’,cL);
End.
В языке Паскаль не предусмотрен ввод с клавиатуры данных логического типа, но
существует вывод переменных и констант логического типа, как это показано
в примере.
Условное выражение
Условными выражениями называются такие выражения, которые
содержат арифметические выражения, связанные операциями
сравнения (отношения).
Примеры условных выражений:
(а + b) * с >= 1000;
c * d > x + (y * c) * b.
Результатом условного выражения являются логические величины
false или true. Если условие выполняется, то результатом его
выполнении является значение true, в противном случае - false.
Пример: при а = 4, b = 45 условное выражение а + 16 < b
принимает значение true, а
условное выражение а * а = 100 + b принимает значение false.
Логические операции
Над данными логического типа определены следующие операции:
NOT - логическое НЕ – логическое отрицание;
AND - логическое И – логическое умножение;
OR - логическое ИЛИ – логическое сложение;
XOR - исключающее ИЛИ – исключающее ИЛИ, сложение по
модулю 2.
Операция NOT имеет один операнд, все остальные - два
операнда.
Пример:
NOT A, A OR В. Операнды А и В являются данными логического
типа.
Результаты вычисления логических операций приведены в
таблице 2.2, которая содержит таблицы истинности для всех
описанных выше логических операций.
Результаты логических операций
Логическая операция
NOT
AND
OR
XOR
Значение операнда1
Значение операнда2
Значение результата
TRUE
FALSE
FALSE
TRUE
TRUE
TRUE
TRUE
FALSE
FALSE
FALSE
TRUE
FALSE
FALSE
FALSE
TRUE
FALSE
TRUE
TRUE
TRUE
FALSE
TRUE
TRUE
TRUE
FALSE
TRUE
FALSE
FALSE
FALSE
TRUE
TRUE
FALSE
FALSE
TRUE
TRUE
TRUE
FALSE
TRUE
FALSE
FALSE
FALSE
Логические выражения
Логическое выражение состоит из логических элементов и логических операций. Логическое
выражение, как видно из таблицы 2.2, может принимать одно из двух значений: true или
false. Логический элемент, который согласно таблице 2.2. может принимать одно из двух
значений true или false, должен быть одним из следующих:
- логической константой (true или false);
- логической переменной;
- условным выражением;
- логическим выражением.
Здесь впервые мы встречаемся с рекурсивным определением, понятие логического выражения
вводится через определение логического выражения.
Вычисление значения логического выражения происходит по старшинству операций и его
результатом может быть значение true или false.
В Паскале определены следующие группы приоритетов логических и арифметических операций:
1) Not;
2) *, /, Div, Mod, And;
3) +, -, Or, Xor;
4) =, <>, <, >, <=, >=.
1) Not;
2) *, /, Div, Mod, And;
3) +, -, Or, Xor;
4) =, <>, <, >, <=, >=.
Приоритет операций убывает в указанном порядке, наивысшим приоритетом обладают
операции группы 1, они выполняются первыми при вычислении выражений, а самым
низшим - операции группы 4, они выполняются последними.
Порядок выполнения операций может быть изменен с помощью скобок, так же, как и при
вычислении арифметических выражений.
Пример вычисления логического выражения: (а * b + с = х + y) and (k * b > t)
Пусть а = 3.0, b = 4.1, с = 4, х = 2.5, у = 5, k = 3, t = 10, тогда логическое выражение
вычисляется в следующем порядке:
1) а * b + с равно 16.3;
2) х + у равно 7.5;
3) k * b равно 12.3;
4) (16.3 = 7.5) равно false;
5) (7.5 > 10) равно false;
6) false and false равно false.
Таким образом, результатом вычисления всего выражения будет false.
Логические выражения можно использовать для записи условий, которые применяются в
математике.
Примеры записи условных и
логических выражений
Задача 1. На числовой оси дан отрезок [a,b] и
точка с координатой х. Написать условие:
точка х принадлежит отрезку [a,b].
Решение. В математике такое условие
записывается так: (a≤x≤b). Вычислительная
машина в каждый момент времени выполняет
одно действие и записывает результат этого
действия в память. Поэтому в
программировании это условие записывается
следующим образом: (a≤x)and(x≤b).
Задача 2. На числовой оси дан отрезок [a,b] и
точка с координатой х. Написать условие:
точка х не принадлежит отрезку [a,b].
Решение. В математике такое условие
записывается так: (a>x>b). В
программировании это условие
записывается следующим образом:
(x<a)or(x>b).
Задача 3. На плоскости в декартовой системе
координат задана точка своими
координатами (X, Y) и квадрат со
стороной 2, центр которого расположен в
начале координат. Записать логическое
выражение, вычисляющее, принадлежит
ли точка заштрихованной области.
Решение. Если решать задачу «в лоб», то
алгоритм следует записать следующим
образом.
(1>x>-1), при этом мы выделяем на
координатной плоскости вертикальную
полосу шириной 2 бесконечной длины, И
(1>y>-1), при этом на координатной
плоскости выделяется горизонтальная
полоса шириной 2 также бесконечной
длины. На пересечении этих полос
находится заданная область. Получим
логическое условие (1>x>-1) И (1>y>-1),
которое содержит вычисление 4-х условий
и одной логической операции. Можно
записать решение этой задачи иначе
(│x│<1)И(│y│<1).
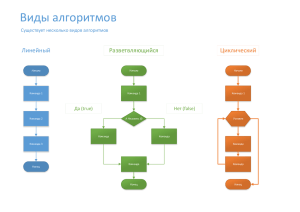
Ветвящийся алгоритм
Организовать ветвление в программе можно двумя
способами: в зависимости от значения условного или
логического выражения или в зависимости от
значения переменной порядкового типа. Ветвление в
зависимости от значения условного или логического
выражения осуществляется с помощью одного из
условных операторов.
В языке Паскаль существует три вида условных
операторов: короткий условный оператор, полный
условный оператор и сложный условный оператор.
Ветвление в зависимости от значения переменной
порядкового типа осуществляется с помощью оператора
выбора. В языке Паскаль определены две
разновидности оператора выбора.
Короткий условный оператор
Короткий условный оператор имеет
следующий синтаксис.
IF <условное или логическое
выражение> THEN <оператор>;
Здесь IF, THEN – ключевые (или
зарезервированные) слова;
<условное или логическое
выражение> - любое условное
или логическое выражение,
отделяется от ключевых слов
пробелами;
<оператор> - простой или
составной оператор языка
Паскаль (кроме условного);
; - разделитель, обозначает конец
оператора.
Начало
ветвления
False
Условн
ое или
логичес
кое
выраже
ние
True
Оператор
Конец
Путь 2
Путь 1
Рисунок 2.1.
Блок-схема
короткого
условного
оператора
Полный условный оператор
Полный условный оператор
имеет следующий синтаксис.
IF <условное или логическое
выражение> THEN <оператор
1>
ELSE <оператор 2>;
Здесь IF, THEN, ELSE – ключевые
(или зарезервированные)
слова;
<условное или логическое
выражение> - любое
условное или логическое
выражение, отделяется от
ключевых слов пробелами;
<оператор 1>, <оператор 2> простой или составной
оператор языка Паскаль
(кроме условного);
; - разделитель, обозначает
конец оператора.
Начало
ветвления
False
Оператор 2
Условно
е или
логическ
ое
выражен
ие
True
Оператор 1
Конец
Путь
2
Рисунок 2.2.
Блок-схема
полного условного
оператора
Путь
1
Сложный условный оператор
Сложным условным
оператором является
один из условных
операторов –
короткий или полный,
в котором <оператор
1> ИЛИ / И <оператор
2>,<оператор>
являются условными
операторами.
Начало ветвления
False
False
Условие 1
True
Условие
False
3
Рисунок 2.3.
Блок-схема сложного
условного оператора
True
Условие
True
2
Оператор 3
Оператор 2
Конец ветвления
Оператор 1
Оператор выбора
В языке Паскаль существуют две разновидности оператора
выбора, которые имеют следующий синтаксис:
CASE <выражение> OF
< константа 1> :
<оператор1>;
< константа 2> :
<оператор 2>;
...
< константа N> :
<оператор N>;
ELSE <оператор>
END;
СASE <выражение> OF
< константа 1> :
<оператор1>;
< константа 2> :
<оператор 2>;
...
< константа N>:
<оператор N>;
END;
Здесь:
CASE, OF, ELSE, END – ключевые (зарезервированные) слова;
<выражение> - в операторе CASE может быть только порядкового типа: целого, символьного,
логического, перечислимого или ограниченного типов. Нельзя использовать вещественный тип
данных;
< константа 1>…< константа N> - конкретные значения <выражения>, которые входят в диапазон
значений типа, к которому принадлежит результат вычисления <выражения>;
<оператор 1>…<оператор N>, <оператор> - любые простые или составные операторы языка Паскаль;
: - разделитель, отделяет значение константы от оператора;
Составной оператор
Составной оператор - это последовательность операторов программы, заключенная в
операторные скобки BEGIN ... END. Для наглядности советуем эти операторные скобки
размещать друг под другом, а последовательность операторов между ними сдвигать вправо.
Среди операторов, входящих в составной оператор, могут быть использованы другие составные
операторы: допускается произвольная глубина их вложенности. Тело вложенного составного
оператора рекомендуем также сдвигать относительно операторных скобок BEGIN и END. В
этом случае запись алгоритма приобретет приблизительно следующий вид:
BEGIN
<оператор 1>;
BEGIN
<оператор2>;
<оператор3 >;
BEGIN
<оператор4>;
<оператор5>;
END
END
END;
Такая форма записи алгоритма позволяет легко ориентироваться в структуре программы и,
следовательно, избегать логических и синтаксических ошибок.
Примеры программ
Задача 1
Для заданного значения X вычислить значение функции F(X) = Y, которая определяется
следующим образом:
В этом алгоритме для организации ветвления можно использовать условие X >= 0. Если это
условие верно, то надо вычислять Y по формуле Y = 4Х, если не верно, то Y = 0.
Var
x,y : real;
Begin
Writeln (' Введите значение X ');
Read(x);
If x >= 0 then y := 4 * x
Else y := 0;
Writeln('y=', y:6:3);
End.
Задача 4.
Два прямоугольника, расположенные в первом квадранте, со сторонами, параллельными осям координат,
заданы координатами своих левого верхнего и правого нижнего углов. Для первого прямоугольника это
точки (xl,yl) и (х2,0), для второго - (хЗ,уЗ), (х4,0).
Составьте алгоритм или напишите программу, определяющую, пересекаются ли данные прямоугольники, и
вычисляющую общую площадь, если они пересекаются.
Алгоритм решения этой задачи может быть записан следующим образом:
Нарисовать первый квадрант декартовой системы координат и пересекающиеся прямоугольники. Обозначить
левую точку пересечения (а, b), правую точку (лежащую на оси X) - (c,d).
Алгоритм решения задачи:
Переменные xl,yl,x2,x3,y3,x4,a,b,c,d,S : тип вещественный;
Ввести xl,yl,x2,y2,x3,y3,x4;
Если у1 или у3 равны 0, то прекратить решение;
Вычислить минимальное из чисел yl и уЗ : b =
min(yl, y3);
Вычислить максимальное из чисел xl и xЗ : a = max (
xl, x3);
Вычислить минимальное из чисел х2 и х4: c =
min(x2,x4);
Присвоить d = 0 (по условию задачи);
Если (а < с) И (b≠0) то начало
Выдать
на
экран
:
«Прямоугольники
пересекаются»;
Вычислить общую площадь S = (c - a) / b;
Выдать на экран S
Конец иначе выдать на экран «Прямоугольники не
пересекаются или касаются».
Программа на языке Паскаль.
Var
X1,y1,x2,y2,x3,y3,x4,a,b,c,d,s:real;
Begin
Write(‘x1=’); readln(x1);{ввод данных}
Write(‘y1=’); readln(y1);
Write(‘x2=’); readln(x2);
Write(‘x3=’); readln(x3);
Write(‘y3=’); readln(y3);
Write(‘x4=’); readln(x4);
If (y1=0)or(y3=0) then begin
Writeln(‘Не верно введены данные’);
Halt; Readln;
End;
If y1<y3 then b:=y1 else b:=y3;
If x1>x3 then a:=x1 else a:=x3;
If x2<x4 then c:=x2 else c;=x4;
D:=0;
If a<c then begin
Writeln(‘Прямоугольники пересекаются’);
S:=(c-a)/b;
Writeln(‘Общая площадь=’,s:0:3);
End;
Readln;
End.
Задача 5.
Дан треугольник ABC с координатами вершин А(Ах,Ау), В(Вх.Ву),
С(Сх.Су), где числа Ах, Ay, Bx, By, Cx, Су - целые. Составьте
алгоритм, определяющий, является ли этот треугольник
равнобедренным. Входные данные задать с помощью датчика
случайных чисел из диапазона [0,20].
Алгоритм решения задачи:
Ввести координаты вершин Ах, Ay, Bx, By, Cx, Су;
Вычислить квадраты длин сторон АВ, ВС и АС по формулам
АВ2 = (Вх-Ах)2 + (Ву-Ау)2;
ВС2 = (Сх-Вх)2 + (Су-Ву)2;
АС2 = (Ах-Сх)2 + (Ay-Су)2;
Ecли АВ2 = ВС2 или ВС2 = АС2 или АВ2 = АС2, то
Вывести на экран "Треугольник ABC равнобедренный" иначе
"Треугольник ABC не равнобедренный".
Программа на языке Паскаль:
Const
Eps=0.00001;
Примечание
Var
В этой задаче впервые встретилась задача сравнения
Ax,Ay,Bx,By,Cx,Cy : Real;
вещественных чисел. Вещественные числа нельзя сравнивать с
AB2,BC2,AC2 : Real; { квадраты сторон }
помощью знака «равно», т.к. эти числа представляются в памяти
машины с некоторой точностью, которая зависит от типа данных.
Begin
Поэтому нужно ввести точность, в нашем примере это константа
Randomize;
eps, и сравнивать по правилу: если модуль разности чисел меньше
Writeln ('Координаты точки А ');
точности, то числа равны.
Ax:=random(20)+random;
Ay:=random(20)+random;
Writeln(‘Ax=’,Ax:0:2,’Ay’,Ay:0:2);
Writeln ('Координаты точки В ');
Bx:=random(20)+random;
By:=random(20)+random;
Writeln(‘Bx=’,Bx:0:2,’By’,By:0:2);
Writeln ('Координаты точки С ');
Cx:=random(20)+random;
Cy:=random(20)+random;
Writeln(‘Cx=’,Cx:0:2,’Cy’,Cy:0:2);
AB2 := sqr(Ax - Bx) + sqr(Ay - By);
BC2 := sqr(Cx - Bx) + sqr(Cy - By);
AC2 := sqr(Ax - Cx) + sqr(Ay - Cy);
if (abs(АВ2 - ВС2)<eps) or (abs(AC2 - BC2)<eps) or (abs(AB2 - AC2)<eps) then Writeln ('Треугольник равнобедренный ')
else Writeln (Треугольник не равнобедренный ');
End.