logoperacii
реклама

Тема:
Понятие высказывания.
Основные логические
операции.
Высказывания и
высказывательные формы
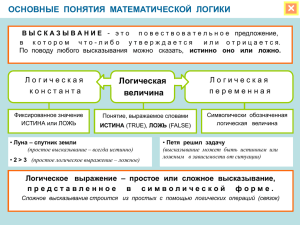
Высказывание — это любое предложение
какого-либо языка (утверждение),
содержание которого можно определить
как истинное или ложное.
Всякое высказывание или истинно, или ложно;
быть одновременно и тем и другим оно не
может.
Примеры высказываний:
• 1) {Город Вашингтон — столица США}
(истинное высказывание);
• 2) {Число 2 является делителем числа 7}
(ложное высказывание);
• 3) {3 + 5 = 2 4} (истинное высказывание);
• 4) {2 + б > 10} (ложное высказывание);
• 5) {II + VI > VIII} (ложное высказывание);
• 6) {Сумма чисел 2 и 6 больше числа 8}
(ложное высказывание);
• 7) {Two plus six is eight} (истинное
высказывание);
• 8) {Na — металл} (истинное высказывание).
Высказывание называется простым
(элементарным), если никакая его часть сама
не является высказыванием. Если это условие
не выполняется, высказывание называется
сложным.
Они обозначаются заглавными латинскими
буквами:
А = {Аристотель — основоположник логики}.
В = {На яблонях растут бананы}.
Примеры сложных высказываний:
1) {В автобусе можно доехать до школы и
почитать журнал};
2) {Число 376 четно или двузначно};
3) {Неверно, что Солнце движется вокруг
Земли};
4) {Если сумма цифр числа делится на 3, то
число делится на 3}.
А = {Аристотель — основоположник логики}.
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в
соответствие 1, ложному — 0.
Таким образом, А = 1, В = 0.
Обоснование
истинности
или
ложности
простых высказываний решается вне алгебры
логики.
Например,
истинность
или
ложность
высказывания «Сумма углов треугольника
равна
180
градусам»
устанавливается
геометрией, причем в геометрии Евклида это
высказывание является истинным, а в
геометрии Лобачевского — ложным.
Логические операции
Конъюнкция — это логическая операция,
ставящая в соответствие каждым двум
элементарным
высказываниям
новое
высказывание, являющееся истинным тогда и
только
тогда,
когда
оба
исходных
высказывания
истинны.(логическое
умножение)
Таблица истинности конъюнкции
A
B
AB
0
0
0
0
1
0
1
0
0
1
1
1
Дизъюнкция — это логическая операция,
которая
каждым
двум
элементарным
высказываниям ставит в соответствие новое
высказывание, являющееся истинным тогда и
только тогда, когда хотя бы одно из двух
образующих его высказываний истинно.
(логическое сложение)
Таблица истинности дизъюнкции
A
0
0
1
1
B
0
1
0
1
AB
0
1
1
1
Строгая дизъюнкция (двойное «или»),
которой
в
естественном
языке
соответствует связка «либо..., либо...»).
A
0
0
1
1
B
0
1
0
1
AB
0
1
1
0
Импликация — это логическая операция,
ставящая в соответствие каждым двум
элементарным
высказываниям
новое
высказывание, являющееся ложным тогда и
только
тогда,
когда
условие
(первое
высказывание) истинно, а следствие (второе
высказывание) ложно (логическое следование).
Таблица истинности импликации
A
0
0
1
1
B
0
1
0
1
AB
1
1
0
1
Эквиваленция — это логическая операция,
ставящая в соответствие каждым двум
элементарным
высказываниям
новое
высказывание, являющееся истинным тогда и
только
тогда,
когда
оба
исходных
высказывания одновременно истинны или
одновременно ложны. (равнозначность)
Таблица истинности эквиваленции
A
0
0
1
1
B
0
1
0
1
AB
1
0
0
1
Отрицание — это логическая операция,
которая каждому данному высказыванию
ставит в соответствие новое высказывание,
которое истинно, если данное высказывание
ложно, и ложно, если данное высказывание
истинно. (инверсия)
Таблица истинности отрицания
A
А
0
1
1
0
Логические операции
имеют следующий
приоритет:
действия в скобках,
отрицание, , v,
=>,<=>.