Графический способ решения уравнений и систем уравнений с

« Считать несчастным тот день или тот час, в который ты не
усвоил ничего нового, ничего не прибавил к своему образованию»
Ян Амос Коменский
1.Рассмотреть и изучить графический способ решения уравнений
и систем уравнений с параметрами.
2.Показать применение данных способов при решении заданий
ГИА и олимпиадных заданий.
3.Подобрать тренировочные задания для отработки метода
решения с помощью движущихся графиков.
Выше изложенное обусловило проблему исследования,
которая заключается в исследовании целесообразности и
возможности изучения методов решения уравнений, содержащих
параметры.
Решение задач с параметрами вызывают большие трудности у
учащихся.
1)Анкетирование : с какими проблемами сталкиваются учащиеся
при подготовке к ГИА. Выявила, что большинство затрудняются
в решении уравнений с параметрами.
2)Изучила теоретический материал по данной теме.
3)Выделила различные способы решения уравнений с
параметрами.
4)Определила более наглядный метод.
5)Научилась решать уравнения с параметрами.
6)Создала медиаресурс для решения уравнений с параметрами.
Аннотация
Тема моей работы «Решение уравнений и систем уравнений с параметром». В
учебном курсе алгебры задач с параметром нет. Мы их рассматривали на
элективном курсе. Они привлекли моё внимание своей необычностью,
разнообразием способов и приёмов решения, возможностью решения одного и
того же уравнения или системы уравнений, содержащих параметр, различными
методами.
Готовя данную работу, я ставила цель более глубокого изучения этой темы,
выявления наиболее рационального решения, быстро приводящего к ответу.
Нельзя научиться решать любые задачи с параметрами, используя какой-то
алгоритм или формулы. При решении задач с параметрами надо всегда активно
использовать соображения, исходящие из здравого смысла. На мой взгляд,
графический метод является удобным и быстрым способом решения уравнений и
систем уравнений с параметрами.
В моей работе рассмотрены типы уравнений и систем из сборника заданий для
подготовки к ГИА по алгебре 2011 года под редакцией Ф. Ф. Лысенко, С. Ю.
Кулабухова. Я надеюсь, что знания, полученные мною в процессе работы,
помогут мне при сдаче экзамена по алгебре в новой форме. Кроме того, решение
заданий такого типа способствует развитию математических навыков,
необходимых для дальнейшего изучения заданий с параметром в старших
классах. И ещё, что немало важно, я научилась выполнять анимацию графиков
функций в Power Point. Это интересно, увлекательно.
Пример 1
При каком значении параметра k система уравнений
у = х² +1
х² +у² = k
имеет единственное решение.
Построим график функции
а) у=х2+1
Это квадратичная функция, график –парабола с вершиной
(0;1) , ветви которой направлены вверх.
б)уравнение х² +у² = k описывает окружность с радиусом
R=k, центром (0;0). С изменением параметра k радиус
окружности также меняется.
Система имеет столько решений, сколько общих точек имеют
графики. Графики могут не иметь общих точек, иметь одну,
две общие точки. Выберем то значение параметра k, при
котором графики имеют одну общую точку, а значит
система имеет единственное решение.
Система
у = х² +1
х² +у² = k
имеет единственное
решение, если k = 1.
Ответ: k = 1.
Пример 2
При каком значении параметра а ,уравнение | х2-4x+3|
имеет три корня.
Построим графики функций: у =|х2-4x+3| и у = а.
а) график функции у =|х2-4x+3| получается в результате
симметричного отображения графика функции у=х2-4x+3
симметрично относительно оси Ох.
б) графиком функции у = а является прямая, параллельная
оси Ох, проходящая через точку (0;а).
С изменением параметра а, прямая перемещается вдоль
оси Оу, параллельно оси Ох. Уравнение имеет столько
решений, сколько общих точек имеют графики. Графики
могут не иметь общих точек, две или три общие точки.
Выберем те значения параметра а ,при котором графики
имеют три общие точки, а значит уравнение имеет три
решения.
При а = 1 графики
имеют три общие
точки, а значит
уравнение имеет
три решения.
Ответ: 1.
Пример 3
При каком значении параметра а ,уравнение х2-4|x|+3 имеет
два корня.
Построим графики функций: у=х2-4x+3, х ≥ 0,
у=х2+4x+3 , х <0
у = а.
а) график функции у =|х2-2x-3| получается в результате
симметричного отображения графика функции у=х2-2x-3
симметрично относительно оси Оу.
б) графиком функции у = а является прямая, параллельная оси
Ох, проходящая через точку (0;а).
С изменением параметра а, прямая перемещается вдоль оси
Оу, параллельно оси Ох. Уравнение имеет столько решений,
сколько общих точек имеют графики. Графики могут не иметь
общих точек, иметь одну , две или три общие точки. Выберем те
значения параметра а ,при котором графики имеют две общие
точки, а значит уравнение имеет два решения.
При а=-1 и а ( 3;+∞)
графики имеют две
общие точки, а
значит уравнение
имеет два решения.
Ответ: {-1} U ( 3;+∞)
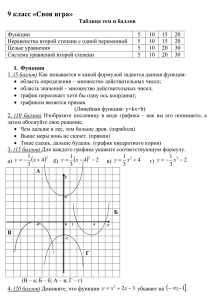
Пример 4
При каких значениях а прямая у = а имеет две общие точки с
графиком функции у = f(x),
x(x-4), если x ≥ 0,
где f(x) =
x(4-x), если x < 0.
С изменением параметра а, прямая перемещается вдоль оси
Оу, параллельно оси Ох. Графики могут иметь одну , две или три
общие точки. Выберем те значения параметра а ,при котором
графики имеют две общие точки.
Построим график функции
x(x-4), если x ≥ 0,
f(x)=
x(4-x), если x < 0.
f(x)=
f(x)=
x²-4x, если x ≥ 0,
4x-x², если x < 0.
(x-2)²-4, если x ≥ 0,
-(x-2) ²+4, если x < 0.
Прямая у = а параллельна оси
Ох. Она будет иметь две
общие точки с графиком
функции у = f(x) при а = 0 и
а = -4.
Ответ: -4; 0.
Пример 5
Найти все значения а, при которых уравнение
(a+4x-x²-1)(a+1-|x-2|) = 0 имеет ровно три корня?
Данное уравнение равносильно совокупности
a - x² + 4x - 1 = 0
a - |x - 2| + 1=0
Выражая параметр а, получаем:
a = x² - 4x + 1
a = |x-2| - 1
График этой
совокупности –
объединение уголка
и параболы.
Прямая а = -1
пересекает
полученное
объединение в трех
точках.
Ответ: -1.
Пример 6
При каком значении параметра b система уравнений
х² + у=b,
х² + у² =9
имеет три решения.
Построим график функции: у = -х² +b и график уравнения
х² + у² =9
а) графиком функции у = -х² +b является парабола, ветви
направлены вниз.
б) а)уравнение х2+у2=9 описывает окружность с радиусом R=3,
центром (0;0).
С изменением параметра b, парабола перемещается вдоль оси
Оу. Система имеет столько решений, сколько общих точек имеют
графики. Графики могут не иметь общих точек, иметь одну , две
или три общие точки. Выберем те значения параметра b ,при
котором графики имеют три общие точки, а значит система
имеет три решения.
При b=3
графики имеют
три общие
точки, а значит
уравнение
имеет три
решения.
Ответ: b= 3.
1. Найдите все значения параметра а при которых система
х² + у² = 1,
х +у = а
имеет единственное решение.
2. При каком значении параметра а система
уравнений
х² + у² =3,
у –х² = а
имеет :а ) одно решение; б) три решения.
Итоги исследования:
Изучив графический способ решения
уравнений и систем уравнений с
параметром, можно сделать вывод, что
применение данных способов решения
является наглядным образцом для
учащихся, интересным и актуальным при
решении заданий ГИА и олимпиадных
заданий.
Список используемой
литературы:
Алгебра: Учебное пособие для учащихся 9 класса с углубленным
изучением математики [Текст] / Н.Я. Виленкин, Т.С. Сурвилло,
А.С. Симонов, А
Галицкий, М.Л. Сборник задач по алгебре для 8-9 классов [Текст]:
уч.пособие для учащихся школ и классов с углубленным
изучением математики / М.Л. Галицкий, А.М. Гольдман, Л.И.
Звавич. – М.: Просвещение, 1994. – 271 с.
Алгебра: Учебное пособие для учащихся 9 класса с углубленным
изучением математики [Текст] / Н.Я. Виленкин, Т.С. Сурвилло,
А.С. Симонов, А
Галицкий, М.Л. Сборник задач по алгебре для 8-9 классов [Текст]:
уч.пособие для учащихся школ и классов с углубленным
изучением математики / М.Л. Галицкий, А.М. Гольдман, Л.И.
Звавич. – М.: Просвещение, 1994. – 271 с.