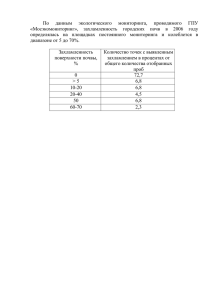
ПараÐ

Дипломная работа Преснова И.М
Научный руководитель Демьянович Ю. К
.
2011


Основная цель –решение уравнение БлэкаШоулза разностными методами,
имплементация на языке С++,
распараллеливание решения с помощью
технологии CUDA, применение к решению
методов автоматического
дифференцирования.
Ожидаемый результат:
Ускорение процесса без потери точности по
сравнению с уже существующими решениями

Модель Блэка-Шоулза:
Mu=0.5 s2 σ2 uss + r s us – ru + ut
(1)
Уравнение: Mu=0;
u(s,t) – искомая функция. Ответом будут являться
значения u при t=0;
Входные параметры:
r –константа из [0,1)
σ – функция от s и t
s ∈ [b,8b], t ∈ [0,T]
к, b, T – положительные константы: к<b
u(b,t)=0, ∀ t ∈ [0,T)
u(S,T)= S – K ,
uss (8b,t) = 0 , ∀ t ∈ [0,T)

Для решения была использована явнонеявная схема Кранка-Николсона,
поскольку она имеет наибольшую точность
решения и устойчива для любых шагов по t
и s( в силу своей неявности).


Разбиения по осям:
По S : наиболее важным является изменение
функции в окрестностях b, поскольку там
находится «тяжело усваиваемое» условие,
поэтому по S берется экспоненциальное
распределение со сгущением уb.
По t : равномерное разбиение





При сравнении с уже существующими
аналитическими решениями* данной модели
отличия в решениях были следующие:
При минимальных размерах сетки:
При S>>B: погрешность порядка 0.01 %
При S близких к B (у нижнего граничного
условия): погрешность порядка 1 %
При увеличении сетки погрешность
уменьшается.
* - реализация модели Эрикса Персона.


На практике кроме значений самой
функции u , так же важно получить ее
производные (первого и второго порядка
по осям t, r, s, σ).
Для их быстрого вычисления применяются
методы автоматического
дифференцирования.


Для получение производных
использовалась технология ускоренного
вычисления производных модели БлэкаШоулза, разработанное шведским
университетом OOPS.
Эта технология позволяет получать
производную, на каждом шаге по времени,
используя значения производной на
предыдущем шаге (эта операция намного
дешевле по времени, чем на каждой
итерации вычислять производную заново)




Для распараллеливания модели применялась
видео карта Nvidia Quadro 600 и библиотека
для работы с ГПУ «CUDA Nvidia toolkit 3.2»
Для сравнения, НЕ-параллельная модель
запускалась на машине со следующими
данными:
CPU(s): 1 x Quad core Intel Core i7 920 2.67 GHz
RAM: 6 Gb
HDD(s): 750 GB SATA
OS: CentOS 5.5 x86_64


В решении данной модели будет
использовано распараллеливание задачи.
Это очень удобно, поскольку так
достигается наибольшая эффективность
ГПУ, чем при распараллеливании по
данным.
Так же распараллеливание по данным
проблематично, поскольку память на ГПУ
сильно ограничена.

Применение к разностным методам.
Алгоритм решения задачи Блэка-Шоулза с
помощью разностных методов сводится к
следующему алгоритму:
 Построение СЛАУ ,
 Решение СЛАУ,
 Вычисление производных из полученных
значений,
 Переход к следующему шагу.
На ГПУ i-ый процесс работает со
значениями, имеющими i-ый индекс, таким
образом при вычислении СЛАУ– вычисляет
только свое уравнение.
При нехватке доступных процессов, каждый
процесс может оперировать за несколько
индексов.




Для решения СЛАУ на ЦПУ применялся
метод прогонки.
Для ГПУ был выбран другой алгоритм
решения СЛАУ: cyclic reduction.
На ЦПУ этот алгоритм работает за 75%
времени работы обычного алгоритма
прогонки.
При переносе на ГПУ – ускорение между
разностной схемой на ЦПУ и на ГПУ
составило 2-2.5 раза (в пользу ГПУ,).
◦ Решаемая задача применяется для вычисления
финансовых объектов.
В реальной ситуации данные для задач поступают в
количестве нескольких тысяч за короткий промежуток
времени.
◦ Полученные данные можно разделить на семейства по
совпадающим входным данным. Поэтому решение сетки
для множества значений S является эффективной
стороной разностного решения модели. Аналитические
решения в своем большинстве решают модель для
одного значения S (что означает что для решение всего
комплекса данных для всех значений S требует
применения этого решения в цикле или распределение
на параллельные процессы)





Эрикс Персон «turbo warrants pricing»
Wikipedia.org
Nvidia “Cuda programming guide”
W. Tucker “Autovalidating numerical
methods”
D. Eglof “High performance finite difference
PDE solvers on GPU”