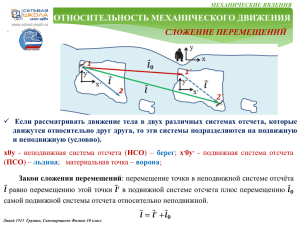
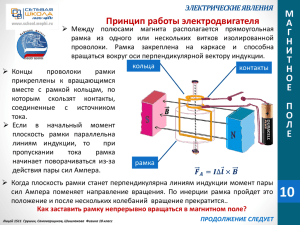
Механические явления
реклама

МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ Работа силы тяжести может быть представлена как убыль потенциальной энергии в поле тяжести 𝑨𝒈 = 𝒎𝒈 𝒉𝟏 − 𝒉𝟐 = 𝚷𝟏𝒈 − 𝚷𝟐𝒈 Работа силы упругости может быть представлена как убыль потенциальной энергии пружины 𝒌𝒙𝟐𝟏 𝒌𝒙𝟐𝟐 𝑨у = − = 𝚷𝟏у − 𝚷𝟐у 𝟐 𝟐 ТЕОРЕМА О ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ (ТоПЭ) Работа консервативной потенциальной энергии Лицей 1511 Грушин, Самоварщиков Физика 10 класс силы равна убыли соответствующей МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ КИНЕТИЧЕСКАЯ ЭНЕРГИЯ Кинетической энергией материальной точки называется скалярная положительная величина, равная половине произведения массы тела на квадрат его скорости. 𝒎𝒗𝟐 𝑲= 𝟐 Кинетическая энергия обозначается символом 𝑲 или 𝑾𝐊 , или 𝑬𝐊 . Размерность кинетической энергии такая же, как и у работы и потенциальной энергии [П] = Дж Кинетическая энергия всегда ≥ 𝟎 Кинетическая энергия - это энергия движущегося тела ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ (ТоКЭ) Приращение кинетической энергии тела (точки) в некотором процессе равно сумме работ всех сил, действовавших на это тело в течение этого процесса 𝒎𝒗𝟐𝟐 𝒎𝒗𝟐𝟏 − = 𝑲𝟐 − 𝑲𝟐 = 𝑨𝑭𝟏 +𝑨𝑭𝟐 + ⋯ + 𝑨𝑭𝒏 𝟐 𝟐 Лицей 1511 Грушин, Самоварщиков Физика 10 класс МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Совершенная силой работа 𝑨𝑭 : - может придать телу массой m скорость 𝒗; - может поднять тело массой m на высоту h ; - может сжать (растянуть) пружину, Механической энергией называется энергия механического движения взаимодействия тел. Она равна сумме кинетической и потенциальной энергий. Кинетическая и потенциальная энергии являются видами механической энергии Лицей 1511 Грушин, Самоварщиков Физика 10 класс и МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ РЕШЕНИЕ ЗАДАЧ 7.7. Шайбу толкнули вверх по шероховатой наклонной плоскости с углом 𝛼 = 30° при основании с начальной скоростью 𝜐0 = 4 м/с . Пройдя расстояние 𝑠 = 1 м , шайба остановилась. Соскользнет ли она вниз?. Изобразим движение шайбы в 𝛼 = 30° 𝜐0 = 4м/с 𝑠 = 1м 𝜐 =? Запишем краткое условие : В точке 2 с координатой 𝑠 шайба остановилась 𝑭тс s Изобразим силы, действующие на шайбу в процессе движения 𝛼 Силу тяжести 𝒎𝒈 Силу трения скольжения 𝑵 у 1 0 Силу реакции опоры 𝒗𝟎 𝛼 системе координат х0у 2 𝒗𝟏 = 𝟎 х 𝟐 𝟐 𝒎𝒗 𝒎𝒗 𝟏 𝟎 В соответствии с ТоКЭ − = 𝑨𝒈 + 𝑨𝑵 + 𝑨𝑭тс ∗ В соответствии с ТоПЭ 𝟐 𝟐 Работа консервативной силы 𝑨𝒈 = 𝚷𝟏𝒈 − 𝚷𝟐𝒈 𝑨𝑵 = 0; 𝑨𝑭тс = −𝐹тс ∙ 𝑠 = −𝜇𝑁 ∙ 𝑠 = −𝜇𝑚𝑔 ∙ 𝑐𝑜𝑠𝛼 ∙ 𝑠 равна убыли соответствующей = 0 − 𝑚𝑔𝑠 ∙ 𝑠𝑖𝑛𝛼; 2 2 𝑚𝑣0 𝑣 0 потенциальной Подставим в ∗ → − = −𝑚𝑔𝑠 ∙ 𝑠𝑖𝑛𝛼 − 𝜇𝑚𝑔 ∙ 𝑐𝑜𝑠𝛼 ∙ 𝑠 → 𝜇𝑔𝑠 𝑐𝑜𝑠𝛼энергии = − 𝑔𝑠 𝑠𝑖𝑛𝛼 → 2 2 2 Определим коэффициент трения Лицей 1511 Грушин, Самоварщиков Физика 10 класс 𝑣0 𝜇= − 𝑡𝑔𝛼 ∗∗ 2𝑔𝑠 𝑐𝑜𝑠𝛼 ПРОДОЛЖЕНИЕ СЛЕДУЕТ МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ПРОДОЛЖЕНИЕ РЕШЕНИЕ ЗАДАЧ 7.7. Шайбу толкнули вверх по шероховатой наклонной плоскости с углом 𝛼 = 30° при основании с начальной скоростью 𝜐0 = 4 м/с . Пройдя расстояние 𝑠 = 1 м , шайба остановилась. Соскользнет ли она вниз?. у Изобразим возможное движение 𝑵 шайбы в системе координат х0у 𝑭 2 тс 𝛼 = 30° Запишем уравнение динамики в 𝜐0 = 4м/с проекции на ось 0х 𝑠 = 1м 0𝑥│𝑚𝑎𝑥 = 𝑚𝑔 ∙ 𝑠𝑖𝑛𝛼 − 𝐹тс → 𝜐 =? 𝒎𝒈 𝛼 0 х 0𝑥│𝑚𝑎𝑥 = 𝑚𝑔 ∙ 𝑠𝑖𝑛𝛼 − 𝜇𝑁 → 0𝑥│𝑚𝑎𝑥 = 𝑚𝑔 ∙ 𝑠𝑖𝑛𝛼 − 𝜇𝑚𝑔 ∙ 𝑐𝑜𝑠𝛼 Подставим из ∗∗ значение коэффициента трения и определим величину 𝑎𝑥 Если 𝑎𝑥 > 0, то шайба соскользнёт с плоскости. Если 𝑎𝑥 ≤ 0, то шайба останется в точке 2 𝑎𝑥 = 𝑔 𝑠𝑖𝑛𝛼 − 𝜇𝑔 𝑐𝑜𝑠𝛼 = 𝑣02 𝑎𝑥 = 𝑔 𝑠𝑖𝑛𝛼 − 𝜇𝑔 𝑐𝑜𝑠𝛼 = 𝑔 𝑠𝑖𝑛𝛼 − 𝑔 𝑐𝑜𝑠𝛼 − 𝑡𝑔𝛼 = 2𝑔𝑠 𝑐𝑜𝑠𝛼 4∙4 4,9 − 8,49 0,943 − 0,577 = = 9,8 ∙ 0,5 − 9,8 ∙ 0,866 − 0,577 2 ∙ 9,8 ∙ 1 ∙ 0,866 = = 1,79м/с2 > 0 → шайба соскользнёт Лицей 1511 Грушин, Самоварщиков Физика 10 класс Ответ: шайба соскользнёт МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ РЕШЕНИЕ ЗАДАЧ 7.16. Проволока изогнута по дуге окружности радиуса 𝑅 (см. рисунок). На проволоку надета бусинка, которая может без трения перемещаться вдоль проволоки. В начальный момент бусинка находилась внизу в точке О. Какую горизонтальную скорость 𝜐 надо сообщить бусинке, чтобы, пройдя часть пути в воздухе, она попала на проволоку в точке В? Угол между ВС (АС) и вертикалью равен 𝛼. 𝛼 𝑅 𝜐 =? 𝒎𝒈 В А 𝛼 Запишем краткое условие : Изобразим силы, действующие на бусинку в процессе движения Изобразим движение бусинки по дуге от начального положения О к конечному А Сила тяжести Сила реакции опоры С 𝒎𝒗𝟐А 𝒎𝒗𝟐О 𝑵 − = 𝑨𝒈 + 𝑨𝑵 В соответствии с ТоКЭ 𝟐 𝟐 О В соответствии с ТоПЭ 𝑨𝒈 = 𝑚𝑔ℎ𝑂 − 𝑚𝑔ℎ𝐴 = 0 − 𝑚𝑔 𝑅 + 𝑅 𝑐𝑜𝑠𝛼 𝑅 Работа силы реакции опоры на траектории от O до А 𝑨𝑵 = 𝟎 , т.к. сила 𝑵 перпендикулярна перемещению в любой точке траектории Следовательно: 𝑚𝑣А2 𝑚𝑣О2 = − 𝑚𝑔𝑅(1 + 𝑐𝑜𝑠𝛼) → 2 2 Лицей 1511 Грушин, Самоварщиков Физика 10 класс 𝑣А2 = 𝑣О2 −2𝑔𝑅(1 + 𝑐𝑜𝑠𝛼) ∗ ПРОДОЛЖЕНИЕ СЛЕДУЕТ МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ПРОДОЛЖЕНИЕ РЕШЕНИЕ ЗАДАЧ 7.16. Проволока изогнута по дуге окружности радиуса 𝑅 (см. рисунок). На проволоку надета бусинка, которая может без трения перемещаться вдоль проволоки. В начальный момент бусинка находилась внизу в точке О. Какую горизонтальную скорость 𝜐 надо сообщить бусинке, чтобы, пройдя часть пути в воздухе, она попала на проволоку в точке В? Угол между ВС (АС) и вертикалью равен 𝛼. 𝛼 𝑅 𝜐 =? Скорость бусинки в точке А 𝒗𝑨 направлена под углом 𝛼 к горизонту 𝒗𝑨 𝛼 С момента отрыва от проволоки бусинка находится в условиях свободного падения – движения под действием 0 В А только силы тяжести 𝒎𝒈 𝛼 Запишем уравнения её движения в проекциях на оси 0х и 0у : 𝑅 𝑡2 С 0𝑥│𝑥 𝑡 = 𝑣А 𝑐𝑜𝑠𝛼 ∙ 𝑡 1 0𝑦│𝑦 𝑡 = 𝑣А 𝑠𝑖𝑛𝛼 ∙ 𝑔 2 2 При 𝑡 = 𝜏 бусинка должна достичь точки В, т.е. 𝑥 𝜏 = 𝑅 𝑠𝑖𝑛𝛼 + 𝑅 𝑠𝑖𝑛𝛼 𝑦 𝜏 = 0 2𝑣А 𝑠𝑖𝑛𝛼 Из 2 следует время полета: 𝜏 = Подставим в 1 следует дальность полета 𝑔 2𝑣А 𝑠𝑖𝑛𝛼 𝑅𝑔 2𝑅 𝑠𝑖𝑛𝛼 = 𝑣А 𝑐𝑜𝑠𝛼 → 𝑣А2 = Из выражения ∗ следует 𝑣02 = 𝑣А2 +2𝑔𝑅 1 + 𝑐𝑜𝑠𝛼 = 𝑔 𝑐𝑜𝑠𝛼 𝑅𝑔 1 = + 2𝑔𝑅 1 + 𝑐𝑜𝑠𝛼 → 𝑣0 = 𝑅𝑔 2 + 2 𝑐𝑜𝑠𝛼 + 𝑐𝑜𝑠𝛼 𝑐𝑜𝑠𝛼 Ответ: 𝑣 = 𝑅𝑔 2 + 2 𝑐𝑜𝑠𝛼 + 1 0 𝑐𝑜𝑠𝛼 𝑦 𝑥 Лицей 1511 Грушин, Самоварщиков Физика 10 класс