Аорта - Санкт-Петербургский политехнический университет
реклама

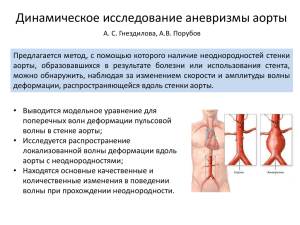
Санкт-Петербургский политехнический университет Петра Великого Институт прикладной математики и механики Кафедра теоретической механики ДИССЕРТАЦИЯ на соискание ученой степени МАГИСТРА Тема: «Динамическое исследование аневризмы аорты» Выполнила Студентка гр. 63604/1 Гнездилова А. С. Руководитель Дфмн, профессор Порубов А.В. Аорта и заболевания аорты Аорта – самый крупный артериальный сосуд в теле человека, от которого отходят все артерии, образующие большой круг кровообращения Рис. 1. Аневризма брюшной аорты Стент — специальная, изготовленная в форме цилиндрического каркаса упругая металлическая или пластиковая конструкция, которая помещается в просвет полых органов и обеспечивает формирование нормальных стенок сосуда (рис.2) Рис. 2. Стентирование аорты Наблюдение волн в аорте Скорость см/сек Давление мм рт. ст. Рис.3. Локализованный и нелинейный характер волны в аорте собаки (Yomosa, 1987) Цели работы: • Исследовать эволюцию нелинейных локализованных волн в аорте; • Исследовать возможность использования этих волн для акустодиагностики неоднородностей на стенке аорты. Поставленные задачи: • Получить модельное уравнение для поперечных волн деформации пульсовой волны в стенке аорты; • При помощи программы Вольфрам Математика разработать код для численного исследования распространения локализованной волны деформации вдоль аорты с неоднородностями; • Установить основные качественные и количественные изменения в поведении волны при прохождении неоднородности. Постановка задачи: Модель • Аорта - цилиндрическая упругая тонкостенная трубка; x Рис. 4. Схематическое изображение трубки • Кровь внутри аорты - идеальная несжимаемая жидкость; • Для простоты рассматривается одномерная постановка задачи на основании ранее разработанной модели (Yomosa, 1987). Постановка задачи: уравнения Для жидкости внутри аорты справедливо уравнение движение в форме уравнения Эйлера: 𝜕𝑣 𝜕𝑣 1 𝜕𝑝 +𝑣 = − , (1) 𝜕𝑡 𝜕𝑥 𝜌 𝜕𝑥 где 𝑣 𝑥, 𝑡 – скорости потока жидкости вдоль оси трубки, 𝜌 – постоянная плотность жидкости, 𝑥 – координата вдоль оси трубки, 𝑡 – время, 𝑝(𝑥, 𝑡) – давление жидкости. Уравнение неразрывности с учетом переменного радиуса для площади поперечного сечения трубки 𝑆 𝑥, 𝑡 = 𝜋 (𝑅 + 𝑢)2 : 1 𝑢𝑡 + 𝑣 𝑅 + 𝑢 𝑥 + 𝑅 + 𝑢 𝑣𝑥 = 0, 2 (2) где 𝑢(𝑥, 𝑡) – радиальное упругое смещение стенки трубки, 𝑅 = 𝑅(𝑥) - радиус трубки Уравнение движения для сдвиговых волн для описания деформационных процессов в 𝑢 𝑢 стенке для внешнего радиального напряжения 𝜎𝑟 = 𝐸 𝑅 1 + 𝑎 𝑅 : 𝜕2 𝑅 + 𝑢 ℎ 𝜌0 𝐻 = 𝑃 − 𝑃 − 𝜎, 0 𝜕𝑡 2 𝑅+𝑢 𝑟 (3) где 𝐸 - модуль Юнга, а параметр 𝑎 характеризует нелинейную упругость, 𝑃 - внешнее давление , 𝑃0 - атмосферное давление, 𝜌0 - плотность материала стенки, константы ℎ и 𝐻 пропорциональны толщине стенки и учитывают ее тканевую структуру Постановка задачи: модельное уравнение В известных работах рассматривались случаи постоянной величины радиуса 𝑅 (Yomosa, 1987) и переменного радиуса 𝑅(Kraenkel et al., 2007). Мы будем рассматривать случай резких изменений, которому соответствует кусочно-непрерывный характер радиуса, при этом производные от радиуса в уравнениях учитываться не будут. После ряда преобразований окончательное новое модельное уравнение в виде модифицированного уравнения Буссинеска с пременными коэффициентами: 𝐸ℎ0 1 𝐸ℎ0 𝑢𝑡𝑡 − 𝑢𝑥𝑥 − 2𝑎 − 3 𝑢2 2 2𝜌0 𝑅 4 𝜌0 𝑅 𝐻0 𝑅 𝑢 = 0, 𝑥𝑥 − 2 𝑥𝑥𝑡𝑡 (4) Точное решение в виде бегущей уединенной волны при постоянном значении радиуса R 2 𝑢 x ,t = 6 𝑐1 1 1 2 Sech 𝛽 𝑥 − 𝛽 𝑡 𝑎1 1 − 4𝛽 2 𝑐1 1 − 4𝛽 2 𝑐1 где амплитуда: и скорость: 6𝑐1 𝛽2 Am = , 𝑎1 1 − 4𝑐1 𝛽2 𝑣= 1 , 1 − 4𝛽 2 𝑐1 , (5) (6) (7) Здесь 𝑎1 и 𝑐1 – комбинации коэффициентов уравнения (4), характеризующие упругие свойства стенки, 𝛽 – свободный параметр. Численное исследование эволюции локализованной в волны в аорте В пакете Вольфрам Математика был разработан код, с помощью которого и были решены нелинейные уравнения в частных производных и произведена визуализация полученных решений. Начальное условие (при t=0) представляет собой точное решение уравнения (4): 𝑢 x =6 𝑐1 1 𝛽 2 Sech 𝛽𝑥 2 , 2 𝑎 1 − 4𝛽 𝑐1 (8) Кусочно-непрерывный характер радиуса задается функцией 𝑅 𝑥 : 𝑅 𝑥 = с11 + с21 − с11 𝑇𝑎𝑛ℎ 𝑘𝑚 𝑥 − 𝑥11 − 𝑇𝑎𝑛ℎ 𝑘𝑛 𝑥 − 𝑥12 , (9) гдес11 , с21 – размеры изменения глубины неоднородности,𝑥11 , 𝑥12 – размеры изменения длины неоднородности,𝑘𝑚 ,𝑘𝑛 – крутизна заднего и переднего фронта неоднородности соответственно. Рис. 5. Пример профиля неоднородности при 𝑐11 = 1, 𝑐22 = 0.9, 𝑥11 = 30,𝑥12 = 100,𝑘𝑚 = 4, 𝑘𝑛 = 0.1 Численное исследование эволюции локализованной в волны в аорте (продолжение) Манипулятор Заключение • Получено модельное уравнение для поперечных волн деформации в виде модифицированного уравнения Буссинеска с переменными коэффициентами; • Проведено численное исследование распространения локализованной волны деформации вдоль аорты, разработан код в среде Вольфрам Математика; • Установлены основные качественные и количественные изменения в поведении волны при прохождении неоднородности: образование вторичной и отраженной локализованных волн; • Установлено сходство этих волн с точным решением в виде бегущей уединенной волны; • Это позволяет использовать выражения для параметров аналитического решения для определения параметров неоднородности по измеренным значениям амплитуды и скорости волны; • Возможно дальнейшее использование модели для других частных случаев неоднородности, в частности, расширения стенок аорты; • В перспективе применение модели на практике для диагностики характера и тяжести заболевания (акустодиагностики). Список основной литературы 1. А. Н. Волобуев. Течение жидкости в трубках с эластичными стенками // УФН. – 1995. - Т. 165. - №2. - С. 177 – 186. 2. R. A. Kraenkel, S. Noubissie, P. Woafo. A mathematical model for wave propagation in elastic tubes with inhomogeneities: Application to blood waves propagation // Physica D 236. 2007. 131-140. 3. S. Yomosa. Solitary Waves in Large Blood Vessels // J. Phys. Soc. Japan 56. 1987. 506-520. 4. Википедия – свободная энциклопедия [Электронный ресурс]. http://wikipedia.org . - (дата обращения: 14.11.2013)