Документ 5026235

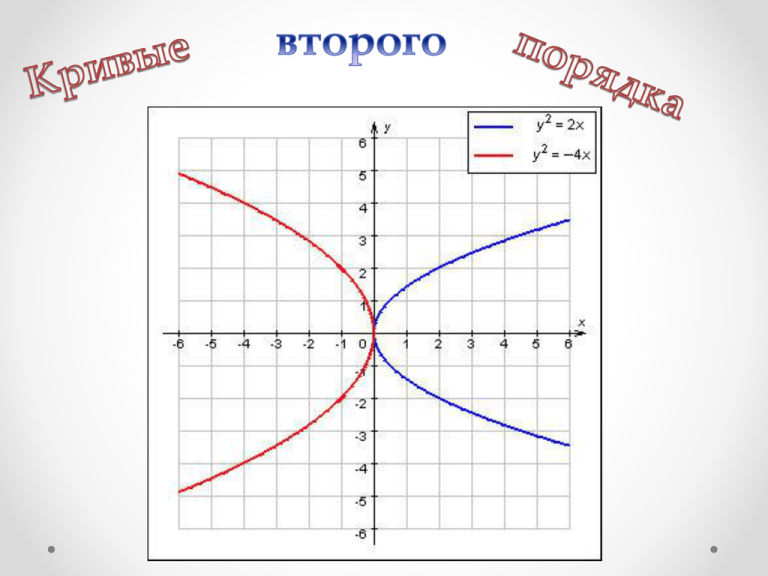
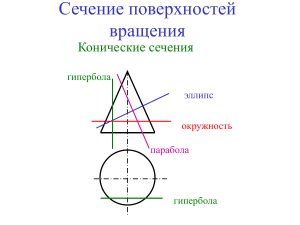
Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой
декартовой системе координат определяется уравнением
Ax 2  2Bxy  Cy 2  2Dx  2Ey  F  0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2+ b2+ c2≠ 0
Кривые второго порядка:
•
•
•
•
Окружность
Эллипс
Гипербола
Парабола
Окружность

AM  R
y
x  a   y  b 
М(x; y)
2
2

R
R
А
0
х

x  a   y  b 
2
2
Каноническое уравнение окружности
Окружностью называется геометрическое место точек на плоскости,
равноудаленных от точки А(a; b) на расстояние R.
 R2
Эллипс
y
r1  r2  2a
M(x; y)
F2
F1
-c
F1(c; 0);
r2
r1
0
c
х
F2 (c; 0)
r1  F1M 
x  c 
r2  F2M 
x  c 
2
2
 y2
 y2
Эллипсом называется геометрическое место точек, сумма расстояний от каждой
из которых до двух точек той же плоскости F1 и F2, называемых фокусами, есть
величина постоянная, равная 2а.
x  c 


x  c 
2
x  c 
2
4a
 a

x  c 
 y2 
2
2
 y 2  2a
2
 y 2    2a 
 
 y 2  4a 2  4a
x  c 
2
x  c 
2
x  c 
2

2
 y 2  

 y 2  x  c   y 2
2
 y 2  4a 2  x 2  2 xc  c 2  x 2  2 xc  c 2
2


2
2

x  c   y   a  xc : 4


 c x  a y  a (a  c )
b2
2
2
a 2 x 2  2a 2 xc  a 2c 2  a 2 y 2  a 4  2a 2 xc  x 2c 2
a
2
2
2

2
2
x2 y 2
 2 1
2
a
b
2
2
2


Каноническое уравнение окружности
Гипербола
Гиперболой называется геометрическое место точек, разность расстояний от
каждой из которых до двух точек той же плоскости F1 и F2, называемых фокусами,
есть величина постоянная, равная 2а.
y
r1  r2  2a
M(x; y)
F1(c; 0);
r1
F2
F1
-c
0
c
r2
х
F2 (c; 0)
r1  F1M 
x  c 
r2  F2M 
x  c 
2
2
 y2
 y2
Гипербола
x  c 
2
 y2 
x  c 
2
 y 2  2a
x  c 
2
 y2 
x  c 
2
 y 2  2a

После тождественных преобразований уравнение примет вид:
b x  a y  a b : (a b
2
2
2
2
2 2
2 2)

x2 y 2
 2 1
2
a
b
Каноническое уравнение гипербола
Гипербола
Парабола
Параболой называется геометрическое место точек на плоскости, для каждой из
p
которых расстояние до некоторой фиксированной точки той же плоскости
, называемой фокусом, равно расстоянию до прямой: x  
y
d
r d
p
F ( ; 0)
2
p0
2
F
p
2
p
2
M(x; y)
r

F ( ;0)
2
0
p
2
х
p

r  FM   x    y 2
2

p
d x
2
Парабола
2
p
p

2
x


y

x



2
2


2
2
p
p
x 2  px 
 y 2  x 2  px 
4
4

y 2  2px
Каноническое уравнение параболы