PPTX 450kb
реклама

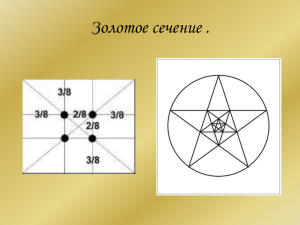
Золотое сечение История • В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника. Арифметические характеристики • Ф=1,618 • Любая степень Фи равна сумме 2 предыдущих степеней. • Ф2=Ф+1 • Золотое сечение — соотношение двух величин, равное соотношению их суммы к большей из данных величин. В процентном округлённом значении — это деление величины на 62 % и 38 %. Геометрические характеристики • Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон. • В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны числу Ф. Золотое сечение в искусстве • Под «правилом золотого сечения» в архитектуре и искусстве обычно понимаются композиции, содержащие пропорции, близкие к золотому сечению. • Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании. • Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий Жолтовский использовал золотое сечение в своих проектах. Ряд Фибоначчи и число Фи • Чи́сла Фибона́ччи — элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи). Связь • • • • • 1/1=1 2/1=2 3/2=1.5 … Fn/Fn-1~~Ф Ссылки • Википедия • Журнал «Мир математики»