2 Средние величины

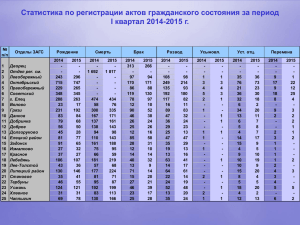
Статистика
Средние величины
Подопригора Игнат Валерьевич,
К.э.н., доцент кафедры экономики
Средние величины
Статистическая совокупность содержит
некоторое количество статистических величин,
имеющих, как правило, разные значения и
признаки, что делает невозможным сравнение
нескольких совокупностей в целом. Для этой
цели применяется
средняя величина как обобщающий показатель
совокупности, характеризующий
уровень изучаемого явления или процесса.
Виды средних величин
1. Средняя арифметическая
– простая
– взвешенная
2.
3.
4.
5.
6.
7.
Средняя гармоническая
Средняя квадратическая
Средняя геометрическая
Средняя хронологическая
Мода (Мо)
Медиана (Ме)
1. Средняя арифметическая простая
X 1  X 2  ...  X N
X 

N
X
N
Средняя арифметическая простая
используется в том случае, если у всех
группировочных признаков равны между
собой частоты признака.
Пример 1
По промышленному предприятию имеются следующие
данные по фактическому и плановому выпуску одного из
изделий в первом полугодии
Выпуск изделий, Январь Февраль Март Апрель Май
шт.
Июнь
По плану
400
420
430
430
440
460
Фактически
380
420
410
400
470
460
Итого
Определить среднемесячные плановый и фактический
выпуск продукции
Пример 1
Выпуск изделий, Январь Февраль Март Апрель Май
шт.
Июнь
Итого
По плану
400
420
430
430
440
460
2 580
Фактически
380
420
410
400
470
460
2 540
Пример 1
Выпуск изделий, Январь Февраль Март Апрель Май
шт.
Июнь
Итого
По плану
400
420
430
430
440
460
2 580
Фактически
380
420
410
400
470
460
2 540
По плану ВП = 2580/6 = 430
Пример 1
Выпуск изделий, Январь Февраль Март Апрель Май
шт.
Июнь
Итого
По плану
400
420
430
430
440
460
2 580
Фактически
380
420
410
400
470
460
2 540
По плану ВП = 2580/6 = 430
Фактически ВП = 2540/6 = 423,3
Пример 2
Вы купили в магазине:
• 2 кг яблок по 80 р/кг
• 3 кг апельсинов по 120 р/кг
• 1 кг бананов по 100 р/кг.
Рассчитайте среднюю цену одного килограмма фруктов
Пример 2
X  (80  120  100) / 3  100
Пример 2
X  (80  120  100) / 3  100
Всего потрачено денег:
(80 * 2  120 * 3  100 *1)  160  360  100  620
Пример 2
X  (80  120  100) / 3  100
Всего потрачено денег:
(80 * 2  120 * 3  100 *1)  160  360  100  620
Всего куплено кг:
2+3+1=6
Пример 2
X  (80  120  100) / 3  100
Всего потрачено денег:
(80 * 2  120 * 3  100 *1)  160  360  100  620
Всего куплено кг:
2+3+1=6
Итого средняя цена 1 кг:
620 / 6 = 103,33 руб.
2. Средняя арифметическая
взвешенная
N
X
Х
i 1
N
f
i 1
f
i i
i
Xi – значение изучаемого
признака
fi – частота изучаемого
признака
Применяется для СГРУППИРОВАННЫХ данных
Пример 2.1
По данным таблицы рассчитать среднюю по трем предприятиям АО
заработную плату.
Предприятие
1
2
3
Численность промышленнопроизводственного персонала
(ППП), чел.
540
275
458
Средняя заработная
плата, руб.
9046
9210
9130
Пример 2.1
По данным таблицы рассчитать среднюю по трем предприятиям АО
заработную плату.
Предприятие
1
2
3
Численность промышленнопроизводственного персонала
(ППП), чел.
540
275
458
Средняя заработная
плата, руб.
9046
9210
9130
9046  540  9210  275  9130  458
xар 
 9111, 65
540  275  458
Пример 2.2
Имеются следующие данные о длине маршрута движения городского
транспорта
Длина маршрута, км
до 8 8-10 10 - 12 12 -14 Свыше 14
Число единиц городского
транспорта, в процентах
к итогу
3,0
12,8
15,2
15,3
38,0
Пример 2.2
Имеются следующие данные о длине маршрута движения городского
транспорта
Длина маршрута, км
до 8 8-10 10 - 12 12 -14 Свыше 14
Число единиц городского
транспорта, в процентах
к итогу
3,0
12,8
15,2
15,3
7 * 3  9 *12  11*15  13 *15  15 * 38
X
3  12  15  15  38
38,0
Пример 2.2
Имеются следующие данные о длине маршрута движения городского
транспорта
Длина маршрута, км
до 8 8-10 10 - 12 12 -14 Свыше 14
Число единиц городского
транспорта, в процентах
к итогу
3,0
12,8
15,2
15,3
38,0
7 * 3  9 *12  11*15  13 *15  15 * 38 1059
X

 12,76
3  12  15  15  38
83
Пример 3
Качество продукции предприятия характеризуется следующими данными
за месяц. Определить средний процент брака в целом по предприятию.
Вид
продукции
А
В
С
Доля брака, %
1,3
0,9
2,4
Стоимость бракованной
продукции, руб.
2135
3560
980
Пример 3
Качество продукции предприятия характеризуется следующими данными
за месяц. Определить средний процент брака в целом по предприятию.
Вид
продукции
А
В
С
Доля брака =
Доля брака, %
1,3
0,9
2,4
Стоимость бракованной
продукции, руб.
2135
3560
980
Стоимость всей бракованной продукции, руб.
Стоимость всей произведенной продукции, руб.
Пример 3
Качество продукции предприятия характеризуется следующими данными
за месяц. Определить средний процент брака в целом по предприятию.
Вид
продукции
А
В
С
Доля брака =
xгар 
Доля брака, %
1,3
0,9
2,4
Стоимость бракованной
продукции, руб.
2135
3560
980
Стоимость всей бракованной продукции, руб.
Стоимость всей произведенной продукции, руб.
2135  3560  980
6675
100 % 
100 %  1,1 %
2135 3560
980
600619, 66


0, 013 0, 009 0, 024
3. Средняя гармоническая
Когда статистическая информация не
содержит частот f по отдельным признакам x
совокупности, а представлена как их
произведение
x f
применяется формула средней
гармонической взвешенной
3. Средняя гармоническая
Средняя арифметическая взвешенная
N
X
x f
i 1
N
i i
f
i 1
i
И обозначим:
x f  w
f  w/ x
3. Средняя гармоническая
взвешенная
n
xгар
w1  w2 

w1 w2


x1 x2
 wn

wn

xn
w
i 1
n
i
wi

i 1 xi
4. Средняя геометрическая
X геом  N X 1  X 2  ...  X N  N
X
Основное применение средняя
геометрическая находит при определении
средних относительных изменений, о чем
сказано в теме «Ряды динамики».
Пример 4
Определить индекс динамики выпуска
продукции
Год
2011
2012
2013
2014
Индекс динамики
1,063
1,097
0,94
1,045
Пример 4
Определить индекс динамики выпуска
продукции
Год
2011
2012
2013
2014
Индекс динамики
1,063
1,097
0,94
1,045
I  1.063 1.097  0.94 1.045  1.035
4
5. Средняя хронологическая
В случае если необходимо посчитать среднее
значение ряда данных, распределенных во
времени используют формулу Средней
хронологической простой, если моменты
времени равноотстоят друг от друга
xn
x1
 x2  ...  xn 1 
2
2
x
n 1
Пример 5
По данным таблицы определить среднегодовую
стоимость основных фондов предприятия (млн.р)
Дата
Стоимость ОФ
01.янв.14
01.апр.14
01.июл.14
135
168
142
01.окт.14 01.янв.15
167
154
Пример 5
По данным таблицы определить среднегодовую
стоимость основных фондов предприятия (млн.р)
Дата
Стоимость ОФ
01.янв.14
01.апр.14
01.июл.14
135
168
142
01.окт.14 01.янв.15
167
154
135
154
 168  142  167 
2  155,357
ОФ  2
4
Мода
Модой называется значение признака,
которое наиболее часто встречается в
совокупности (в статистическом ряду).
Т.е. мода показывает наиболее ТИПИЧНЫЙ
уровень ряда данных.
Пример 6
Имеются данные о тарифном разряде
рабочих: 4, 5, 2, 5, 3, 4, 1, 6 , 5, 4, 3, 3, 6, 5
Определить моду.
Пример 6
Имеются данные о тарифном разряде рабочих:
4, 5, 2, 5, 3, 4, 1, 6, 5, 4, 3, 3, 6, 5, 2
Определить моду.
Количество рабочих 1-го разряда – 1
Количество рабочих 2-го разряда – 2
Количество рабочих 3-го разряда – 3
Количество рабочих 4-го разряда – 3
Количество рабочих 5-го разряда – 4
Количество рабочих 6-го разряда – 2
Медиана
Медианой называется значение признака,
которое расположено в середине
упорядоченного (по возрастанию или
убыванию) ряда и разделяет этот ряд на две
равные по численности части. Если ряд
состоит из четного числа членов, то за
медиану условно принимают среднюю
арифметическую из двух срединных
значений.
Пример 6.1
Имеются данные о тарифном разряде
рабочих: 4, 5, 2, 5, 3, 4, 1, 6 , 5, 4, 3, 3, 6, 5
Определить медиану.
Пример 6.1
Имеются данные о тарифном разряде
рабочих: 4, 5, 2, 5, 3, 4, 1, 6, 5, 4, 3, 3, 6, 5
Определить медиану.
Упорядочиваем ряд данных:
1, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6.
Мода
В интервальных рядах распределения с равными интервалами мода
вычисляется по формуле (модальный интервал определяется по наибольшей
частоте):
M o  xmo  h
xmo
f
f mo  f mo1
mo
 
 f mo1  f mo  f mo1

- нижняя граница модального интервала
h – длина модального интервала
f mo , f mo1 , f mo1 - частоты в модальном, предыдущем и
следующим за модальным интервалах (соответственно)
Пример 7
Распределение строительных организаций области по
стоимости основных фондов (ОФ) представлено в таблице:
Группы предприятий по
стоимости ОФ,
млн руб.
14–16
16–18
18–20
20–22
22–24
Определить моду
Число предприятий
f 
2
6
10
4
3
Пример 7
Распределение строительных организаций области по
стоимости основных фондов (ОФ) представлено в таблице:
Группы предприятий по
стоимости ОФ,
млн руб.
14–16
16–18
18–20
20–22
22–24
Число предприятий
f 
2
6
10
4
3
10  6
M o  18  2
 18,8
(10  6)  (10  4)
Медиана
В интервальных рядах распределения медианное значение
оказывается в каком-то из интервалов признака x. Этот
интервал характерен тем, что его накопленная сумма частот
равна или превышает полусумму всех частот ряда. Значение
медианы вычисляется по формуле
f
M e  xme  h
2
 S me1
f me
Пример 7.1
Распределение строительных организаций области по
стоимости основных фондов (ОФ) представлено в таблице:
Группы предприятий по
стоимости ОФ,
млн руб.
14–16
16–18
18–20
20–22
22–24
Определить медиану
Число предприятий
f 
2
6
10
4
3
S m 
Пример 7.1
Распределение строительных организаций области по
стоимости основных фондов (ОФ) представлено в таблице:
Группы предприятий по
стоимости ОФ,
млн руб.
14–16
16–18
18–20
20–22
22–24
Число предприятий
f 
2
6
10
4
3
12,5  8
M e  18  2
 18,9
10
Накопленная
частота
S m 
2
8
18
–
–
Пример 8
Определить среднюю, медианную и модальную
заработную плату сотрудников предприятия:
Численность
сотрудников
(чел)
100
1
Заработная
плата
(т.р.)
10
1000
Пример 8
Определить среднюю, медианную и модальную
заработную плату сотрудников предприятия:
Численность
сотрудников
(чел)
100
1
Ср. з/п = 20 т.р.
Мода = Медиана = 10 т.р.
Заработная
плата
(т.р.)
10
1000
Спасибо за внимание