Начала математического анализа. По материалам открытого
реклама

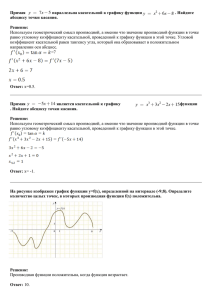
МБОУ СОШ №7 г. Шахты Ростовской области Начала математического анализа по материалам открытого банка заданий ЕГЭ ФИПИ Автор: учитель математики Скокова Татьяна Борисовна Найдите наименьшее значение функции y=x3+6x2+9x+21 на отрезке [−3; 0]. Решение. 1. Найдем производную данной функции y'=3x2+12x+9; 2. Найдём стационарные и критические точки, расположенные внутри отрезка: для этого решим y'= 0, т.е уравнение 3x2+12x+9 = 0, получим х1= -3; х2=-1; 3. Вычислим значения функции в данных точках, вычислить значения функции на концах отрезка у(-3)=(-3)3+6(-3)2+9(-3)+21=- 27+54-27+21=21, у(-1)=(-1)3+6(-1)2+9(-1)+21= -1+6-9+21= 17, у(0)=(0)3+6(0)2+9(0)+21= 21; 4. Из полученных значений выбрать наименьшее значение. Ответ: 17. Найдите наименьшее значение функции Решение. 1. Найдем производную данной функции y'= 2. Найдём стационарные и критические точки, расположенные внутри отрезка . Для этого решим y'= 0, т.е уравнение , получим х = . 3. Вычислим значения функции в данной точке, вычислить значения функции на концах отрезка у( )= у( )= у(0)= 4. Из полученных значений выбрать наименьшее значение. Ответ: -2 Найдите наибольшее значение функции y = 15x−3sinx+5 на отрезке [− ;0]. Решение. 1. Найдем производную данной функции y'= 15−3cosx . 2. Найдём стационарные и критические точки, расположенные внутри отрезка [− ;0]. Для этого решим y'= 0, т.е уравнение 15 −3cosx =0, 3cosx =15, cosx=5 – нет решений т.к. -1 ≤ cosx ≤ 1. 3. Вычислим значения функции на концах отрезка у( - )= y = 15(- ) −3sin(- )+5 ≈ -15,55 у(0)= 15.0−3sin0+5=5 4. Из полученных значений выбрать наименьшее значение. Ответ: 5 Найдите точку максимума функции y=(x−2)2(x−4)+5. Решение. 1. Упростим выражение (x−2)2(x−4)+5 =х3-8х2+20х-11; 2. Найдем производную данной функции y'=3x2-16x+20; 2. Решим y'= 0, т.е уравнение 3x2-16x+20 = 0, получим х1= 2; х2= ; 3. Полученные точки разбивают числовую ось на интервалы: Если производная меняет свой знак с "+" на "-", т.е. функция меняет возрастание на убывание в некоторой точке, то такая точка и есть точка максимума функции. Если производная меняет свой знак с «-" на «+", т.е. функция меняет убывание на возрастание в некоторой точке, то такая точка и есть точка минимума функции. На интервале (–∞;2) функция возрастает, на интервале (2; ) функция убывает. Значит х = 2 это точка максимума. Ответ: 2 Найдите наибольшее значение функции Решение. При решении некоторых заданий на нахождение наибольшего и наименьшего значений функции (особенно сложных) можно обойтись и без производной. Сложную функцию u(v(x)) можно представить в виде цепочки простых функций: v(x)промежуточный аргумент, x – независимая переменная. Вид исходной функции: u(v(x))= -функция монотонно возрастающая на всей области определения (D(u): 5-4x -x2 ≥0, значит наибольшее значение она будет иметь тогда, когда наибольшее значение будет иметь функция промежуточного аргумента v(x)= 5-4x - x2 . v(x)= 5-4x -x2 – квадратичная функция, графиком которой является парабола ветвями вниз, т.к. старший коэффициент -1<0. Следовательно, наибольшее значение квадратичная функция будет иметь при вершине параболы. x0=-b/2a, x0=4/-2, x0=-2 принадлежит D(u). Следовательно, исходная функция наибольшее значение, тоже, будет иметь при x0=-2 . Вычислим его: . Ответ: 3 Найдите точку максимума функции y=log2(2+2x−x2)−2 Решение: Исходную функцию можно представить в виде u(v(x)) =log2v(x)−2, v(x)= 2+2x−x2 (свободный член −2, при определении точек экстремума не играет никакой роли). D(u): (2+2x−x2)−2≥0. Логарифмическая функция с основанием 2 монотонно возрастающая на всей области определения, поэтому точка максимума функции v(x)= 2+2x−x2 автоматически будет являться точкой максимума функции u(v(x)) =log2v(x)−2. v(x)= 2+2x−x2 - квадратичная функция, графиком которой является парабола ветвями вниз, т.к. старший коэффициент -1<0. Следовательно, наибольшее значение квадратичная функция будет иметь при вершине параболы. x0=-b/2a, x0=-2/-2, x0=1 - принадлежит D(u). То есть x0=1-точка максимума функции v(x)= 2+2x−x2, а значит, и функции y=log2(2+2x−x2)−2. Ответ: 1 На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0 Решение. 1 способ. f ′(хo) = k. Воспользуемся формулой (y2-y1)= k(x2-x1) где k –угловой коэффициент касательной к графику функции в точке x0 , отсюда k = (y2- y1) / (х2 -х1). Для этого на касательной найдем две точки с целыми значениями, в нашем случае это А(0;-2) и В(5;8), подставим их значения в формулу и вычислим. k = (-2-8) / (0 -5)= -10/-5=2. Ответ: 2 На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Решение. 2 способ Значение производной функции f ′(хo) = tg α = k равно угловому коэффициенту касательной, проведенной к графику этой функции в данной точке. В нашем случае k < 0, так как α – тупой угол (tg α < 0). Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа. Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC. tg(180°− α) = ВС : АС = 1 : 5 = 0,2, тогда tg α = − tg (180°− α) = −0,2 Ответ: -0,2 На рисунке изображен график функции f(x), определенной на интервале (−5;5). Найдите количество точек, в которых производная функции f(x) равна 0. Решение. Если производная функции равна нулю, то угловой коэффициент касательной, проведённой к графику функции в этой точке (или тангенс угла наклона касательной к положительному направлению оси ОХ) тоже равен нулю. Иначе говоря, касательная к графику функции в этой точке параллельна оси ОХ. Осталось посчитать, сколько горизонтальных касательных можно провести. Ответ: 4 На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=5. Решение. Если касательная к графику функции f(x) параллельна прямой у = 5 или совпадает с ней, то ее угловой коэффициент k = 0, а значит нам нужно найти количество точек, в которых производная функции f ′(x) = 0. Для этого на графике производной проведем прямую у = 0 (она совпадает с осью Ох) и посчитаем количество точек графика производной, лежащих на этой линии. Таких точек 4. Ответ: 4 На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−6;6). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=−3x−11 или совпадает с ней. Решение. Если касательная к графику функции f(x) параллельна прямой у = -3х - 11 или совпадает с ней, то ее угловой коэффициент k = -3, а значит нам нужно найти количество точек, в которых производная функции f ′(x) = -3. Для этого на графике производной проведем прямую у = -3 и посчитаем количество точек графика производной, лежащих на этой линии. Таких точек 4. Ответ: 4 На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−8;3). В какой точке отрезка [−3;2] функция f(x) принимает наибольшее значение? Решение. На отрезке [–3; 2] производная функции отрицательна, значит, сама функция убывает, а значит, наименьшее значение на этом отрезке она принимает на правом конце отрезка, то есть в точке 2. Ответ: 2 На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Определите количество целых точек, в которых производная функции положительна. Решение. Производная функции положительна, если сама функция f(x) возрастает, а значит, необходимо найти количество целых точек, входящих в промежутки возрастания функции. Таких точек 4. x1=-2; x2=-1; x3=5; x4=6. Ответ: 6 На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−7;14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−6;9]. Решение. Если производная на интервале положительна, то функция на этом интервале возрастает. Если производная отрицательна, то функция убывает. Если производная меняет свой знак с "+" на "-", т.е. функция меняет возрастание на убывание в некоторой точке, то такая точка и есть точка максимума функции. В нашем случае это точка х=7 и она единственная. Ответ: 1 На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−11;11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−10;10]. Решение. Если производная на интервале положительна, то функция на этом интервале возрастает, если производная отрицательна, то функция убывает. Точка экстремума - это точка, в которой достигается максимальное или минимальное значение функции. Если производная меняет свой знак с "+" на "-", т.е. функция меняет возрастание на убывание в некоторой точке, то такая точка и есть точка максимума функции. Если производная меняет свой знак с «-" на «+", т.е. функция меняет убывание на возрастание в некоторой точке, то такая точка и есть точка минимума функции. В нашем случае таких точек 5. Ответ: 5 На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−5;7). В ответе укажите сумму целых точек, входящих в эти промежутки. Решение. Если производная отрицательна, то функция убывает. Осталось найти сумму целых точек, входящих в этот промежуток: -2+(-1)+0+1+2+3+4+5+6 = 18. Ответ: 18 На рисунке изображён график y=f′(x) — производной функции f(x). На оси абсцисс отмечено восемь точек: x1, x2, x3, …, x8. Сколько из этих точек лежит на промежутках возрастания функции f(x)? Решение. Если производная на интервале положительна, то функция на этом интервале возрастает. Очевидно, что на промежутке возрастания функции лежит 3 точки. Ответ: 3 На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−11;3). В ответе укажите длину наибольшего из них. Решение. На промежутках (-10;-6) и (-2;2) производная функции отрицательна, значит на этих промежутках функция убывает. Найдем длины этих промежутков: Длины промежутков убывания функции одинаковые. Ответ: 4 На рисунке изображен график функции y=f(x) и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку. Решение. f ′(хo) = tg α = k. В точках –1 и 1 производная имеет отрицательное значение, в точках –2 и 2 она имеет положительное значение. Следовательно в данном случае необходимо проанализировать точки –2 и 2 и определить в какой из них значении будет наибольшим. Построим касательные проходящие через указанные точки (см. рис. выше). При изменении угла наклона прямой от 0о до 90о значение тангенса, а значит и производной, изменяется соответственно от 0 до +∞; Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке –2 будет наибольшим. Ответ: -2 Прямая у = 4х + 11 параллельна касательной к графику функции у = х2 + 8х + 6. Найдите абсциссу точки касания. Решение: Если прямая параллельна касательной к графику функции в какой-то точке (назовем ее хо), то ее угловой коэффициент равен значению производной функции в точке хо. В нашем случае угловой коэффициент касательной к графику функции k = 4, т.к. из уравнения у = 4х +11 k = f ′(xo) = 4 Производная функции f ′(x) = (х2 + 8х + 6)′ = 2x + 8. Значит, для нахождения искомой точки касания необходимо, чтобы 2хo + 8 = 4, откуда хо = – 2. Ответ: -2 Прямая y=−5x+8 является касательной к графику функции 28x2+bx+15. Найдите b, учитывая, что абсцисса точки касания больше 0. Решение. Производная функции в точке касания совпадает с угловым коэффициентом прямой, т.е. у1' = y2‘, получим -5 = 56х + b, отсюда b=-5 -56х . Подставим полученное выражение в исходное значение функции и упростим: 28x2+(-5-56x)x+15= -28x2+7. Точка касания принадлежит и прямой и параболе, т.е. у1 = у2, поэтому -28x2+7 = −5x+8. Решив полученное уравнение имеем х1 = –0,5 – не удовлетворяет условию задачи, т.к. абсцисса точки касания больше 0; х2 = 0,5. Подставим х2 = 0,5 в b=-5 -56х, получим b=-33. Ответ: -33 Материальная точка движется прямолинейно по закону x(t)=6t2−48t+17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9 с. Решение. Физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого-либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество). Найдем закон изменения скорости: v (t) = x′(t) = 12t – 48 м/с. При t = 9 имеем: v (9) = 12.9 – 48 = 60 м/с. Ответ: 60 На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x3+30x2+302x−158 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Решение. Интеграл это есть площадь фигуры ограниченной графиком функции f (x), прямыми х = а и х = b и осью Оx. Теорема (Ньютона–Лейбница): Таким образом, задача сводится к вычислению определённого интеграла данной функции на интервале от –11 до –9, или другими словами нам необходимо найти разность значений первообразных вычисленных в указанных точках: F(-9)= (-9)3+30(-9)2+302(-9)−158 = -279+2430-2718-158= -725; F(-11)= (-11)3+30(-11)2+302(-11)−158 = - 1331+3630-3322-158=-1181; F(-9)-F(-11) = -725- (-1181)=456. Ответ: 456 На рисунке изображён график функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)−F(2), где F(x) — одна из первообразных функции f(x). Решение. Интеграл это есть площадь фигуры ограниченной графиком функции f (x), прямыми х = а и х = b и осью Оx. Теорема (Ньютона–Лейбница): Таким образом, задача сводится к нахождению площади трапеции (интервал от 2 до 8). Но её можно вычислить по клеткам. Ответ: 7 На рисунке изображён график функции y = F (x) — одной из первообразных некоторой функции f (x), определённой на интервале (–3;5). Пользуясь рисунком, определите количество решений уравнения f (x) = 0 на отрезке [–2;4]. Решение. Нам нужно определить сколько имеется точек на данном графике, в которых F′(x) = 0. Мы знаем, что производная равна 0 в тех точках, где касательная к графику функции параллельна оси ох. На интервале [–2;4]таких точек 10. Ответ: 10 Используемые материалы 1. http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege; 2. http://matematikalegko.ru/proizvodnaya-pervoobraznaya/zadachina-pervoobraznuyu.html; 3. http://matematikalegko.ru/?s=задачи+на+производную.