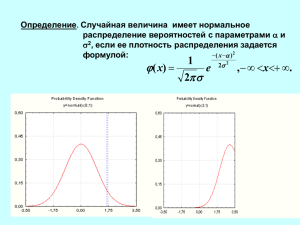
метод наименьших квадратов. Одномерная линейная регрессия
реклама
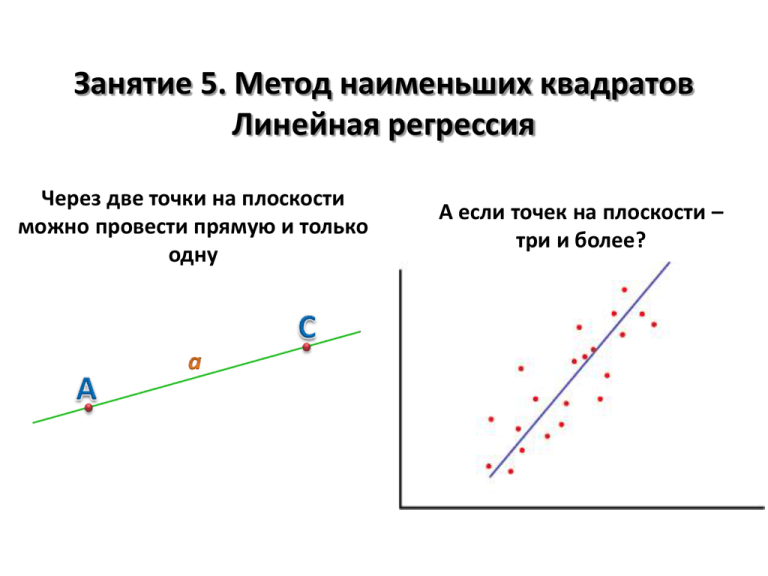
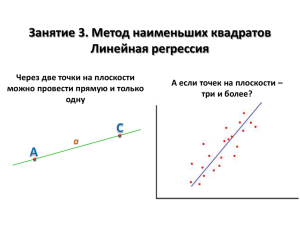
Занятие 5. Метод наименьших квадратов Линейная регрессия Через две точки на плоскости можно провести прямую и только одну А если точек на плоскости – три и более? Метод наименьших квадратов Дано: 1. Набор экспериментальных точек (𝒚𝟏 , 𝒙𝟏 ), (𝒚𝟐 , 𝒙𝟐 ), …, (𝒚𝒏 , 𝒙𝒏 ) 2. Линейная модель 𝒚 = 𝒂 + 𝒃𝒙 Найти коэффициенты 𝒂 и 𝒃 Переопределённая система уравнений 𝑎 + 𝑏𝑥1 = 𝑦1 𝑎 + 𝑏𝑥2 = 𝑦2 … 𝑎 + 𝑏𝑥𝑛 = 𝑦𝑛 В общем случае решения не имеет (т.к. экспериментальные точки обычно не ложатся в точности на одну прямую) Необходимость в приближенных методах Метод наименьших квадратов (МНК) Минимизация суммы квадратов отклонений RSS (Resudiual Sum of Squares) 𝑅𝑆𝑆 = 𝑦𝑖 − (𝑎 + 𝑏𝑥𝑖 ) 𝑖 2 Линейная регрессия: коэффициенты Минимизируемая функция 𝑅𝑆𝑆 = 𝑦𝑖 − (𝑎 + 𝑏𝑥𝑖 ) Результат расчёта 2 𝑎 = 𝑦 − 𝑏𝑥 𝑥𝑦 − 𝑥 𝑦 𝑏= 2 𝑥 − 𝑥 2 𝑖 Поиск стационарных точек для RSS 𝜕𝑅𝑆𝑆 = 𝜕𝑎 𝜕𝑅𝑆𝑆 = 𝜕𝑏 𝑦𝑖 − 𝑛𝑎 − 𝑏 2 𝑦𝑖 − 𝑎 − 𝑏𝑥𝑖 = 0 𝑖 𝑖 𝑖 𝑦 − 𝑎 − 𝑏𝑥 = 0 𝑥𝑦 − 𝑎𝑥 − 𝑏𝑥 2 = 0 𝑖 𝑥𝑖 𝑦𝑖 − 𝑎 2 𝑦𝑖 − 𝑎 − 𝑏𝑥𝑖 𝑥𝑖 = 0 𝑖 𝑥𝑖 = 0 𝑥𝑖2 = 0 𝑥𝑖 − 𝑏 𝑖 𝑖 𝑎 = 𝑦 − 𝑏𝑥 𝑎 = 𝑦 − 𝑏𝑥 2 𝑥𝑦 − (𝑦 − 𝑏𝑥)𝑥 − 𝑏𝑥 2 = 0 𝑥𝑦 − 𝑥 𝑦 + 𝑏 𝑥 − 𝑥 2 = 0 Линейная регрессия: коэффициенты r и R2 𝑅𝑆𝑆 = Коэффициент детерминации R2 𝑅2 = 1 − 𝑖 𝑖 𝑦𝑖 − 𝑦𝑖 𝑦𝑖 − 𝑦 2 2 =1− 2 𝑦𝑖 − 𝑦𝑖 𝑖 𝑅𝑆𝑆 𝐸𝑆𝑆 = 𝑇𝑆𝑆 𝑇𝑆𝑆 residual sum of squares (сумма квадратов отклонений) 𝑅𝑆𝑆 + 𝐸𝑆𝑆 = 𝑇𝑆𝑆 𝑇𝑆𝑆 = 𝑦𝑖 − 𝑦 2 𝑖 total sum of squares (общая сумма квадратов) Коэффициент корреляции Пирсона 𝒓𝒚,𝒚 𝑟𝑦,𝑦 = 𝑖 (𝑦𝑖 − 𝑦)(𝑦 − 𝑦) 𝑖 (𝑦𝑖 −𝑦)2 𝑖 (𝑦𝑖 − 𝑦)2 = 𝑇𝑆𝑆 ⋅ 𝐸𝑆𝑆 𝑦𝑖 = 𝑎 + 𝑏𝑥𝑖 Связь между R2 и 𝒓𝒚,𝒚 𝑟𝑦,𝑦 = 𝑖 (𝑦𝑖 − 𝑦𝑖 + 𝑦𝑖 − 𝑦)(𝑦𝑖 − 𝑦) 𝑇𝑆𝑆 ⋅ 𝐸𝑆𝑆 𝐸𝑆𝑆 = 𝑖 (𝑦𝑖 − 𝑦)(𝑦𝑖 − 𝑦) 𝑦𝑖 − 𝑦 2 𝑖 explained sum of squares (объяснённая сумма квадратов) 0 (т.к. МНК) = 𝑖 (𝑦𝑖 − 𝑦𝑖 )(𝑦𝑖 − 𝑦) + 𝑇𝑆𝑆 ⋅ 𝐸𝑆𝑆 𝑖 𝑦𝑖 − 𝑦 2 = 𝐸𝑆𝑆 = 𝑇𝑆𝑆 𝑅2 Линейная регрессия: критерий Фишера (F-тест) Шаг 1. Найти Fэмп 𝐹𝑒𝑚𝑝 𝑅2 𝑓2 = ⋅ 1 − 𝑅2 𝑓1 𝑓2 - число степеней свободы для данных (N – 2 для 𝑦 = 𝑎 + 𝑏𝑥) 𝑓1 - число независимых коэффициентов (1 для 𝑦 = 𝑎 + 𝑏𝑥) Откуда взята формула? 𝐸𝑆𝑆/𝑓1 𝐸𝑆𝑆/𝑇𝑆𝑆 𝑓2 𝑅2 𝑓2 = ⋅ = ⋅ 𝑅𝑆𝑆/𝑓2 𝑅𝑆𝑆/𝑇𝑆𝑆 𝑓1 1 − 𝑅2 𝑓1 Шаг 2. Сравнить с табличным значением квантиля Если 𝐹𝑒𝑚𝑝 ~𝐹 𝑓1 ; 𝑓2 , то зависимость статистически незначима На практике: Если 𝐹𝑒𝑚𝑝 < 𝐹 𝛼; 𝑓1 ; 𝑓2 (т.е. сравнивают с табличным значением квантиля) Пример: R2=0.667, N=11, аппроксимация y = a + bx 𝐹𝑒𝑚𝑝 = 0.667 9 ⋅ = 18 0.333 1 𝐹 0.95,1,9 = 5.12 Регрессия значима Квартет Энскомба (Anscombe’s quartet) y=3.00+0.500x r=0.816 y=3.00+0.500x r=0.816 y=3.00+0.500x r=0.816 y=3.00+0.500x r=0.816 Линейная регрессия: доверительные интервалы 𝑦 = 𝑎 + 𝑏𝑥 𝑠𝑒2 = 𝑖 𝑦𝑖 − 𝑦𝑖 𝑁−2 2 = 𝑅𝑆𝑆 𝑁−2 Доверительные интервалы коэффициентов регрессии 𝑠𝑎2 𝑠𝑏2 = 1 + 𝑛 𝑠𝑒2 = 𝑖 𝑖 𝑠𝑒2 𝑥𝑖 − 𝑥 𝑥 2 𝑥𝑖 − 𝑥 Δ𝑎 = 𝑠𝑎 ⋅ 𝑡(𝛼; 𝑁 − 2) 2 Δ𝑏 = 𝑠𝑏 ⋅ 𝑡(𝛼; 𝑁 − 2) 2 Доверительные интервалы предсказанных значений 2 𝑠𝑦2𝑗 = 𝑠𝑒2 𝑥𝑗 − 𝑥 1 + 𝑛 𝑖 𝑥𝑖 − 𝑥 2 Δ𝑦𝑖 = 𝑠𝑦𝑖 ⋅ 𝑡(𝛼; 𝑁 − 2) Линейная регрессия в MS Excel Способ 1. Линия тренда на графике 1. Построить точечный график по имеющимся данным вида (yi, xi) 2. Щелкнуть правой кнопкой мыши на серии точек и выбрать «добавить линию тренда» 3. Отметить флажками нужные опции (вид аппроксимирующей функции, показывать ли уравнение на диаграмме, показывать ли R2 и т.п.) Нагляден, но не проводятся F-тест и оценка доверительных интервалов коэффициентов регрессии Способ 2. Использование пакета анализа данных 1. Выбрать вкладку данные, щелкнуть по пункту меню «анализ данных» 2. Из предлагаемых опций выбрать регрессию 3. Указать входные данные и изучить результат Нагляден, содержит F-тест и оценку доверительных интервалов коэффициентов регрессии Способ 3. Вручную Использовать функции MS Excel вроде КОВАР, ДИСП, СРЗНАЧ, СУММ, КОРРЕЛ и т.п. На практике способ не удобен, но полезен для понимания сути происходящего Линейная регрессия: линеаризация Если данные описываются нелинейной зависимостью, то в некоторых случаях её можно линеаризовать 𝐸𝑎 (уравнение Аррениуса) 𝑅𝑇 𝐸𝑎 (т.е. вместо (k; T) – (ln k; 1/T) 𝑅𝑇 Пример 1: 𝑘1 = 𝑘0 𝑒𝑥𝑝 − Решение: ln 𝑘1 = ln 𝑘0 − ) Пример 2: Δ𝑚𝑖𝑥 𝐻 = 𝑥(1 − 𝑥)(𝐴 + 𝐵𝑥) (энтальпия смешения) Δ 𝐻 Решение: 𝑚𝑖𝑥 = 𝐴 + 𝐵𝑥 𝑥(1−𝑥) 𝑣𝑚 𝑆 (схема 𝑆+𝐾𝑚 1 𝐾 + 𝑚 𝑣𝑚 𝑣𝑚 𝑆 Пример 3: 𝑣 = 1 𝑣 Решение: = Михаэлиса-Ментен)