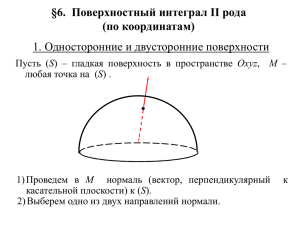
к теме 12
реклама
Тройной интеграл
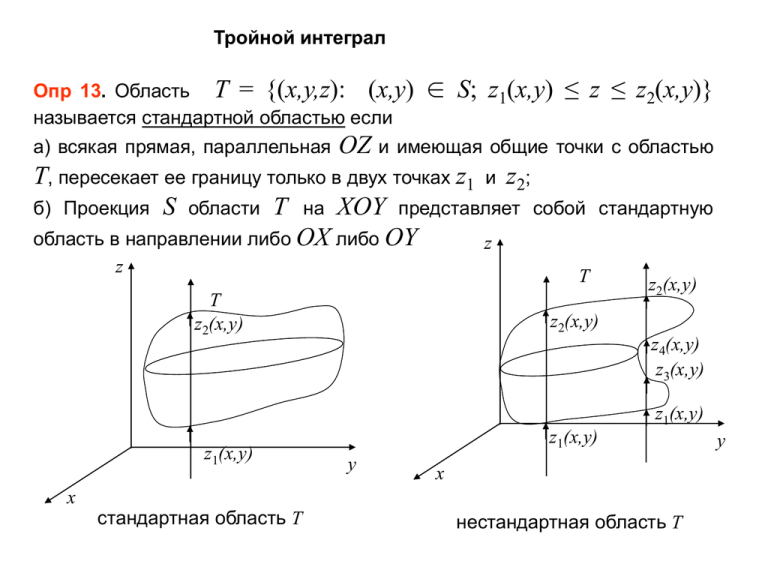
Опр 13. Область T = {(x,y,z): (x,y)
называется стандартной областью если
∈ S; z1(x,y) ≤ z ≤ z2(x,y)}
OZ и имеющая общие точки с областью
Т, пересекает ее границу только в двух точках z1 и z2;
б) Проекция S области Т на XOY представляет собой стандартную
область в направлении либо OX либо OY
z
а) всякая прямая, параллельная
z
T
T
z2(x,y)
z2(x,y)
z2(x,y)
z4(x,y)
z3(x,y)
z1(x,y)
z1(x,y)
x
стандартная область Т
z1(x,y)
y
x
нестандартная область Т
y
Теорема 27 (о вычислении тройного интеграла).
Пусть выполняется 3 условия:
1) область G – стандартная
2)
∃
f ( x, y, z )dG
G
3) ∀ x,y ∈ S ∃ J ( x, y )
z ( x, y )
2
f ( x, y, z)dz
z ( x, y )
1
Тогда
∃ определенный интеграл
J ( x, y)dxdy
S
и справедливо равенство
z2 ( x , y )
J
(
x
,
y
)
dxdy
f
(
x
,
y
,
z
)
dz
S
S z (x, y )
dxdy
1
записывают
b
y ( x)
2
z2 ( x , y )
a
y ( x)
1
z1 ( x , y )
f ( x, y, z)dxdydz dx dy f ( x, y, z)dz
G
Если T стандартная в любом направлении, то пределы интегрирования
можно расставить любыми из 6-и способов
f ( x, y, z)dxdydz
dx dy f ( x, y, z )dz
G
b
y ( x)
2
z2 ( x , y )
a
y ( x)
1
z1 ( x , y )
d
x ( y)
2
z2 ( x , y )
dy
dx f ( x, y, z)dz
c
x ( y)
1
z1 ( x , y )
b
z ( x)
2
y2 ( x , z )
dx dz
f ( x, y, z)dy
a
z ( x)
1
y1 ( x , z )
q
y (z)
2
x2 ( y , z )
dz
p
dy f ( x, y, z)dx
y (z)
1
x1 ( y , z )
проекция T на XOY
проекция T на XOY
проекция T на XOZ
проекция T на YOZ
Физические и геометрические приложения
двойного и тройного интеграла
Двойной интеграл
Площадь плоской области S
S ds dxdy
S
Объем цилиндрического бруса
S
V f ( x, y )ds
S
Масса неоднородной пластины с
переменной плотностью (x,y)
Статический момент пластины S
относительно оси OY
Статический момент пластины S
относительно оси OX
M ( x, y )ds
S
M y x ( x, y )dxdy
S
M x y ( x, y )dxdy
S
Центр тяжести неоднородной
пластины S
x ( x, y)dxdy
( x, y)dxdy
My
xc
M
S
S
yc
Mx
M
y ( x, y)dxdy
( x, y)dxdy
S
S
Момент инерции пластины S
относительно центра O
Момент инерции пластины S
относительно оси OX и OY
I O ( x 2 y 2 ) ( x, y )dxdy
S
I x y 2 ( x, y )dxdy
S
I y x 2 ( x, y )dxdy
S
Тройной интеграл
Объем тела V
V dv dxdydz
V
Масса неоднородной объемной
области V с переменной
плотностью (x,y,z)
V
M ( x, y, z )dxdydz
V
Статический момент
относительно плоскости ZOY
M yz x ( x, y, z )dxdydz
Статический момент
относительно плоскости ZOX
M xz y ( x, y, z )dxdydz
V
V
Статический момент
относительно плоскости YOX
M xy z ( x, y, z )dxdydz
V
Координаты центра тяжести
неоднородного тела V
M yz
xc
M
yc
M xz
M
M xy
zc
M
Момент инерции относительно
оси OX
I x ( y 2 z 2 ) ( x, y, z )dxdydz
Момент инерции относительно
оси OY
I y ( x 2 z 2 ) ( x, y, z )dxdydz
Момент инерции относительно
оси OZ
V
V
I z ( x 2 y 2 ) ( x, y, z )dxdydz
V
Момент инерции относительно
центра O
I O ( x 2 y 2 z 2 ) ( x, y )dxdy
S
Многомерный интеграл
Пусть функция U
области
= f(x1, x2, …,xn)
определена в n - мерной
G ∈ Rn.
Интеграл от функции U = f(x1, x2, …,xn) вводится как предел
соответствующей интегральной суммы и обозначается
I ... f ( x1 , x2 ,..., xn )dx1dx2 ...dxn
n раз
Вычисление сводится к последовательному нахождению интегралов
.
b
I dx1
a
x 2 ( x1 )
x3 ( x1 , x2 )
dy
x 2 ( x1 )
x3 ( x1 , x2 )
x n ( x1 , x2 ,..., xn )
...
f ( x , x ,..., x )dx
x n ( x1 , x2 ,..., xn )
1
2
n
n
Терминология
Тройной интеграл
Неоднородная пластина
Статический момент
Момент инерции
Центр тяжести
Многомерный интеграл
Понимать! Уметь произносить! Запомнить! Использовать!