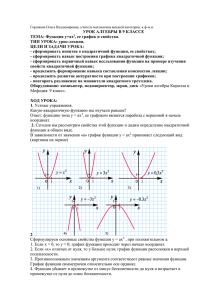
ФУНКЦИЯ у=ах2+вх+с, ее свойства

ФУНКЦИЯ у=ах2+вх+с,
ее свойства и
40 работа:
Устная
• Назовите коэффициент: у 20
= 4 х2; у = - 5 х2 ; у = 1/2 х2;
у = - 1/3 х2
0
• Найдите координаты вершины графика функции у = 7 х2
-8
-6
-4
-2
0
2
4
6
8
• Назовите промежутки возрастания
и убывания функции
-20
у = - 3 х2
-40
• Найдите область определения
функции у = 0,5 х2
2
• Найдите множество значений
функции
у
=
14
х
-60
• Назовите точки разрыва функции у = 11 х2
-80 выполнить, чтобы из
• Какое действие необходимо
графика функции у = х2 получить график функции:
-100
2
2
у = 4 х ; у = - 5 х ; у = 1/2 х2 ; у = - 1/3 х2
• Прочитайте график функции:
Цель занятия:
Научиться строить график квадратичной функции
у = ах2 + вх + с и описывать ее свойства
у
2
1
у2
у1
х
Рассмотрим многочлен ах2+вх+с, где а, в, с – числа
(коэффициенты), причем а  0.
ах2+вх+с – квадратный трехчлен
ах2 - старший член квадратного трехчлена
а – старший коэффициент
у= ах2+вх+с – квадратичная функция, а  0
Графиком квадратичной функции у= ах2+вх+с является
парабола, которая получается из параболы у= ах2
параллельным переносом.
ó  2( õ  2)  20
ó  2 õ2  20
2
80
70
ó  2õ
2
60
50
ó  2( õ  4) 2
40
30
20
10
0
-8
-6
-4
-2
0
2
4
6
8
Алгоритм построения графика квадратичной
функции
• Определить направление «ветвей» параболы.
â
â
• Найти координаты вершины параболы (  2à ; f ( 2à ) ).
• Построить на координатной плоскости данную точку, провести ось
параболы.
• На оси х взять две точки, симметричные относительно оси параболы
(одну х=0).
• Найти значения функции в данных точках, отметить их на
координатной плоскости.
• Через полученные три точки построить параболу.
• При необходимости взять еще две точки, симметричные оси.
Построим график функции у = х2 - 4х + 2
Построение
• Ветви параболы направлены вверх (а=1, 1>0)
• Координаты вершины: х = 4/2*1 = 2,
у = f(2) = 22 – 4*2 +2= -2.
В системе координат отметим точку (2; -2).
• Ось симметрии прямая х = 2.
• Найдем координаты двух точек (0; 2) и (4; 2).
• Отметим полученные точки в системе координат.
• Построим параболу по данным точкам.
у
у = х2 - 4х + 2
2
1
-1
-2
1
2
4
х
Постройте графики функций
в одной системе координат:
1.
1 2

У = 18 õ  12
Х € [- 12; 12]
ПРОВЕРЯЕМ?
2.
1 2

У = 8 õ 6
Х € [- 4; 4]
ПРОВЕРЯЕМ?
3.
У= 
1
 õ  82  6
8
Х € [- 12; -4]
ПРОВЕРЯЕМ?
4.
У
=
1
 õ  82  6
8
Х € [4 ; 12]
ПРОВЕРЯЕМ?
5.
У = 2 (х + 3) 2 - 9
Х € [- 4; -0,3]
ПРОВЕРЯЕМ?
6.
У = 1,5 (х + 3) 2 - 10
Х € [- 4; 0,2]
ПРОВЕРЯЕМ?
График 1 функции
14
12
10
8
6
4
2
0
-15
-10
-5
0
5
10
15
График 2 функции
14
12
10
8
6
4
2
0
-15
-10
-5
0
5
10
15
График 3 функции
14
12
10
8
6
4
2
0
-15
-10
-5
-2
-4
0
5
10
15
График 4 функции
14
12
10
8
6
4
2
0
-15
-10
-5
-2
-4
0
5
10
15
График 5 функции
15
10
5
0
-15
-10
-5
0
-5
-10
-15
5
10
15
График 6 функции
15
10
5
0
-15
-10
-5
0
-5
-10
-15
5
10
15
Прочитайте график функции
(перечислите свойства функции по ее графику).
у
у = х2 - 4х + 2
2
1
1
-2
2
4
х
Домашнее задание
•
•
•
•
§ 13
1 уровень: № 466 а, № 467 а
2 уровень: № 468 а, б
3 уровень: № 475, 487
• Творческое задание: выполнить рисунок графиками
квадратичной функции.
Спасибо за работу!
Кучева Ирина Ивановна,
учитель математики
МОУ «Верхказанская СОШ»
С. Верх-Казанка
Большемуртинского района
Красноярского края
vkazanka_scool@mail.ru