Презентация по дисциплине
реклама
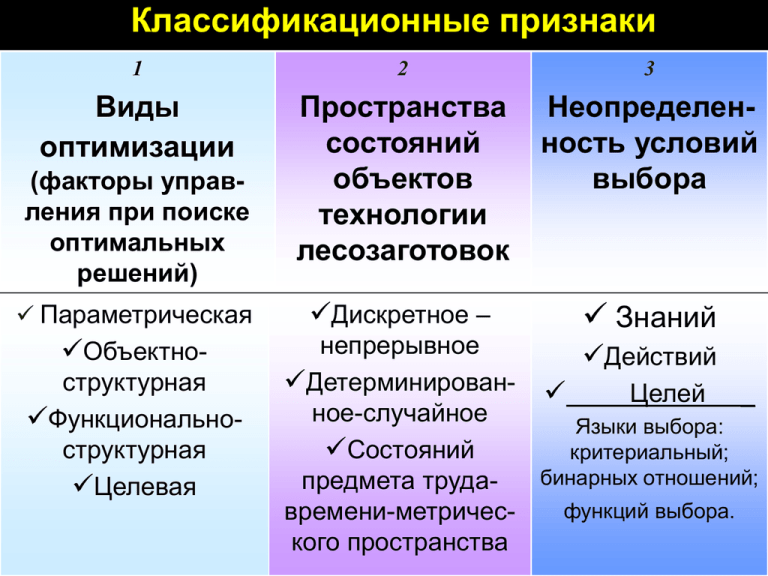
Классификационные признаки 1 2 3 Виды оптимизации Пространства состояний объектов технологии лесозаготовок Неопределенность условий выбора Дискретное – Знаний (факторы управления при поиске оптимальных решений) Параметрическая Объектноструктурная Функциональноструктурная Целевая непрерывное Действий Детерминирован- Целей _ ное-случайное Языки выбора: Состояний критериальный; бинарных отношений; предмета трудафункций выбора. времени-метрического пространства Назначение Повал дерева Функция Валка Поток Падающие деревья, энергия и информация для повала (действия по валке ) Структура Бензопила,гидроклин, дерево и их связи Функционал можно рассматривать как обобщение хорошо известного понятия функции, как функцию особого рода, в которой роль независимой переменной играет другая функция. Иначе, это функция от функции, где в качестве аргумента используется какая-либо функция, а в качестве значения функции (отклика на аргумент) является число. Функционал это математическое выражение критерия в задачах управления. В задачах оптимального управления различают функционал в виде интегральной суммы и интегральный функционал в виде определенного интеграла. 1 J ydx 0 y y=y(x) 0 A(a;0) участок B(b;0) x Отличительные признаки. Для задач оптимального управления характерны следующие особенности (в связи с тем, что здесь осуществляется выбор функции, обеспечивающей оптимальное управление, то несколько меняются ранее принятые обозначения). 1) Состояние объекта управленияx (процесса, лесозаготовительной машины) определяется n переменными x1, x2,…x . Если переменные i n1,, или n вектором состояния зависят от времени (как правило это именно так) xi = xi(t), x, то они называются фазовыми. 2) Управление объектом или процессом, определяющее изменение переменных u состояния (эволюция или движение), осуществляется переменными (параметрами) управления u1,u2,u3,…ur или вектором управления , определяющих положение "рулей", которые также могут быть выражены функцией времени. В ряде случаев оптимальное управление может быть обеспечено выбором соответствующей функции без воздействия рулей. Например, как в задаче Дидо. 3) В ряде случаев, dпри x писке оптимального процесса, объект управления f x (t ), u (t ), t описывается си-стемой дифференциальных уравнений, являющихся уравнениями dt состояния(связей) для x(k 1) f k x(k ), u (k ) непрерывных процессов или для дискретных процессов – системой разностных уравнений . Здесь k обозначает k-й момент времени или k-е состояние объекта в определенной позиции. 4) Имеются начальные и конечные граничные условия, наложенные на переменные состояния и управления, и требуется перевести объект из начального состояния в конечное. КЛАССЫ ФУНКЦИЙ. Классификация процессов. Аргумент х Функция y(x) Дискретный Непрерывный Дискретный Непрерывный Дискретная последовательность Дискретный процесс (квантование по уровню) Непрерывная последовательность, дискретная по уровню Непрерывный (аналоговый) процесс Отраслевыми примерами являются: дискретной последовательности - отображение состояний предмета труда (дерево, хлыст, сортимент и т.д.), иногда в виде графов, по маршруту технологического процесса (у пня, на волоке, на погрузочном пункте и т..д.); дискретного процесса – отображение изменения объема предмета труда (перерабатываемого лесопродукта) в каждом из состояний по координате расстояния маршрута технологического процесса; непрерывной последовательности – изменение объема предмета труда фиксируемое в каждой из позиций маршрута технологического процесса; непрерывного процесса – изменение объема предмета труда в процессе его переработки от начального состояния до конечного и Траектория перемещения предмета труда и (или) машин в трехмерном пространстве. Траектория изменения объема и перемещения предмета труда в пространстве и времени. Траектория изменения объема и перемещения предмета труда в четырехмерном пространстве. 9 Область допустимых решений задач синтеза технологических процессов. 3 1 2