Когерентное состояние
реклама

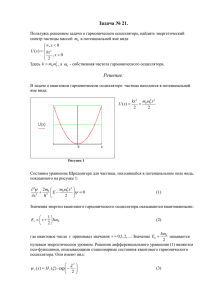
Приерететный национальный проект «Образование» ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Санкт-Петербургский государственный университет информационных технологий, механики и оптики Кафедра Компьютерной фотоники ЛЕКЦИИ по дисциплине ЕН.Ф.06 - ОПТИЧЕСКАЯ ФИЗИКА Доцент, к.т.н. - Е.В. Жукова 1 МОДУЛЬ 3. Лекция № 17 МОЛЕКУЛЯРНАЯ И КВАНТОВАЯ ОПТИКА ТЕМА 5. Основы квантовой оптики ТЕМА ЛЕКЦИИ: Понятие когерентных состояний в квантовой электродинамике. Сжатые состояния. Кооперативный эффект 2 Когерентное состояние - было открыто Шредингером (Schrцdinger, 1926) при рассмотрении гармонического осциллятора и определялось как состояние с минимальной неопределенностью. Когерентные состояния важны для описания квантового описания оптической когерентности. Термин когерентное состояние, используемое в квантовой оптике, ввел Глаубер (Glauber, 1963). Волновая функция, используемая для классического описания электромагнитного поля, должна иметь минимальную неопределенность для всех моментов времени. Таким свойством обладает волновая функция основного состояния смещенного простого гармонического осциллятора, представляющая собой волновой пакет, который совершает синусоидальные колебания в потенциальном поле. Соответствующий вектор состояния представляет собой когерентное состояние и обозначается как . .В квантовом состоянии гармонического осциллятора волновой пакет не расплывается, а его центр движется по классической траектории. 3 С классической точки зрения электромагнитное поле состоит из волн с определенными значениями амплитуды и фазы. Но при квантово-механическом описании поля это не так. В этом случае имеют место флуктуации как амплитуды, так и фазы поля. Электромагнитное поле в состоянии n с определенным числом частиц имеет вполне определенную амплитуду, но полностью неопределенную фазу, тогда как поле в когерентном состоянии имеет одинаковые величины неопределенностей для этих двух переменных. t полной системы удовлетворяет вектор состояния уравнению Шредингера d i t H t dt (1) t exp k ak *k ak 0 k k (2) 4 начальное состояние является вакуумным 0 0 k- единичный вектор поляризации, Ek - напряженность электрического поля, k - частота. t 1 k Ek dt drk k J r, t eik t ikr k (3) 0 k состояние поля излучения называется когерентным состоянием и так обозначается многомодовое когерентное состояние k exp k ak *k ak 0 k k k k (4) (5) когерентное состояние поля, как собственное состояние оператора уничтожения а с собственным значением 5 a (6) Состояние можно выразить определенным числом частиц n e 2 /2 e a n n! n n 0 0e 2 /2 (7) (9) через состояние с следующим образом D 0 D e 2 (8) / 2 a *a e e Согласно выражению (8) когерентное состояние получается в результате применения оператора смещения к вакуумному состоянию. Следовательно, когерентное состояние представляет собой смещенное основное состояние гармонического осциллятора. (10) 6 Предположим, что в момент времени t = 0 волновая функция (q, t ) 1 pq (n ) 2 (11) имеет вид волнового пакета с минимальной неопределенностью смещенного в положительном направлении q на величину q0. 14 (12) ( q,0) ( ) exp ( q q0 ) 2 2 Временная эволюция этого волнового пакета такова, что в последующие моменты времени плотность вероятности задается выражением 12 2 2 (13) ( q, t ) ( ) exp ( q q0 cos t ) 7 Рис. 1. Волновой пакет с минимальной неопределенностью в различные моменты времени в потенциальном поле гармонического осциллятора (а); соответствующее электрическое поле (б) 8 Свойства когерентных состояний поля среднее число фотонов в когерентном состоянии Рис. 2. Распределение фотонов p n 2 n ne pn n n n! n n n e n! (14) в когерентном состоянии 9 гамильтониан осциллятора в присутствии квадратичного потенциала p2 1 2 H kx eE0 ax bx2 2m 2 Рис. 3. Эволюция сжатого состояния простого гармонического осциллятора (15) p2 1 H k 2ebE0 x 2 eaE0 x 2m 2 (16) 10 Рис. 4. Потенциал, отмеченный пунктирной линей, вызывает осцилляции частицы с массой m и зарядом е относительно положения х = 0. Приложение постоянного электрического поля эквивалентно растяжению пружины до нового положения равновесия , относительно которого будет совершать осцилляции точечный заряд 11 Рис. 5. Потенциал осциллятора сначала смещается постоянным электрическим полем, а затем “искажается” барьерами, которые ограничивают осцилляции заряда в пределах конечной области (а); потенциал плоского гармонического осциллятора смещается и “сужается” квадратичным потенциалом смещения (б) 12 Рис. 6. Сжатие волнового пакета смещенным “суженным” квадратичным потенциалом плоского гармонического осциллятора 13 Сжатые состояния и соотношение неопределенности Согласно принципу неопределенности Гейзенберга произведение неопределенностей в определении средних значений двух переменных А и В задается выражением рассмотрим квантованное одномодовое электрическое поле частотой it Et E ae a eit (17) Введем эрмитовые операторы амплитуды 1 X1 a a 2 1 (19) a a 2 операторы представляют собой операторы безразмерных координаты и импульса: (18) X1 14 2 / m x a a 2 (20) E(t ) 2 E X 1 cos t X 2 sin t Условием сжатого неравенства 2m a a 2i p состояния (21) 1 (22) X1X 2 4 является X i (i=1 или 2) (23) выполнение (24) идеальное сжатое состояние 1 X1X 2 4 (25) 15 Рис. 7. Области неопределенности и соответствующие им графики зависимости электрического поля от времени: когерентное состояние (а); сжатое состояние с уменьшенным шумом в (б); сжатое состояние с уменьшенным шумом в (в) 16 Квантовые неразрушающие измерения - измерения, не изменяющие состояния исследуемой системы, если оно является собственным для оператора измеряемой величины. Квантовые неразрушающие измерения представляет собой реализацию идеального квантового измерения, то есть точного измерения числа фотонов, при этом не потерять ни одного за счет поглощения части фотонов. Для таких изменений необходимо учитывать квантовые свойства макроскопических объектов. Устройства, регистрирующие единичные кванты, например, перспективны как элементы оптических компьютеров 17 Квантовая метрология - наука об измерениях, базирующаяся на квантовых явлениях. Основная проблема квантовой метрологии – это установление естественной системы единиц физических величин на основе фундаментальных констант. Главное направления в квантовой метрологии - это разработка и реализация квантовых эталонов, установление соответствия между размерами единиц, воспроизводимых различными кантовыми эталонами, а также преемственности между ними и традиционными эталонами. Важное направление в квантовой метрологии выявление и изучение погрешностей квантовых эталонов, вызываемых ограничениями квантового характера (соотношением неопределенностей). Квантовыми эталонами единиц физических величин в .системе СИ служат, например, единица времени (секунда), воспроизводимая с помощью квантового цезиевого эталона частоты; единица длины, поддерживаемая излучением 86Kr. С квантовой метрологией связана разработка измерений с наивысшей точностью и минимальным порогом чувствительности. Например, при работе с квантовыми интерферометрами порог чувствительности снижен вплоть до 10-14 В. 18 Кооперативный эффект - явления в многочастичной системе, связанные с когерентным (согласованным) взаимодействием большого числа частиц. Существуют явления и эффекты, которые зависят от состояния и взаимодействия группы атомов, причем групповое или коллективное поведение атомной системы может быть относительно простым. Тогда исследовать явление можно путем суммирования вкладов от индивидуальных атомов в общее поле, и полагать что атомы действут почти независимо друг от друга. В других случаях важно учесть влияние каждого атома на остальные, поскольку это существенно меняет поведение каждого из них. Такие эффекты называют кооперативными. 19 Пример – сверхтекучесть и сверхпроводимость – это примеры кооперативных явлений, при которых квантовая когерентность проявляется макроскопических масштабах, а именно посредством электрон-фононного взаимодействия. Существуют неравновесные кооперативные явления, возникающие в открытых системах и их существование связано с диссипацией энергии. Излучение лазера – пример неравновесного кооперативного явления, когда при достаточно высокой степени неравновесности (мощности накачки) бесструктурное состояние системы становится неустойчивым по отношению к малым флуктуациям, что сопровождается генерацией излучения. Литература: 1. Скалли М.О., Зубайри М.С. Квантовая оптика. М.:ФИЗМАТЛИТ, 2003 г. 20