N-i+1

Решение задач С1, С2 и С3
Золотарева Е.В.
С1. Требовалось написать программу, которая вводит с клавиатуры
натуральное число N, не превышающее 109, и выводит сумму чётных цифр в
десятичной записи этого числа или 0, если чётных цифр нет. Программист
торопился и написал программу неправильно. Вот она:
var N: longint;
s: integer;
begin
readln(N);
(1)
s := 0;
(2)
while N > 1 do begin
(3)
if N mod 2 = 0 then begin
(4)
s := N mod 10;
(5)
end;
(6)
N := N div 10;
(7)
end;
(8)
write(s);
(9)
end.
Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 1984.
2. Приведите пример числа, при вводе которого программа выдаст верный
ответ.
3. Найдите в программе все ошибки (их может быть одна или несколько).
Для каждой ошибки выпишите строку, в которой она допущена, и приведите
эту же строку в исправленном виде.
C1. Требовалось написать программу, которая получает на вход натуральное
число N, не превосходящее 109, и выводит число, которое получается из N после
удаления всех единиц; порядок остальных цифр при этом не меняется. Например,
число 19520125 должно быть преобразовано в число 952025. Число, в котором все
цифры – единицы и нули, должно быть преобразовано в 0. Незначащие нули в
старших разрядах полученного числа печатать не нужно. Программист торопился и
написал программу неправильно.
var N, R, T: longint;
d: integer;
begin
readln(N);
R:=0;
T:=1;
while N>0 do begin
d := N mod 10;
if d<>1 then begin
R := R + d*T;
T := T+1
end;
N := N div 10;
end;
writeln(T);
end.
Последовательно
выполните
следующее.
при вводе числа 314
программа
выводит 3
•Напишите,
что ответ).
выведет эта программа при
(неправильный
вводе числа 314.
•Найдите все ошибки в этой программе (их
Ошибкабыть
1: выводить
значение
может
одна или следует
несколько).
Для
переменной
R:
каждой
ошибки:
строка:
writeln(T);
1)
Выпишите
строку, в которой сделана
исправление: writeln(R);
ошибка.
переменной
2) Ошибка
Укажите,2: изменение
как исправить
ошибкуT –в
теле циклаправильный вариант
приведите
строка: T := T+1
строки.
исправление:
T := T*10
Обратите
внимание,
что требуется найти
ошибки в имеющейся программе, а не
написать свою, возможно, использующую
другой алгоритм решения.
С1. Требовалось написать программу, при выполнении которой с
клавиатуры вводится натуральное число, не превосходящее 108, и
выводится его первая (старшая) цифра. Ученик написал такую программу:
var n: longint;
begin
read(n);
while n>10 do begin
n := n mod 10
end;
write(n);
end.
•при вводе числа 1984 программа
выводит 4 (неправильный ответ).
•программа работает верно для любого числа, у которого старшая
Последовательно
выполните
цифра равна младшей,
в том числеследующее.
для любого однозначного числа
•Напишите, что выведет эта программа при вводе числа 1984.
•Приведите
пример числа, при вводе которого программа
Ошибка 1: в условии цикла должно быть строгое равенство:
выдаст
верный
ответ.
строка: while
n>10
do begin
исправление:
n>=10 все
do ошибки
begin (их может быть одна или
•Найдите вwhile
программе
Ошибка 2: операция в теле цикла
несколько).
строка: n := n mod 10
исправление: n := n div 10
var x: real;
begin
readln(x);
if x>=-3 then
if x<=9 then
if x>1 then
ДА
write('не принадлежит')
НЕТ
Х>=-3
В столбцах условий укажите
else
write('принадлежит') «да», если условие выполнится,
«нет», если условие не выполнится,
ДА
НЕТ
end.
«—» (прочерк), если условие не будет проверяться,
С1
Х<=9
«не изв.», если программа ведет себя
по-разному для разных значений, принадлежащих
данной области.
НЕТ
ДА
Х>1
В столбце «Программа выведет»
Если программа ничего не выводит,
НЕзначений,
напишите «—»
(прочерк). Если для разных
принадле
принадле
принадлежащихжит
области, будут выведены
разные
жит
тексты, напишите «не изв.».
В последнем столбце укажите «Да» или «Нет».
НЕТ
Х>=-3
НЕТ
ДА
Х<=9
НЕТ
ДА
Х>1
ДА
Не
принадл
принадл
Обл
Усл 1
(x>=-3)
Усл 2
(x<=9)
Усл 3
(x>1)
Программа
выдает
Область
обрабатыва
ется верно
А
Нет
-
-
-
нет
В
Да
Да
Нет
Принадлеж
Да
С
Да
Да
Да
Не принадл
Да
D
Да
Да
Да
Не принадл
Нет
E
Да
Нет
-
-
Нет
var x: real;
begin
readln(x);
if x>=-3 then
if x<=9 then
if x>1 then
write('не принадлежит')
else
write('принадлежит')
end.
С1
If (x=>-3) and (x<=1) or (x>=5) and (x<=9) then
write (‘принадлежит’)
else
write (‘не принадлежит’);
var x,y: real;
begin
readln(x,y);
if y>=x then
if y>=0 then
if y<=2-x*x then
write('принадлежит')
else
write('не принадлежит')
end.
НЕТ
ДА
У>=Х
НЕТ
У>=0
НЕТ
Не
принадлеж
ит
ДА
У<=2x*x
ДА
Принадлеж
ит
НЕТ
У>=Х
НЕТ
ДА
У>=0
НЕТ
ДА
У<=2x*x
НЕТ
Обл
аст
ь
A
B
C
D
E
F
G
ДА
ДА
y>=
x?
y>=0
?
y<=2x*x?
вывод
верно
?
да
да
нет
нет
да
да
нет
да
нет
–
–
да
нет
–
нет
–
–
–
да
–
–
не принадл
–
–
–
принадл
–
–
да
нет
нет
нет
да
нет
нет
var x,y: real;
begin
readln(x,y);
if y>=x then
if y>=0 then
if y<=2-x*x then
write('принадлежит')
else
write('не принадлежит')
end.
(y <=2-x*x) and ((y>=x) or (y>=0))
Требовалось написать программу, при выполнении которой с клавиатуры
считываются координаты точки на плоскости (х, у - действительные числа) и
определяется принадлежность этой точки заданной закрашенной области
(включая границы). Ученик написал такую программу:
var x, y: real;
begin
readln(x,у);
if у >= x*x-6 then begin
if x*x + у* у <=16 then
write('принадлежит')
end
else
if x >= 0 then
write('принадлежит')
else write('не принадлежит')
end.
При проверке работы программа выполнялась по шагам для некоторых контрольных
значений х и у, при этом был заполнен протокол тестирования. В результате
неаккуратного обращения протокол был испорчен, частично сохранились только
четыре строки:
Область
Условие 1
(y >= x*x-6)
Условие 2
(x*x+y*y <= 16)
Условие 3
(x >= 0)
да
Вывод
Верно
—
–
принадлежит
нет
не принадлежит
да
да
Последовательно выполните следующее.
•Восстановите уцелевшие строки протокола, заполнив все клетки
таблицы. Там, где содержание восстанавливается неоднозначно,
запишите любое возможное значение. Например, если для
нескольких областей получается одинаковая строка таблицы, укажите
в графе «Область» любую из этих областей.
•Укажите, как нужно доработать программу, чтобы не было случаев её
неправильной работы. (Это можно сделать несколькими способами,
достаточно указать любой способ доработки исходной программы.)
Область
Условие 1
(y >= x*x-6)
Условие 2
(x*x+y*y <= 16)
Условие 3
(x >= 0)
Вывод
да
—
принадлежит
нет
не принадлежит
да
–
НЕТ
да
ДА
НЕТ
НЕТ
Верно
У>=x*x-6
НЕТ
X>=0
ДА
x2+y2<16
ДА
ДА
max:=99;
for i:=1 to N do
if (max<a[i]) and (a[i]>99) and
(a[i]<1000) and (a[i] mod 9<>0) then
max:=a[i];
If max=99 then writeln (‘не найдено’)
else Writeln(max);
end.
…:=…;
for i:=… to … do
тело цикла
Writeln(…);
If
…=… then Writeln(‘не найдено’)
end. writeln (…);
else
end.
С2. Дан массив, содержащий 2014 положительных целых чисел.
Симметричной парой называются два элемента, которые находятся на
равном расстоянии от концов массива. Например, 1-й и 2014-й элементы, 2-й
и 2013-й и т. д. Порядок элементов в симметричной паре не учитывается:
элементы на 1 и 2014 местах – это та же самая пара, что и элементы на 2014
и 1 местах. Напишите на одном из языков программирования программу,
которая подсчитывает в массиве количество симметричных пар, у которых
сумма элементов больше 20. Программа должна вывести одно число –
количество отобранных симметричных пар. Исходные данные объявлены
так, как показано ниже. Запрещается использовать переменные, не
описанные ниже, но разрешается не использовать часть из описанных
const
переменных.
N=2014;
var a: array [1..N] of integer;
i, j, k: integer;
begin
for i:=1 to N do
readln(a[i]);
…
end.
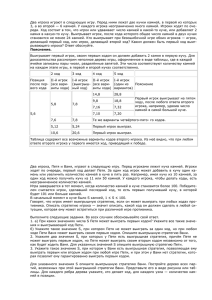
•В цикле нужно находить сумму элемента массива (a[i]) с
симметричным ему элементом, который имеет номер N-i+1 (так
чтобы для i=1 мы получили N).
•Если выполняется условие, что эта сумма больше 20, то
увеличиваем счётчик – переменную k.
ВАЖНО: поскольку мы просматриваем массив фактически сразу с
двух концов, нужно остановиться на середине, то есть в цикле
сделать N div 2 шагов, а не N:
k:=0;
for i:=1 to N div 2 do
if a[i]+a[N+1-i] > 20 then
k:= k + 1;
writeln(k);
end.
С3
Два игрока, Петя и Ваня, играют в следующую игру. Перед
игроками лежит куча камней. Игроки ходят по очереди, первый
ход делает Петя. За один ход игрок может добавить в кучу один
камень или увеличить количество камней в куче в два раза.
Например, имея кучу из 15 камней, за один ход можно получить
кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы,
есть неограниченное количество камней. Игра завершается в
тот момент, когда количество камней в куче становится
не менее 22. Победителем считается игрок, сделавший последний
ход, то есть первым получивший кучу, в которой будет 22 или
больше камней. В начальный момент в куче было S камней,
1 ≤ S ≤ 21. Будем говорить, что игрок имеет выигрышную
стратегию, если он может выиграть при любых ходах против‐
ника. Описать стратегию игрока – значит описать, какой ход он
должен сделать в любой ситуации, которая ему может
встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях
обосновывайте свой ответ.
1. а) Укажите все такие значения числа S, при которых Петя
может выиграть в один ход. Обоснуйте, что найдены все
нужные значения S, и укажите выигрывающий ход для
каждого указанного значения S.
б) Укажите такое значение S, при котором Петя не может
выиграть за один ход, но при любом ходе Пети Ваня может
выиграть своим первым ходом. Опишите выигрышную
стратегию Вани.
2. Укажите два таких значения S, при которых у Пети есть
выигрышная стратегия, причём
– Петя не может выиграть за один ход, и
– Петя может выиграть своим вторым ходом, независимо от
того, как будет ходить Ваня.
Для каждого указанного значения S опишите выигрышную
стратегию Пети.
3. Укажите значение S, при котором:
– у Вани есть выигрышная стратегия, позволяющая ему
выиграть первым или вторым ходом при любой игре Пети, и
– у Вани нет стратегии, которая позволит ему
гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию
Вани.
Постройте дерево всех партий, возможных при этой
выигрышной стратегии Вани (в виде рисунка или таблицы).
На рёбрах дерева указывайте, кто делает ход, в узлах
– количество камней в куче.
При первом чтении условие этой задачи поражает и отпугивает своей
длиной — почти страница текста.
Но на самом деле она довольно проста, и, что самое главное, в ней
требуется понимание сути игровой стратегии и минимум рутинной
работы. В результате вероятность случайной ошибки довольно низка.
1. а) Укажите все такие значения числа S, при которых
Петя может выиграть в один ход
б) Укажите такое значение S, при котором Петя не
может выиграть за один ход, но при любом ходе
Пети Ваня может выиграть своим первым ходом.
+1
*2
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21
В
П П П
П
П
П
П
П
П
П
П
1
1
1
1
1
1
1
1
1
1
1
1
1
а) Петя
за один ход
при любом
S > 10.что
Он
При
S = 10 может
Петя невыиграть
может выиграть
в один
ход, потому
должен
увеличить
вдвое
число вкамней,
при этом вравно
куче всегда
при его ходе
“+1” число
камней
куче становится
11
получится
неаменее
22 камней.
(меньше 22),
при ходе
“*2” число камней в куче становится
равно 20 (также меньше 22). Других возможных ходов у Пети
нет. Из любой позиции после одного хода Пети (это может быть 11 или 20) Ваня может выиграть своим первым
ходом, удвоив количество камней в куче.
2. Укажите два таких значения S, при которых у Пети есть
выигрышная стратегия, причём
– Петя не может выиграть за один ход, и
– Петя может выиграть своим вторым ходом, независимо от того,
как будет ходить Ваня.
Для каждого указанного значения S опишите выигрышную
стратегию Пети.
+1
*2
*2
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21
П
П
В
П П П
П
П
П
П
П
П
П
П
2
2
1
1
1
1
1
1
1
1
1
1
1
1
+1
Из позиций S = 9 и S = 5 Петя не может выиграть в один ход, но
Петя может выиграть своим вторым ходом, независимо от
того, как будет ходить Ваня. При S = 9 ходом “+1” Пете нужно
перевести игру в позицию S = 10, которая является
проигрышной (см. ответ на вопрос 1б). При S = 5 Петя переводит игру в ту же позицию ходом “*2”.
Укажите значение S, при котором:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети, и
– у Вани нет стратегии, которая позволит ему гарантированно
выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
+1
*2
+1
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21
П
В
П
В
П П П
П
П
П
П
П
П
П
П
2
2
2
1
1
1
1
1
1
1
1
1
1
*2
1
1
В позиции S = 8 у Вани есть выигрышная стратегия, которая
позволяет ему выиграть первым или вторым ходом. Если Петя
выбирает ход “+1”, в куче становится 9 камней, и Ваня
выигрывает на втором ходу (см. ответ на вопрос 2). Если Петя
выбирает ход “*2”, Ваня выигрывает первым ходом, удвоив
число камней в куче.
1 а) Петя может выиграть за один ход при любом S > 10. Он
должен увеличить вдвое число камней, при этом в куче всегда
получится не менее 22 камней.
1б) При S = 10 Петя не может выиграть в один ход, потому
что при его ходе “+1” число камней в куче становится равно 11
(меньше 22), а при ходе “*2” число камней в куче становится
равно 20 (также меньше 22). Других возможных ходов у Пети
нет. Из любой позиции после одного хода Пети (это может
быть 11 или 20) Ваня может выиграть своим первым ходом,
удвоив количество камней в куче.
2) Из позиций S = 9 и S = 5 Петя не может выиграть в один ход,
но Петя может выиграть своим вторым ходом, независимо
от того, как будет ходить Ваня. При S = 9 ходом “+1” Пете
нужно перевести игру в позицию S = 10, которая является
проигрышной (см. ответ на вопрос 1б). При S = 5 Петя переводит игру в ту же позицию ходом “*2”.
В позиции S = 8 у Вани есть выигрышная стратегия, которая
позволяет ему выиграть первым или вторым ходом. Если
Петя выбирает ход “+1”, в куче становится 9 камней, и Ваня
выигрывает на втором ходу (см. ответ на вопрос 2). Если
Петя выбирает ход “*2”, Ваня выигрывает первым ходом,
удвоив число камней в куче.
•Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками
лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За
один ход игрок может добавить в кучу один или пять камней или увеличить
количество камней в куче в три раза. Например, имея кучу из 15 камней,
за один ход можно получить кучу из 16, 20 или 45 камней. У каждого
игрока, чтобы делать ходы, есть неограниченное количество камней. Игра
завершается в тот момент, когда количество камней в куче становится не
менее 41. Победителем считается игрок, сделавший последний ход, то
есть первым получивший кучу, в которой будет 41 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 40.
1.При каких S:
1а) Петя выигрывает первым ходом;
1б) Ваня выигрывает первым ходом?
2. Назовите два значения S, при которых Петя может выиграть своим
вторым ходом?
3. Назовите два значения S, при которых Ваня выигрывает своим
первым или вторым ходом?