Оптимальное планирование инструкций для процессоров семейства IA-64 с использованием алгоритма A*

Оптимальное планирование
инструкций для процессоров
семейства IA-64 с
использованием алгоритма A*
Дипломная работа студента 545 группы
Галанова Сергей Евгеньевича
Научный руководитель: Булычев Дмитрий
Юрьевич
Рецензент: Фоминых Николай Федорович
Задача планирования




Планирование выполняется в конце компиляции,
после выбора инструкций и распределения
регистров
В ходе планирования происходит построение
плана исполнения программы - переупорядочение
инструкций и их распределение по
вычислительным устройствам
Целью является построение оптимального плана,
то есть плана с минимальным временем
исполнения
Задача оптимального планирования NP-трудна
Существующие подходы

Списковое планирование (list scheduling) –
применяется в промышленных компиляторах, но
дает субоптимальные результаты

Целочисленное линейное программирование

Программирование ограничений

Метод ветвей и границ
Постановка задачи


На вход подается готовый ассемблерный код для
процессора Intel Itanium 2
Требуется выполнить его оптимальное локальное
планирование, то есть построить для каждого
базового блока план с минимальным временем
исполнения (либо оставить исходный план, если
планировщику не удалось завершиться за
разумное время) и выдать новый ассемблерный
код
Обзор EPIC



EPIC (Explicitly Parallel Instruction Computing) –
новый класс машинных архитектур, являющийся
усовершенствованием класса VLIW (Very Long
Instruction Word)
Информация о параллелизме инструкций и
распределении их по устройствам рассчитывается
компилятором статически
Требуется обеспечить совместимость кода между
разными представителями архитектуры, поэтому
должны накладываться специальные ограничения
на кодирование инструкций
Обзор архитектуры IA-64




Архитектура IA-64 реализует принципы EPIC
Инструкции упакованы в пакеты (bundles) по три
инструкции в каждом
Для каждого пакета указывается шаблон,
задающий устройства для инструкций и границы
групп параллельно исполняемых инструкций
Поддерживается предикативное и спекулятивное
исполнение
Особенности Itanium 2



Может запускать до шести параллельных
инструкций за такт
Латентность большинства арифметико-логических
операций – 1 такт, операций с плавающей точкой –
4 такта, загрузок и выгрузок (для кэша 1 уровня) – 1
такт, мультимедийных операций – 2-3 такта
Может быть запущено до двух операций с
плавающей точкой за такт, до двух загрузок за такт,
до двух выгрузок за такт
Пример кода
{ mmi
add r1 = r2, r3
add r4 = r5, r6
add r7 = r8, r9
}
{ m.mi
add r9 = r2, r5 ;;
ld4 r2 = [r1]
add r8 = r9, r10
}
{ mfi.
sub r6 = r7, r4
fadd f3 = f4, f5
add r12 = r1, r4
}
// => M0
// => M1
// => I0
// => M2
// => M0
// => I0
// => M1
// => F0
// => I1
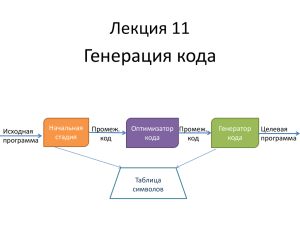
Общая структура планировщика


Чтение исходного ассемблерного кода и
выделение блоков
Анализ зависимостей в каждом блоке и построение
дэга зависимостей

Планирование плана для каждого блока

Построение результирующего ассемблерного кода
Пространство и граф поиска






Пространство поиска состоит из частичных планов
К частичному плану можно применять
элементарные операции issueOp и endGroup
В вершинах графа поиска находятся частичные
планы
Два плана соединены дугой, если второй получен
из первого применением элементарной операции
Есть дополнительная конечная вершина, в которую
входят дуги из полных планов
Расстояние между двумя планами равно разности
их длин (в тактах)
Алгоритм A*



Является обобщением алгоритма Дейкстры
При выборе направления обхода используется не
длина пройденного пути, а оцениваемая длина
оптимального пути, которая складывается из
известной длины текущего пути и эвристической
оценки длины оптимального пути из текущей точки
до концевой
Если эвристика не переоценивает длину, получится
оптимальный путь
Поиск оптимального плана


Для поиска оптимального плана применим
алгоритм A* к графу поиска
Необходимо найти хорошую эвристику,
оценивающую расстояние (в тактах) от заданной
точки до конечной
Эвристика критического пути

Число тактов, требуемое для набора инструкций не
может быть меньше длины критического пути в
дэге зависимостей

Можно взять в качестве эвристики эту длину

Она хорошо работает для «густых» дэгов

Плохо работает для блоков, в которых мало
зависимостей
Эвристика доступных ресурсов



Определяется число инструкций каждого класса
Для каждого класса определяется минимальное
число тактов, требуемое для выполнения
соответствующего набора инструкций
Выбирается максимум
Гибридная эвристика




Объединяет достоинства эвристик критического
пути и доступных ресурсов
Для каждой инструкции определяется нижняя
граница номеров тактов, в которых она может быть
запущена (на основе критических путей в дэге)
Для каждой нижней границы определяется
минимальное число дополнительных тактов,
требуемое для запуска остальных инструкций (на
основе эвристики доступных ресурсов)
Выбирается максимум
Дополнительная эвристика




У точек с равными основными эвристиками
сравниваются дополнительные эвристики
Для каждого возможного значения длины
критического пути среди всех вершин дэга
подсчитывается количество вершин, для которых
достигается это значение
Полученные числа выстраиваются в порядке
убывания длин критических путей
Полученный кортеж является эвристикой
Некоторые оптимизации

Оптимизации размещения пустых операций

Рудиментарное выделение изоморфных поддэгов

На множестве частичных планов вводится
отношение (нетривиального) равенства: два плана
равны, если их соответствующие группы
инструкций одинаковы с точностью до
перестановки инструкций (используется
оптимизированное внутреннее представление
плана для эффективного выполнения этой
проверки)
Результаты
• Тестирование проводилось на пакете mesa из набора
тестов SPEC FP, откомпилированном компиляторами
open64 и gcc.
open64
gcc
Блоков
27747
11420
Уже оптимально
25636 (92.4%)
8276 (72.5%)
Улучшено
1494 (5.4%)
2086 (18.3%)
Не завершилось
184 (0.66%)
276 (2.4%)
Перспективы дальнейшего
развития

Улучшение эвристик

Сокращение числа вариантов

Более точный анализ зависимостей

Обобщение на произвольную архитектуру
Спасибо за внимание
Вопросы?