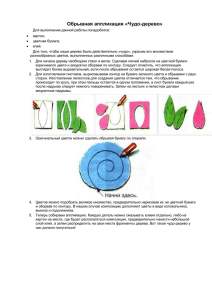
1+2 x 1+3 

Абстракция

Абстракция основана на




обобщении посредством введения имени вместо
значения и
уточнении (конкретизации) посредством подстановки
другого значения вместо данного имени
Абстрагирующее имя явно или неявно привязано к
определенному типу значений.
Примеры:
1+2
1+3
1+x: x 
( y, x)
y  x : x, y 
op( y, x)
Абстракция в императивных языках программирования




Переменная в ИП – синоним ячейки памяти
Компилятор абстрагирует связь имя-значение от
конкретной ячейки памяти.
Типы данных контролируют корректность связи
имя-значение.
Компилятор контролирует корректность
размещения значения в той или иной ячейке
памяти (выравнивание, тип выделяемой памяти)
Абстракция в императивных языках высокого уровня

Абстрактный тип данных




Представление данных скрыто от пользователя и
может быть заменено альтернативным.
Любое из этих представлений должно реализовывать
методы доступа к данным.
Эти методы доступа должны удовлетворять
определенным инвариантам («законам»).
Пример:


«Маршрут» как АТД в системе управления
транспортом: getStartingPoint, getEndingPoint,
getDistance, …
Метод getDistance для составного маршрута должен
удовлетворять неравенству треугольника
Абстракция в императивных языках высокого уровня

Модули

ООП


Инкапсуляция
Задание:

Придумать и написать на С++ заголовочный файл,
реализующий абстрактный тип данных
Лямбда-исчисление
 Алонсо Черч, 1930 г.
 Модель «единицы вычислимости»
 Представляет собой язык, основанный на
«чистой» абстракции
 Математическая модель абстракции

Сама абстракция становится объектом
Лямбда-выражение

Используем «форму Бэкуса» для задания синтаксиса


<выражение> ::= <имя>|<функция>|<аппликация>
Имя – произвольный набор символов (не только
«идентификатор»)

фред

x1

12z



@>
Функция


Абстракция над лямбда-выражением

<функция> ::= λ<имя>.<тело>

<тело> ::= <выражение>
Примеры:

λx.x

λfirst.λsecond.first

λf.λa.(f a)

<Имя> называется «связанной переменной».

Похоже на «формальный параметр» ИП


<Тело> - произвольное лямбда-выражение, в т.ч. и
другая функция.
Функция – безымянна!
Аппликация

Применение функции к выражению

<аппликация> ::= (<функциональное выражение> <выражение-аргумент>)

Примеры:
( x.(2 x  1) 13)
( f .(f )  x.sin 3 x)
( x.x  a.b.b)

Терминология:

(Ф А) – «связанная пара» или «Ф применяется к А»
Вычисление аппликации





<аппликация> ::= (<функциональное выражение> <выражение-аргумент>)
1. В функциональном выражении проводятся
вычисления всех аппликаций, результат должен быть
функцией
2. В теле функции связанная переменная заменяется
на

Результат вычисления выражения-аргумента

Само выражение-аргумент в «текстуальной» форме
Первый способ называется «аппликативный
порядок»
Второй способ называется «нормальный порядок»
Тождественная функция
 x.x




x слева – связанная переменная (имя, играющее роль
связанной переменной)
x справа – имя
Аппликация тождественной функции возвращает
выражение-аргумент.
При нормальном порядке вычисления аргумент
возвращается невычисленным.
Каррирование функций

Рассмотрим пример:
a.b.a  b

Аппликация
( a.b.a  b 5)

дает
b.5  b


Функция многих переменных представляется как
суперпозиция лямбда-функций.
«Каррирование» (currying) – в честь Хаскеля Карри (хотя
придумал Шенфинкель).