Двугранный угол. Перпендикулярность плоскостей.

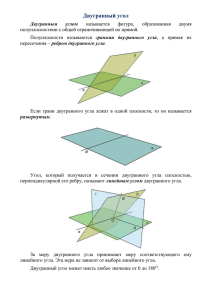
Двугранный угол. Перпендикулярность плоскостей.
Двугранный угол
Двугранным углом называется фигура, образованная
двумя полуплоскостями с общей граничной прямой и
частью пространства, для которой эти полуплоскости
служат границей.
Полуплоскости называются гранями двугранного угла,
общая граничная прямая полуплоскостей называется
ребром двугранного угла.
Двугранный угол, ребро которого есть прямая AB, а гранями
являются полуплоскости  и , обозначается AB (или
TABE, если на разных его гранях отмечены точки T и E)
Линейным углом двугранного угла называется угол,
сторонами которого являются лучи с общим началом на
ребре двугранного угла, которые проведены в его гранях
перпендикулярно ребру.
Линейный угол
двугранного угла
Градусная мера
двугранного угла
Градусной мерой двугранного угла называется градусная
мера его линейного угла.
Двугранный угол называется прямым (острым, тупым), если
его градусная мера равна 90 (меньше 90, больше 90).
Под двугранным углом понимается тот линейный угол,
градусная мера  которого удовлетворяет условию
0<<180
Вместо «двугранный угол, градусная мера которого равна
» коротко говорят «двугранный угол, равный »
Двугранный угол. Перпендикулярность плоскостей.
Углом между пересекающимися плоскостями называется
угол между прямыми, проведёнными в плоскостях
перпендикулярно их линии пересечения через некоторую
точку.
Угол между
пересекающимися
плоскостями
Если плоскости параллельны, то угол между ними
считается равным 0.
Угол между пересекающимися плоскостями удовлетворяет
условию 0<(;)90
Перпендикулярные Две плоскости называются перпендикулярными, если угол
плоскости
между ними равен 90
Если одна из двух плоскостей проходит через прямую,
перпендикулярную другой плоскости, то эти плоскости
перпендикулярны.
Признак
перпендикулярнос
ти плоскостей
Свойство прямой,
проведённой в
одной из
перпендикулярных
плоскостей
перпендикулярно
прямой, по
которой они
пересекаются.
Прямая, проведённая в одной из перпендикулярных
плоскостей перпендикулярно прямой, по которой они
пересекаются, перпендикулярна другой плоскости.
Двугранный угол. Перпендикулярность плоскостей.
Площадь Sорт ортогональной проекции треугольника ABC на
плоскость равна произведению его площади S на косинус
угла  между плоскостью треугольника и плоскостью
проекции Sорт=Scos.
Формула площади
ортогональной
проекции
треугольника
Свойство
пирамиды,
боковые грани
которой образуют
равные углы с
плоскостью
основания
Если в пирамиде двугранные углы при основании равны, то
основание перпендикуляра, проведённого из вершины
пирамиды к плоскости основания, совпадает с центром
окружности, вписанной в многоугольник основания
пирамиды