КСЕ лек 1.
реклама
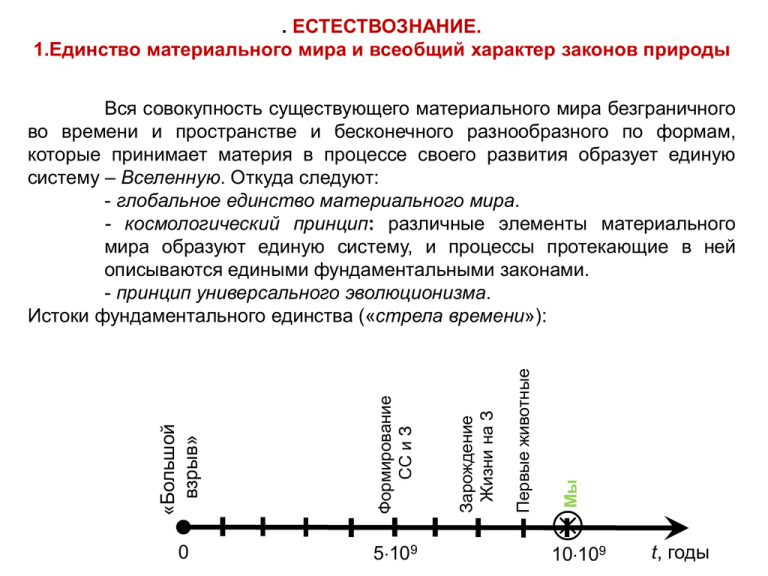
. ЕСТЕСТВОЗНАНИЕ. 1.Единство материального мира и всеобщий характер законов природы Мы Первые животные Формирование СС и З 0 5109 Зарождение Жизни на З «Большой взрыв» Вся совокупность существующего материального мира безграничного во времени и пространстве и бесконечного разнообразного по формам, которые принимает материя в процессе своего развития образует единую систему – Вселенную. Откуда следуют: - глобальное единство материального мира. - космологический принцип: различные элементы материального мира образуют единую систему, и процессы протекающие в ней описываются едиными фундаментальными законами. - принцип универсального эволюционизма. Истоки фундаментального единства («стрела времени»): 1010 9 t, годы Размеры, м 2. Разнообразие объектов материального мира. Микро-, макро- и мегомиры Диапазон масс и размеров материальных объектов во Вселенной Наблюдаемая Вселенная 1030 1020 1020 Солнце 1010 Земля 100 10-10 Молекулы Живые организмы Электрон 10-20 10-30 10-20 10-10 100 1010 1020 1030 1040 1050 Масса, кг 10-20 Молния 10-10 «зона жизни» Радиоактивный распад ядра атома Тепловое движение молекул 100 1010 1020 1030 Взрыв сверхновой звезды Вращение Земли Сильное землетрясение Термоядерный взрыв Ядерный взрыв Диапазон энергий материальных процессов во Вселенной 1040 Энергия, Дж 10-22 10-18 Возраст Вселенной Время жизни человека Время жизни элементарных частиц Диапазон длительностей различных процессов во Вселенной 10-6 10-4 10-2 1 102 1 103 104 106 106 109 t, годы t, с 100 лет – 8,64106 с 10-15 м 106 м 10-6 м 1030 м Микромир Макромир Мегамир Элементарные частицы, атомы и молекулы, ….. Макротела, ….., планеты. Звезды, галактики, Вселенная. Неклассическая механика (квантовая физика, физика элементарных частиц, квантовая статистика…. ), химия. mэ=0,9110-30 кг, mр=1,6710-27 кг, Классическая физика, биология, химия, науки о Земле, …. Теория относительности Эйнштейна (гравитация + СТО), астрономия, астрофизика, …. , Космология. МЗ 1013 кг, RЗ = 6,4 106 м Солнце: Т 107 К, RС = 7 108 м, МС 1030 кг. Галактики: Nзв 109 – 1012 шт, МГ 1041 кг, NГал 1011 шт, Синергетика 3. Дифференциация наук. Естествознание КОНЦЕПЦИЯ (от лат. conceptio – понимание, система), определенный способ понимания, трактовки каких-либо явлений, основная точка зрения, руководящая идея для их освещения; ведущий замысел, конструктивный принцип различных видов деятельности. ЕСТЕСТВОЗНАНИЕ в современном понимании – это совокупность наук о природе как системе тел, «материальных реальностей», находящихся во взаимной связи, взаимодействии и движении. Науки, входящие в естествознание: ФИЗИКА – исследует наиболее простые и потому наиболее фундаментальные уровни организации материи. КОСМОЛОГИЯ – раздел физической науки, исследующей Вселенную как целое и её эволюцию. ХИМИЯ – исследует материю на атомарном молекулярном уровне. БИОЛОГИЯ – исследует клеточный уровень организации живой материи и всё многообразие живых организмов. НАУКИ О ЗЕМЛЕ (геология, геофизика… ) – исследующие процессы планетарного масштаба, происходящие во всех сферах Земли. Общая структура современного естествознания Фундаментальные направления естественных наук Химические науки Биологические науки Науки о Земле Космология Прикладные направления естественных наук Технические науки. Новая техника и прогрессивные технологии Область социально-гуманитарного знания и социальных отношений Косвенное Непосредственное Физические науки 4. Понятие метода и методологии. История возникновения научного метода Наука – разветвленная система достоверных и обобщенных знаний об окружающем мире Понятие метод (от греч. «методос» – путь к чему-либо) - совокупность приёмов и операций практического и теоретического освоения действительности Методология дословно означает «учение о методах», – целая область знаний, которая специально занимается изучением методов познания (изучая закономерности человеческой познавательной деятельности, вырабатывает на этой основе методы её осуществления) Этапы развития науки Древнейшие времена (до III-IV вв.н.э.)- «натуральная философия» Средние века (IV-XIII вв.) Эпоха возрождения (XIII-XVI вв.) Появление науки (XVI-XVII вв.) эксперимент – Г. Галилей, теоретическая наука – И. Ньютон Развитие научного метода: дифференциация наук (разделение наук на отдельные дисциплины) и интеграция наук (объединение наук) Фундаментальные вопросы, на которые отвечает натурфилософская картина мира: - о материи - о движении - о взаимодействии -о пространстве и времени - о причинности, закономерности и случайности - о космологии (общем устройстве и происхождении мира) Пример. Натурфилософская картина мира Аристотеля (геоцентризм) Научные картины мира: механическая (17 в.), электромагнитная (19 в.), неклассическая (1-я половина 20 в.), современная эволюционная Псевдонаука - имитация научной деятельности (астрология, уфология, парапсихология, биоэнергетика и т.п.) Отличительные признаки псевдонауки: - фрагментарность - некритический подход к исходным данным - невосприимчивость к критике - отсутствие общих законов - неверифицируемость и/или фальсифицируемость псевдонаучных данных 5. Классификация методов научного познания 5.1Эмпирические методы научного познания 1.Наблюдение (опосредованное и непосредственное) 2.Эксперимент (исследовательский или подтверждающий) 3.Измерение (прямые, косвенные) 1.Наблюдение есть чувственное (преимущественно визуальное) отражение предметов и явлений внешнего мира. Характерные черты научного наблюдения: целенаправленность активность планомерность 2. Научный эксперимент, более сложный метод эмпирического познания по сравнению с наблюдением, предполагает активное, целенаправленное и строго контролируемое воздействие исследователя на изучаемый объект для выявления и изучения тех или иных его сторон, свойств, связей. Экспериментатор может: 1. Преобразовывать исследуемый объект 2. Вмешиваться в естественное течение процессов 3. Создавать искусственные условия его изучения 4. Научный эксперимент должен являться воспроизводимым Исходя из методики проведения и получаемых результатов, эксперименты можно разделить на качественные и количественные. процесс, заключающийся в определении количественных значений тех или иных свойств, сторон изучаемого объекта, явления с помощью специальных технических устройств. В основе измерения лежит процесс сравнения объекта с единицей измерения, т.е. с эталоном. Пример. Системы единиц. СГС - сантиметр, грамм, секунда. СИ – метр, килограмм, секунда. 3. Измерение - Виды измерений. 1. Исходя из характера зависимости измеряемой величины от времени статические и динамические. 2. По способу получения результатов измерения - прямые и косвенные. Любые типы измерения содержат погрешность (теория погрешностей). Обычно рассчитываются абсолютная и относительная погрешности измерений. 5.2 Теоретические методы научного познания Абстрагирование заключается в мысленном отвлечении от каких-то (менее существенных) свойств, сторон, признаков изучаемого объекта с одновременным выделением, формированием одной или нескольких существенных сторон, свойств, признаков этого объекта. Идеализация представляет собой мысленное внесение определенных изменений в изучаемый объект в соответствии с целями исследования. Мысленный эксперимент предполагает оперирование идеализированным объектом, которое заключается в мысленном подборе тех или иных положений, ситуаций, позволяющих обнаружить какие-то важные особенности исследуемого объекта. Формализация – математическое описание различных объектов, явлений, основывающихся на соответствующих теориях. Формализация – язык науки. «Формулы» – это «слова» 5.3 Общенаучные методы научного познания Анализ – разделение объекта (мысленное или реальное) на составные части с целью отдельного их изучения. Синтез – соединение воедино отдельных частей (сторон, свойств, признаков и т. п.) изучаемого объекта, расчлененных в результате анализа, Аналогия – это подобие, сходство каких-то свойств, признаков или отношений у различных в целом объектов Моделирование: мысленное (идеальное); физическое; математическое (символическое или знаковое); численное (на ЭВМ), компьютерное. К мысленному моделированию относятся самые различные мысленные представления в форме тех или иных воображаемых моделей. Физическое моделирование характеризуется физическим подобием между моделью и оригиналом и имеет целью воспроизведение в модели процессов, свойственных оригиналу. Математическое и компьютерное моделирование связано с условно-знаковым представлением каких-то свойств объекта – оригинала. PS. Существуют и другие частнонаучные методы научного познания 6. Гуманитарные науки (науки об обществе и человеке) Основные отличия: субъективность знания, нестрогий образный язык, интерес к индивидуальным свойствам изучаемых предметов, сложность (или невозможность) верификации, фальсификации. 1. КИНЕМАТИКА 1.1 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ Кинематикой называют раздел механики, изучающий способы (не причины!) описания движений и связь между величинами, характеризующими эти движения. МОДЕЛИ МЕХАНИЧЕСКИХ СИСТЕМ: Материальная точка (МТ) – любой объект, формой и размерами которого в данной задаче (в данных условиях) можно пренебречь; Набор конечного числа материальных точек – достаточно общая модель произвольной механической системы. Абсолютно твёрдое тело (АТТ) – тело, форма и размеры которого при наличии тех воздействий, что описаны в условиях задачи, могут считаться неизменными. АТТ можно рассматривать как набор материальных точек с неизменными расстояниями между ними. Тело отсчёта, жёстко связанная с ним система координат и часы образуют систему отсчёта (СО). Y 0 X Z K Рис.1.1 О – начало координат (начало отсчёта); K – название системы отсчёта. Положение МТ в пространстве в определённый момент времени задаётся тремя её координатами (например, декартовыми,) или радиус-вектором : rx x , ry y , rz z . (1.1) При движении МТ её координаты становятся функциями времени: x x(t ) , y y (t ), z z (t ). (1.2 а, б, в) Аналогично, (1.3) r r (t ) . Закон движения МТ– правило, по которому можно определить её положение в любой момент времени. P.S. Закон движения (1.2 а, б, в) можно рассматривать как уравнения траектории, заданной в параметрическом виде (в роли параметра t). ОСНОВНЫЕ ВЕЛИЧИНЫ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ МТ (m) t1 т r (t1 ) Y (t1 ) l (t 1 ,t 2) т S (t , t t2 1 2) r (t 2 ) (t2 ) 0 X Z тр а ект ор ия K Рис.1.2 t r r (t1 ) – радиус-вектор в момент 1, (t2 ) – в момент t 2 , s (t1 , t2 ) – перемещение за промежуток времени (t1 , t 2 ) , l(t1 , t 2 ) – путь за (t1 , t 2 ) (длина отрезка траектории), (t1 ) – мгновенная скорость в момент времени t , 1 (t2 ) – мгновенная скорость в момент t . 2 PS. Векторы скорости (t1 ) и (t2 ) – касательные к траектории. Очевидно: s (t1 , t 2 ) r (t 2 ) r (t1 ) r . (1.4) При малых t t2 t1 очевидно, что s (t1, t2 ) l (t1, t2 ) . (1.5) Средняя скорость s (t1,t2 ) Δr υср(t1,t2 ) t2 t1 Δt . Мгновенная скорость r (t ) lim ср ( t, t t ) lim . t 0 t 0 t (1.6) (1.7 а) PS. Другой вид математической записи («точка» обозначает производную по времени) dr (t ) r . (1.7 б) dt Средняя путевая скорость l( t ,t ) l ср ( ) 1 2 , (1.8) t2 t1 t l l (t2 , t1 ) – путь, пройденный за t t2 t1. При t 0 получаем: Мгновенная путевая скорость (при t Или 0 ): l . t 0 t dl ( ) . dt (1.9) ( ) lim (1.10) Из (1.5), (1.6), (1.7а), (1.8) и (1.9), следует, чтомгновенная путевая скорость совпадает с модулем вектора мгновенной скорости (подумать!): () . (1.11) Среднее ускорение за промежуток времени (t1 , t 2 ) υ (t 2 )-υ (t1 ) aср (t1 ,t 2 ) . t 2 -t1 t Мгновенное ускорение (в момент t ) : d . a (t ) dt Очевидно: d 2 r . ar 2 dt : (1.12) (1.13) (1.14) r PS.1 Если закон движения задан, например, известна зависимость (t ) , то мы имеем о движении полную информацию, и все величины, определённые равенствами (1.6) – (1.14) легко вычисляются, точно так же, как и их проекции на декартовы оси. r (t ) (t ) PS.2 Переход и выполняется с помощью (t ) a (t ) дифференцирования. r (t ) , a (t ) (t ) выполняется с помощью интегрирования. Обратно: (t ) r0 r (0); Чтобы найти r (t ) по заданной (t ) ,t необходимо начальное значение t (1.15) r (t ) r (0) (t ' )dt ' r0 (t ' )dt ' . 0 0 Аналогично: t t (t ) (0) a (t ' )dt ' 0 a (t ' )dt '. (1.16) 0 0 Пример 1. Пусть МТ движется с a const. Тогда с помощью (1.16) можно найти (1.17) 0 at . Интегрируя ещё раз, получаем закон движения: at 2 . (1.18) r (t ) r0 0t 2 Это равенства, связывающие кинематические величины в общем случае, т.е. при произвольном движении МТ. Пример 2. (из школьной жизни!). Прямолинейное равноускоренное движение. 2as 2 0 2 ; s 0t at 2 2; 0 at ; Очевидно, что s(t ); a (t ) s(t ). a const. (1.19) Векторные равенства можно записать в проекциях на оси координат: , (1.20а,б) x , dx ( x )ср x t dt d x x a ( a x )ср x (1.21а,б) dt , t , t x( t ) x0 x ( t )dt , (1.22) 0 t x ( t ) 0 x ax ( t )dt 0 и т.д. (1.23) 1.2. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ: ТАНГЕНЦИАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ. d a (t ) . dt Итак Очевидно, при криволинейном движении ускорение материальной точки отлично от нуля, т.к. вектор скорости изменяется по величине и по направлению. Представим вектор скорости МТ в виде (1.24) 1 где . (1.25) т.е. – единичный вектор, направленный по скорости Продифференцируем уравнение (1.24),: Обозначим: . d d d a dt dt dt . (1.26) d a dt , (1.27) d an dt . (1.28) Тогда: (1.29) a a an . Первое слагаемое в (1.29) a – касательное или тангенциальное ускорение: d 0 , (1.30а) a при dt при d 0 . (1.30б) a dt Второе слагаемое - an называется нормальной составляющей, она нормальна, т.е. перпендикулярна, к вектору скорости (см. ниже!). (t dt ) (t dt ) (t ) (t ) Рис.1.3 (t dt ) d d (t ) . d Рис.1.4 Можно считать: d (t ). (1.31) Рассматривая этот треугольник как бесконечно малый сектор, имеем d d . (1.32) d d . (1.33) Но 1 . Отсюда Если ввести бесконечно малый вектор поворота d , направление которого указано на рисунке 1.4 – «к нам», – то будем иметь с учётом (1.31) и (1.33): (1.34) d d , Таким образом, (см. (1.31), (1.28)), an (1.35) Следовательно, равенство (1.29) – разложение вектора ускорения на две взаимно перпендикулярные составляющие. Далее, an можно представить в виде d d an , , dt dt Направления a , a n , a в случае d dt 0 показаны на рисунке 1.5. a an . Рис.1.5 (1.36) a Если считать малый отрезок криволинейной траектории частью окружности, то величина d (1.37) dt называется вектором угловой скорости. Вектор определяет как направление поворота, так и величину угла поворота радиуса-вектора за единицу времени. Направление движения МТ по окружности и направление связаны правилом буравчика. 1.3 НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ. СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ. РАДИУС КРИВИЗНЫ ПЛОСКОЙ ТРАЕКТОРИИ. r (t dt ) O . d d r (t ) dr Рис.1.6 Рассмотрим окружность радиуса r , по которой движется материальная точка (рис.1.6). ( t ) const PS. . При движении против часовой стрелки направлена «к нам», по часовой – «от нас». r d r r За время dt радиус-вектор изменится на : от значения (t ) до значения r (t dt ) . Используя аналогию треугольников, построенных из векторов, которые показаны на рис. 1.4 и 1.6, нетрудно получить равенство, аналогичное соотношению (1.34): (1.40) dr d , r . Поделив обе части (1.40) на dt , будем иметь , r . (1.41) Дифференцируя (1.41), находим ускорение: d (1.42) a , r , dt Второе слагаемое в (1.42) ( см. (1.36) ) есть нормальное ускорение: Тогда первое, очевидно, равно a : , an . (1.43) d . (1.44) a ,r dt Введём новое определение: угловым ускорением МТ назовём величину d . dt (1.45) Теперь ускорение её запишется с учётом (1.41) в виде a , r , r . (1.46) Двойное векторное произведение в (1.46) вычислим по известной математической формуле , a b ,c b ( a ,c ) c ( a ,b ) (1.47) ,r ,r r , . (1.48) что даёт Учитывая, что r, получаем: , r 2r . (1.49) Таким образом, в разложении (1.29) a a an слагаемые имеют вид: a , r , a n 2 r . (1.50 а,б) Очевидно, нормальная составляющая ускорения – это хорошо известно из школьного курса центростремительное ускорение. Ускорение материальной точки , движущейся по окружности, называют также полным ускорением. Рассмотрим аналогию между ускоренными прямолинейным и криволинейным движениями (на примере МТ, движущейся по окружности). e r Y . OZ X Рис.1.7 e Ось OZ направлена «к нам», – единичный вектор, указывающий направление отсчёта положительных углов, которое связано с направлением OZ правилом буравчика Для движения вдоль оси OX имеем dx x dt . d x d 2 x ax 2 dt dt (1.51а, б) Для движения по окружности: d dt z d z d 2 z . 2 dt dt (1.52а, б) Равнопеременное движение вдоль оси описывается равенствами: ax const , (1.53 а) (1.53 б) x 0 x axt , axt 2 x x0 0 xt 2 , (1.53 в) axt 2 x 0 xt 2 . (1.53 г) Равнопеременное движение по окружности: z const , z 0 z zt , 0 0 zt zt 2 0 z t , (1.54 а) (1.54 б) (1.54 в) 2 zt 2 , 2 где – угловое перемещение материальной точки. (1.54 г) Таблица соответствия линейных и угловых величин линейные dr a x x ax угловые d z z Уравнения, связывающие линейные и угловые переменные, характеризующие движение МТ по окружности ( r R) : , (1.55а, б) d r d R ; dr d , r (1.56а, б, в) z R ; , r , a R R a , r , (1.57а, б, в) a z R ; Здесь , a – проекции скорости и ускорения на вектор e , , a a 2 (1.58 а, б) ; 2 2 a n r an R , . (1.59 а, б) R Малую окрестность точки плоской криволинейной траектории материальной точки можно рассматривать как малую дугу некоторой окружности. Радиус этой окружности – радиус кривизны траектории в окрестности данной точки, Rкр . Эта величина удовлетворяет равенству аналогичному (1.59 б). an 2 Rкр . (1.60)