Кинетика диффузионно-контролируемых реакций

Лекция 2
Кинетика диффузионноконтролируемых реакций
Воробьев А.Х.
2012
Диффузионное приближение
Δm
Поток: j 
St
C
Уравнение Фика: j   D
x
Коэффициент диффузии
C
X
1
1l2 1 2
D  lv 
 v 
3
3  3
2
l
D
6
Формула Стокса-Эйнштейна:
ν
j  (n1  n 2 )
6
kT
D  UkT 
6 R
Методы определения
Интегральные:
Истечение из капилляра.
Полярография.
Измерение профиля.
Томография.
Восстановление флуореесценции
после фотообесцвечивания
Метод Тейлора
Четырехкомпонентная смесь
Кросс-диффузия
 Ci
 Ck
ji   Dii
  Dik
x k
x
Три механизма:
- электростатическое взаимодействие;
- исключенный объем;
- комплексообразование.
Коэффициент диффузии
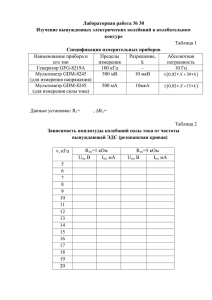
t, (C) D, м2/с
В воде
t, (C)
D, м2/с
He, 1 атм
0
1,6210-4
C2H5OH
20
1,2410-9
N2, 1 атм
0
1,710-5
C 6H 6
20
1,0210-9
н-Гексан
25
4,2110-9
Глицерин
15
0,7210-9
C 6H 6
25
2,1510-9
Глюкоза
11
0,5210-9
C2H5OH
25
1,0510-9
Сахароза
11
0,3610-9
CCl4
25
1,4110-9
H+
25
9,3110-9
H 2O
25
2,4310-9
K+
25
1,9610-9
O2 в ПЭ
25
4,610-11
Ag+
25
1,6510-9
C3H8 в ПЭ
25
3,210-12
Ca2+
25
7,9210-10
[Fe(CN)6]4-
25
7,3610-10
Уравнение диффузии
 C (r )
 div[ D(r ) grad (C (r ) )]  f (r , t , C )
t
C
 2 C  2C  2C
 DC  f (r , t )  D( 2 
 2 )  f ( x, y, z, t )
2
t
x y z
2


1


1

r 2 
(r 2 ) 
(sin  )  2
r
 r sin  
 sin   2
C
 C
 D 2  f ( x, t , C )
t
x
2
 T   2T

 q(x,t , T)
2
 t c x
Стационарная диффузионная
задача
C (0)  C0 /(1  k s / D)
C (0)  C0 /(1  k s / D)
 2C
x 2
0
Граничные условия:
1)
C( )  C 0
dC
2) D( ) x  0  k s C(0)
dx
Решение:
C0
D x
C( x ) 
(
 )
D
k  
1 s
k s
C (0)  C0 /(1  k s / D)
w  ks /(1  k s / D)
Нелинейное уравнение
C
Задача о диффузии
реагента
C
d 2C
D
 kC n
t
dx 2
C( x 0 )  C 0
C0
0D
x
-x0
0
nC  Prod
d 2C
dx
x0
2
 kC
n
Понижение степени:
Неполное решение:
p
dC
2k

[C n 1  C(0) n 1 ]1 / 2
dx
(n  1) D
Скорость реакции:
dp
Dp
 kC n  0
dC
dC
( ) x 0  0
dx
dC
p
dx
( n 1) / 2
2k
 dC 
w   

C0
(n  1) D
 dx  x  x 0
Искусственная стационарность
B
A
r0
R = rA+rB
D=DA+DB.
Задача о клеточном эффекте
W
 2 W 2 W
 D(

)
2
t
r r
r
w  rW
w
 2w
D
0
2
t
r
W(r)
Ответ:
R
PR 
D
r0 (
 1)
ksR
r
R
r0
Нестационарная кинетика
С
 С 2 С
 D(

)
2
t
r r
r
2
w  rС
t1
C
t2
t3
2
w
 w
D
t
r 2
0
r2
C
exp(
)
3/ 2
4 Dt
(4 Dt )
N
x  2Dt
r
Методы решения
Преобразование Лапласа
F(s)

f(t)
F(s)   f ( t )e  st dt
0
Разделение переменных:
C ( x, t )  P( x)Q(t )
1 Q
1  2P

D 2 Q (t )  t P ( x)  x 2
1
Недостаток: применимы к линейным уравнениям!
Задача Смолуховского
2
w
 w
D
2
t
r
R = rA+rB
D=DA+DB.
w  rW
Граничные условия:
1) W (r,0)  W0
2) W(R , t )  0
3) W (, t )  W0
Решение:
R
rR
W(r, t )  W0 [1  erfc(
)]
r
2 Dt
w r  4RD(1 
R
Dt
)[A][B]
1
W t=0
t1
t2
t3
r
R
Константа скорости реакции
R
kr  4 RD(1 
)  4 RD
 Dt
D
kT
6 R
2kT
kr 
3
Нестационарная часть
кинетики
2
R
t
D
Диффузия-реакция
Структуры в реакции
Белоусова-Жаботинского
Два коэффициента
диффузии, константа
скорости реакции
Смещение при диффузии
x
Dt
Нормальная (Гауссова) диффузия
x
1

t ; <
2
Аномальная (странная) диффузия
медленная (заторможенная)
subdiffusion
x
1

t ;
2
Аномальная (странная) диффузия
быстрая (ускоренная)
superdiffusion
Полимеры
Пористые материалы
Потоки жидкости
Геологические породы и т.д.
Неоднородность среды
Теория перколяция (протекания)
Фрактальная размерность
Размерность по Хаусдорфу
ln[N()]
d  lim{
}
 ln[1/ ]
Салфетка Серпиннского
Самоподобие при увеличении
разрешения:
Фрактальные блуждания
Диффузионные скачки на
различные расстояния.
Модель подвижного
свободного объема.
10
20
30
40
P{R  r}  r  , r  
P{  t}  t  , r  
 - память среды
Обобщенное уравнение
диффузии

  
 p(x, t)
 D   2 

t
 x 
2
/2
t 
p(x, t) 
(x)
(1  )
0    2, 0    1
где производная дробного порядка:


t
 p(x, t)
t
 p(x,t)d




(t

)
(1  ) t 0
t
Диффузия взаимодействующих
частиц
C
 div( j )  0
t
C
j  D( gradC 
gradV )
kT
q1q 2
R on 
kT
Туннельная реакция
P(r )  P0 exp( r )
Диполь-дипольное
взаимодействие
P (r )  P0 / r
C0
6
r
R
x
Dt
k  4 DR eff
(R e ff  R) 2
D
Rd
 exp( R e ff )
Вращательная подвижность
Газовая фаза (моменты инерции, вращательная энергия).
Твердая фаза (либрации).
U0
/2
Жидкая фаза
 r < t ; k r =4πRDt
 r   t ; kr  4 RDt S 2

Вращательная диффузия

1  2 
1 

1  2
 Dt 2
(r
)  Dr
(sin  )  2
t
r r
r
sin  
 sin   2
 Yl m ( ,  )
1 
1  2Yl m ( ,  )
m
(sin 
) 2


l
(
l

1)
Y
l ( ,  )
2
sin  

sin 

Методы измерения:
- поляризация флуоресценции;
- ЭПР спектроскопия;
- ЯМР спектроскопия;
- релаксация дихроизма (двулучепреломления)
Коэффициент вращательной
диффузии
kT
Dr 
3
6 R
Reff = 3.8A (пропанол),
2.9A (кумол),
1.8A (omim BF4)
Rgeom ~ 5.5 A
Заключение
1. Решаются линейные диффузионные задачи.
2. Осложнения – нелинейность, кросс-диффузия
(неидеальность среды)
3. Реальные жидкости, полимеры, адсорбенты.....ФРАКТАЛЫ
4. Диффузия – фрактальное движение
и/или движение по фракталу
5. Диффузия взаимодействующих частиц – эмпирически
6. Реакция-диффузия – нелинейная задача