С3 – поиск выигрышной стратегии
реклама
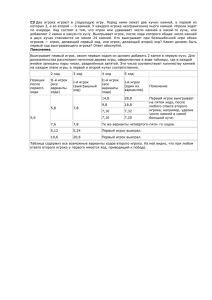
С3 – поиск выигрышной стратегии Два игрока играют в следующую игру. Имеются три кучи камней, содержащих соответственно 2, 3, 4 камня. За один ход разрешается или удвоить количество камней в какой–нибудь кучке, или добавить по два камня в каждую из куч. Предполагается, что у каждого имеется неограниченный запас камней. Выиграет тот игрок, после чьего хода в какой-нибудь кучке становится не меньше 15 или во всех трех кучах суммарно становится не меньше 25 камней. Игроки ходят по очереди. Выясните, кто выигрывает при правильной игре, — первый или второй игрок. Решение: 1 ход 2 ход 3 ход Стартовая 1-ый игрок 2-й игрок анализ уже рассчитанных состояний игры. позиция (все (все варианты варианты хода) хода) 8,3,4 4,3,4 4,6,4 4,3,8 6,5,6 Выигрыш 1-го игрока Проигрыш 1-го игрока продолжении Выигрыш 1-го игрока при любом Проигрыш 1-го игрока при любом продолжении 2,12,4 Выигрыш 1-го игрока 2,6,4 2,3,4 2,6,8 Выигрыш 1-го игрока 4,6,8 Выигрыш 1-го игрока 2,3,8 Проигрыш 1-го игрока (при ходе второго 2,3,16) 8,5,6 Выигрыш 1-го игрока 4,10,6 Выигрыш 1-го игрока 4,5,6 4,5,12 Выигрыш 1-го игрока 6,7,8 Выигрыш 1-го игрока Из таблицы очевидно, что при правильно выбранной стратегии (первый ход должен быть 2,3,4 - 4,5,6).выигрывает 1-й игрок. Допущенные ошибки: Рассмотрены не все возможные варианты ходов игроков Лучше оформлять дерево игры не в обычном, а табличном виде. 4,6,4 Тренировочные задания в формате ЕГЭ: 1. Два игрока играют в следующую игру. На координатной плоскостистоит фишка. В начале игры фишка находится в точке с координатами (0,2). Игроки ходят по очереди. Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трех точек: (x-1,y+4), (x+2,y+3), (x+3,y-1). Игра заканчивается, как только расстояние по прямой от фишки до начала координат станет не меньше 10. Выигрывает игрок, который сделал последний ход. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте. 2. Два игрока играют в следующую игру. На координатной плоскости стоит фишка. В начале игры фишка находится в точке с координатами (-2,-1). Игроки ходят по очереди. Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трех точек: (x-1,y+4), (x+2,y+3), (x+3,y-1). Игра заканчивается, как только расстояние по прямой от фишки до начала координат станет не меньше 10. Выигрывает игрок, который сделал последний ход. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте. 3. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 2, а во второй 7 камней. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в какой-то куче или добавляет 3 камня в какую-то кучу. Игрок, после хода которого общее число камней в двух кучах становится больше 20, проигрывает. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте. 4. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в каждой из которых лежит по три камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в какой-то куче или добавляет 3 камня в какую-то кучу. Игрок, после хода которого общее число камней в двух кучах становится больше 20, проигрывает. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.