Применение производной 1. Максимумом функции на отрезке

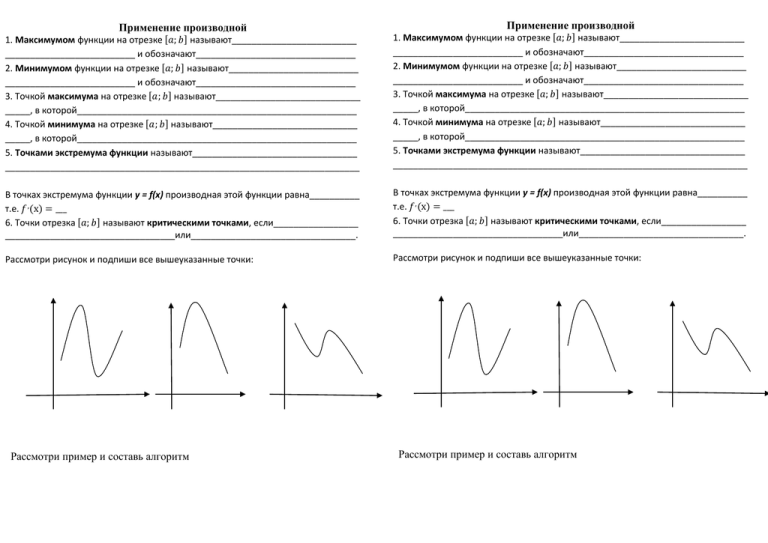
Применение производной
Применение производной
1. Максимумом функции на отрезке [𝑎; 𝑏] называют_________________________
__________________________ и обозначают________________________________
2. Минимумом функции на отрезке [𝑎; 𝑏] называют__________________________
__________________________ и обозначают________________________________
3. Точкой максимума на отрезке [𝑎; 𝑏] называют_____________________________
_____, в которой________________________________________________________
4. Точкой минимума на отрезке [𝑎; 𝑏] называют_____________________________
_____, в которой________________________________________________________
5. Точками экстремума функции называют_________________________________
_______________________________________________________________________
1. Максимумом функции на отрезке [𝑎; 𝑏] называют_________________________
__________________________ и обозначают________________________________
2. Минимумом функции на отрезке [𝑎; 𝑏] называют__________________________
__________________________ и обозначают________________________________
3. Точкой максимума на отрезке [𝑎; 𝑏] называют_____________________________
_____, в которой________________________________________________________
4. Точкой минимума на отрезке [𝑎; 𝑏] называют_____________________________
_____, в которой________________________________________________________
5. Точками экстремума функции называют_________________________________
_______________________________________________________________________
В точках экстремума функции y = f(x) производная этой функции равна__________
т.е. 𝑓 , (х) = ___
6. Точки отрезка [𝑎; 𝑏] называют критическими точками, если_________________
__________________________________или_________________________________.
В точках экстремума функции y = f(x) производная этой функции равна__________
т.е. 𝑓 , (х) = ___
6. Точки отрезка [𝑎; 𝑏] называют критическими точками, если_________________
__________________________________или_________________________________.
Рассмотри рисунок и подпиши все вышеуказанные точки:
Рассмотри рисунок и подпиши все вышеуказанные точки:
Рассмотри пример и составь алгоритм
Рассмотри пример и составь алгоритм
Алгоритм нахождения наибольшего и наименьшего значений функции
на отрезке:
Этапы
1. Найти
2. Прировнять производную к
найти
взять те, которые
данному отрезку.
3. Вычислить
функции в,
точках и на
отрезка.
4. Из
выбрать
и
,
значений
Пример: для функции
f(х) = 2х3 – 3х2 – 36х + 5 на 0;4
1) f′(x) = 6х2 – 6х - 36
2) 6х2 – 6х – 36 = 0
х = -2, х = 3
Отрезку 0;4 принадлежит только: х
=3
3) f(0) = 5
f(3) = -76
f(4) = -59
max f(x)  f(0)  5
0;4
min f(x)  f(3)  76
0;4
Уравнение касательной
Геометрический смысл производной:
Уравнение касательной: y =
Чтобы составить уравнение касательной надо:
1. Найти
2. Найти
3. Найти
4. Написать уравнение касательной у =
Механический смысл производной
Алгоритм нахождения наибольшего и наименьшего значений функции
на отрезке:
Этапы
1. Найти
2. Прировнять производную к
найти
взять те, которые
данному отрезку.
3. Вычислить
функции в,
точках и на
отрезка.
4. Из
выбрать
и
,
значений
Пример: для функции
f(х) = 2х3 – 3х2 – 36х + 5 на 0;4
1) f′(x) = 6х2 – 6х - 36
2) 6х2 – 6х – 36 = 0
х = -2, х = 3
Отрезку 0;4 принадлежит только: х
=3
3) f(0) = 5
f(3) = -76
f(4) = -59
max f(x)  f(0)  5
0;4
min f(x)  f(3)  76
0;4
Уравнение касательной
Геометрический смысл производной:
Уравнение касательной: y =
Чтобы составить уравнение касательной надо:
1. Найти
2. Найти
3. Найти
4. Написать уравнение касательной у =
Механический смысл производной
Механический смысл производной
Алгоритм исследования функции на максимум и минимум.
Алгоритм исследования функции на максимум и минимум.
Признак максимума функции. Если функция f ____________________ в точке х0,
а ________
на интервале (а, х0) и _____________ на интервале (х0, в) , то точка
х0 является _________________________________________ функции f .
Признак минимума функции. Если функция f ____________________ в точке х0 ,
а ________
на интервале (а, х0) и _____________ на интервале (х0, в) , то точка
х0 является _________________________________________ функции f .
Признак максимума функции. Если функция f ____________________ в точке х0,
а ________
на интервале (а, х0) и _____________ на интервале (х0, в) , то точка
х0 является _________________________________________ функции f .
Признак минимума функции. Если функция f ____________________ в точке х0 ,
а ________
на интервале (а, х0) и _____________ на интервале (х0, в) , то точка
х0 является _________________________________________ функции f .
1.Найти _____________________________________________ функции.
2.Найти ____________________________________________________
3.Найти ____________________, в которых производная______________ т.е.
4.Найти точки, в которых производная не существует.
5.Исследовать знак _____________________________________ в промежутках.
Если в точке х0 производная меняет знак с ____ на ____, то х0 Если в точке х0 производная меняет знак с ____ на ____ , то х 0-
1.Найти _____________________________________________ функции.
2.Найти ____________________________________________________
3.Найти ____________________, в которых производная______________ т.е.
4.Найти точки, в которых производная не существует.
5.Исследовать знак _____________________________________ в промежутках.
Если в точке х0 производная меняет знак с ____ на ____, то х0 Если в точке х0 производная меняет знак с ____ на ____ , то х 0-
Приведите пример:
Приведите пример:
Исследование функции на возрастание и убывание.
Исследование функции на возрастание и убывание.
Достаточный признак возрастания функции. Если ___________ в каждой точке
интервала I , то функция f ________________________________________ на I.
Достаточный признак убывания функции. Если _____________в каждой точке
интервала I , то функция f ________________________________________ на I.
Алгоритм исследования функции на возрастание и убывание функции.
1.Найти
2.Найти
3.Найти промежутки, в которых _______________________ больше _______
т.е. ______
и __________________________________ т.е. _________
3.Исследовать знак _______________________в полученных промежутках т.е.
если: ____________ ,то функция ____________________ и если_____________,
то функция __________________________.
Достаточный признак возрастания функции. Если ___________ в каждой точке
интервала I , то функция f ________________________________________ на I.
Достаточный признак убывания функции. Если _____________в каждой точке
интервала I , то функция f ________________________________________ на I.
Алгоритм исследования функции на возрастание и убывание функции.
1.Найти
2.Найти
3.Найти промежутки, в которых _______________________ больше _______
т.е. ______
и __________________________________ т.е. _________
3.Исследовать знак _______________________в полученных промежутках т.е.
если: ____________ ,то функция ____________________ и если_____________,
то функция __________________________.
Приведите пример:
Приведите пример: