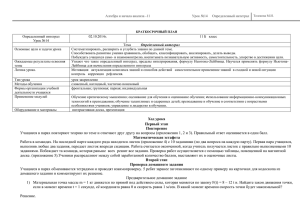
Случай поверхности, заданной как график явной функции z=φ(x,y)

Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ
3 семестр
Лекция 5
Поверхностные интегралы.
09 октября 2014 года
Лектор: Профессор НИЯУ МИФИ, д.ф.-м.н.
Орловский Дмитрий Германович
Поверхностный интеграл 1 рода
v
Ω
u
 x  x (u, v )
 y  y (u, v )


 z  z (u, v )
(u, v )  
z
S
y
x
Разбиение поверхности:
T  {1, 2 ,..., n }  U  {S1, S2 ,..., Sn}
Характеристика разбиения:
 (U )  Max Sup  ( x, y )
1i n x , yS
i
Поверхностный интеграл 1 рода
Пусть на поверхности S задана числовая функция f(x,y,z). На
каждом участке поверхноcти Si выбираем по точке ξi и составляем
интегральную сумму
n
S ( f ,U )   f (ξ i ) | Si |
i 1
(| Si |  площадь участка поверхности Si )

S
f ( x, y , z )dS  lim S ( f ,U )
 (U )0
Поверхностный интеграл 1 рода
(1)
 dS | S |
(| S |  площадь поверхности S )
S
(2)
 ( f ( x, y, z )   g ( x, y, z ))dS    f ( x, y, z )dS    g ( x, y, z )dS
S
(3)
S
f g 
 f ( x, y, z )dS   g ( x, y, z )dS
S
(4)
|  f ( x, y, z )dS |   | f ( x, y, z ) | dS
S
(5)
S
S
Если U  {S1 , S2 ,..., Sn }  разбиение S , то
n
 f ( x, y, z )dS    f ( x, y, z )dS
S
i 1 Si
S
Поверхностный интеграл 1 рода
Формулу для вычисления поверхностного интеграла 1 рода
приведем без доказательства. Здесь будем использовать следующие
обозначения
 x y z 
ru   , ,  ,
 u u u 
 x y z 
rv   , ,  ,
 v v v 
E | ru |2 , G | rv |2 , F  ( ru , rv ).
Элемент площади поверхности
dS | ru  rv | dudv  EG  F 2 dudv.
 f ( x, y, z )dS   f ( x(u, v ), y (u, v ), z(u, v ))dS
S

Поверхностный интеграл 1 рода
N  ru  rv
Поверхностный интеграл 1 рода
Случай поверхности, заданной как график явной функции z=φ(x,y)
x  u
y  v


 z   ( u, v )
(u, v )  
z   ( x, y )
S

 f ( x, y, z)dS  
S

ru  1,0,  / x,
rv  0,1,  / y,
E  1  ( / x )2 ,
G  1  ( / y ) 2 ,
F  ( / x )( / y ),
EG  F 2  1  ( / x)2  ( / y )2 .
2
     
f ( x, y,  ( x, y )) 1  
dxdy
 

 x   y 
2
Поверхностный интеграл 1 рода
Пример. Вычислить
 zdS ,
S
где S – поверхность геликоида
ru  {cos v,sin v,0},
rv  {u sin v, u cos v,1}
 x  u cos v
 y  u sin v


z  v
(0  u  a,0  v  2 )
ru  rv  {sin v,  cos v, u}
dS | ru  rv | dudv  1  u 2 dudv
Поверхностный интеграл 1 рода
 zdS 
S

0 u  a
0 v  2 
a
2
0
0
v 1  u 2 dudv   1  u 2 du  vdv 
a
2 2
1
u
 v

1  u 2  ln(u  1  u 2 )  
2
2
0 2


  2 a 1  a 2  ln a  1  a 2
Ответ:




0
2
2
2
zdS


a
1

a

ln
a

1

a

S

Поверхностный интеграл 1 рода
Пример. Вычислить
 ( x  y  z )dS ,
S
где S - поверхность
x 2  y 2  z 2  a 2 , z  0 (a  0).
z
z   ( x, y )  a 2  x 2  y 2
S
y
a
x
a
  {( x, y ) : x 2  y 2  a 2}
Поверхностный интеграл 1 рода
Элемент площади поверхности:
 ( x, y )  a 2  x 2  y 2 ,

x

y

,

x
y
a2  x2  y2
a2  x2  y2
2
adxdy
     
dS  1  
dxdy 
 

 x   y 
a2  x2  y2
2
Искомый интеграл
I   ( x  y  z )dS 
S
 ( x  y 
x 2  y 2 a 2
a x y
2
2
2
)
adxdy
a x y
2
2
2

Поверхностный интеграл 1 рода
a
xdxdy

a x y
2
x 2  y 2 a 2
2
2
a
ydxdy

a x y
2
x 2  y 2 a 2
2

a
2
dxdy.
x 2  y 2 a 2
Далее вычисляем каждый из интегралов отдельно, переходя
в полярные координаты
 x  r cos 

 y  r sin 
(1)

x 2  y 2 a 2
(2)

x 2  y 2 a 2
2
xdxdy
a x y
2
2
2
ydxdy
a x y
2
2
2
2
a


a
 d 
0
0
2
a
 d 
0
0
2
r cos 
a r
2
2
a r
 cos d 
0
2
r sin 
2
rdr 
2
a2
(3)  dxdy   d  rdr  2
  a2
2
0
0
x 2  y 2 a 2
rdr 
a
0
a
 sin  d 
0
0
r 2dr
a r
2
2
r 2dr
a r
2
I  a
2
3
0
0
Поверхностный интеграл 1 рода
Пример. Вычислить
I   ( x 2  y 2 )dS ,
S
x 2  y 2  z  1.
где S – граница тела
z
S  S1
z 1
z  x2  y2
y
1
1
x
  {( x, y ) : x 2  y 2  1}
S2
S1 – боковая поверхность конуса
S2 – основание конуса
I   ( x 2  y 2 )dS   ( x 2  y 2 )dS
S1
S2
Поверхностный интеграл 1 рода
Поверхность S1 является графиком функции z  x 2  y 2 .

x
2
2
dS  1  z x  z y dxdy  1  
 x2  y2

z 1
z
2

 dxdy  2dxdy


I1   ( x 2  y 2 )dS  2  ( x 2  y 2 )dxdy
S2

S1
z x y
2
S1
2
 
y
  2
  x  y2
 
2
y
I 2   ( x 2  y 2 )dS   ( x 2  y 2 )dxdy

S2
1
1
x
  {( x, y ) : x 2  y 2  1}
I  ( 2  1)

x  y 2 1
2
( x 2  y 2 )dxdy
Поверхностный интеграл 1 рода
I  ( 2  1)

( x 2  y 2 )dxdy
x 2  y 2 1
Полученный интеграл вычисляем в полярных координатах
2
1
0
0
I  ( 2  1)  d  r 3dr  ( 2  1)  (2 ) 
Ответ:
I
 ( 2  1)
2
1  ( 2  1)

4
2
Поверхностный интеграл 2 рода
v
Ω
u
 x y z 
ru   , ,  ,
 u u u 
 x  x (u, v )
 y  y (u, v )


 z  z (u, v )
(u, v )  
 x y z 
rv   , ,  ,
 v v v 
Первая ориентация
n1  ru  rv
z
S
y
x
Вторая ориентация
n2  rv  ru
Первая ориентация поверхности считается согласованной с
положительной ориентацией плоскости uOv, а вторая – с
отрицательной.
Поверхностный интеграл 2 рода
Лист Мебиуса
Август Фердинанд Мёбиус (1790-1868) – ученик «короля» математиков
Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие
другие, кому математика обязана своим развитием. В те времена
занятия математикой не встречали поддержки, а астрономия давала
достаточно денег, чтобы не думать о них, и оставляла время для
собственных размышлений. И Мёбиус стал одним из крупнейших
геометров XIX века.
В возрасте 68 лет Мёбиусу удалось сделать открытие поразительной
красоты. Это открытие односторонних поверхностей, одна из которых –
лист Мёбиуса (или лента). Мёбиус придумал ленту, когда наблюдал за
горничной, неправильно одевшей на шею свой платок.
Для изготовления листа Мёбиуса нужно взять бумажную полоску –
длинный узкий прямоугольник АВСD (удобные размеры: длина 30 см,
ширина 3 см). Перекрутив один конец полоски на 180º, склейте из нее
кольцо (точки А и С, В и D).
Поверхностный интеграл 2 рода
Лист Мебиуса
Журнал
“Квант”
Эмблема мехмата МГУ (http://www.math.msu.ru/)
Поверхностный интеграл 2 рода
Лист Мёбиуса служил вдохновением
для скульптур и для графического
искусства. Эшер был одним из
художников, кто особенно любил его.
Эшер посвятил несколько своих
литографий этому математическому
объекту. Одна из известных — лист
Мебиуса II, показывает муравьёв,
ползающих по поверхности ленты
Мёбиуса.
Поверхностный интеграл 2 рода
Прага
Поверхностный интеграл 2 рода
Нахимовский проспект 45
Москва, Комсомольский
проспект, 21/10,
кинотеатр "Горизонт"
Поверхностный интеграл 2 рода
Скамейка в Киеве
Лондон. Гагарин, стоящий
на ленте Мебиуса.
Лента Мебиуса в Екатеринбурге
Музей истории и техники в Вашингтоне
Поверхностный интеграл 2 рода
В рассказе «Лист Мебиуса» автора А. Дж. Дейча, бостонское
метро строит новую линию, маршрут которой становится настолько
запутанным, что превращается в ленту Мёбиуса, после чего на этой
линии начинают исчезать поезда (http://lib.ru/RAZNOE/subway.txt)
По мотивам рассказа было снято несколько фильмов:
1988 (СССР, режиссер Леонид Партигул) “Лист Мебиуса”,
1993 (Германия, режиссер Матти Гешоннек) “Мебиус”,
1996 (Аргентина, режиссер Густаво Москера) “Мебиус”,
2005 (Германия, режиссер Джо Пройслер) “Мебиус 17”.
фильм Партигула: http://www.youtube.com/watch?v=AuJockV3KVg
http://www.youtube.com/watch?v=m5iYfaZ3BU0
фильм Гешоннека: http://kinofilms.tv/film/myobius/53931/
фильм Москера: http://1kinotv.ru/prikliuchenia/9632-mebius-1996.html
фильм Пройслера: http://kinozon.tv/65163
Поверхностный интеграл 2 рода
Существуют технические применения ленты Мёбиуса. Полоса
ленточного конвейера выполняется в виде ленты Мёбиуса, что
позволяет ему работать дольше, потому что вся поверхность ленты
изнашивается равномерно. Также в системах записи на
непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить
время записи). Во многих матричных принтерах красящая лента
также имеет вид листа Мёбиуса для увеличения её ресурса.
Устройство под названием резистор Мебиуса — это недавно
изобретенный
электронный элемент, который
не имеет
собственной индуктивности.
Есть гипотеза, что спираль ДНК сама по себе тоже является
фрагментом ленты Мебиуса и только поэтому генетический код так
сложен для расшифровки и восприятия. Больше того – такая
структура вполне логично объясняет причину наступления
биологической смерти – спираль замыкается сама на себя и
происходит самоуничтожение.
Поверхностный интеграл 2 рода
n
a
(поле нормалей)
(заданное векторное поле)
a  {P, Q , R}
S
Определение.
Нормальная компонента векторного поля – это проекция векторного
поля на поле нормалей
(a , n )
an 
|n |
 adS   Pdydz  Qdzdx  Rdxdy   a dS
n
S
S
S
Поверхностный интеграл 2 рода
a  {P, Q , R}
Пусть
,  , 
углы, которые образует нормаль
с осями координат, тогда
S
an  P cos   Q cos   R cos  .
Поэтому
 adS   ( P cos   Q cos   R cos  )dS
S
S
Поверхностный интеграл 2 рода
(1)
 ( a   b )dS    adS    bdS
S
(2)
S
 adS    adS
S 1
(S-1 – это та же поверхность S, но
ориентированная противоположно)
S
(3) Для любого разбиения
S
U  {S1 , S2 ,..., Sn },
n
 adS    adS
i 1
S
Si
(4) Если векторное поле перпендикулярно нормали, то
 adS  0
S
Поверхностный интеграл 2 рода
(5) Любое векторное поле можно представить следующим образом
a  {P, Q, R}  {P,0,0}  {0, Q,0}  {0,0, R}
поэтому
 adS   Pdydz  Qdzdx  Rdxdy 
S
S
  Pdydz   Qdzdx   Rdxdy
S
S
S
Поверхностный интеграл 2 рода
Формулы для вычисления
v
 x  x (u, v )
 y  y (u, v )


 z  z (u, v )
(u, v )  
Ω
u
 x y z 
ru   , , 
 u u u 
 x y z 
rv   , , 
 v v v 
an 
( a , ru  rv )
| ru  rv |
dS | ru  rv | dudv
S
a  {P ( x (u, v ), y (u, v ), z (u, v )),
Q ( x (u, v ), y (u, v ), z (u, v )),
R ( x (u, v ), y (u, v ), z (u, v ))}
 adS   a dS   (a , r  r )dudv
n
S
S
u

v
(ориентация S
согласована с
положительной
ориентацией
плоскости (u,v))
Поверхностный интеграл 2 рода
Случай поверхности, заданной как график явной функции z=φ(x,y),
и векторного поля параллельного оси Oz
a  {0,0, R} 
S

S
ru  1,0,  / x,
z   ( x, y )
S
 adS   Rdxdy
x  u
y  v


 z   ( u, v )

 ( u, v )  
rv  0,1,  / y,
ru  rv  { / x,  / y,1}
rv  ru  { / x,  / y, 1}
Для согласованных ориентаций:
(a , ru  rv )  R 
 adS   (a , r  r )dudv   R( x, y, ( x, y ))dxdy
u
S

v

Поверхностный интеграл 2 рода
z   ( x, y )
S

 R( x, y, z )dxdy    R( x, y, ( x, y ))dxdy
S

Знак плюс берется для согласованных ориентаций (проекция
нормали на ось Oz положительна) и минус иначе (проекция
нормали на ось Oz отрицательна).
Поверхностный интеграл 2 рода
x   ( y, z )
S
M ( y, z )

 P( x, y, z )dydz    P( ( y, z ), y, z )dydz
S

Знак плюс берется для согласованных ориентаций (проекция
нормали на ось Ox положительна) и минус иначе (проекция
нормали на ось Ox отрицательна).
Поверхностный интеграл 2 рода
y   ( z, x )
S
M ( z, x )

 Q( x, y, z )dzdx    P( x, ( z, x), z )dzdx
S

Знак плюс берется для согласованных ориентаций (проекция
нормали на ось Oy положительна) и минус иначе (проекция
нормали на ось Oy отрицательна).
Поверхностный интеграл 2 рода
Пример. Вычислить
 xdydz  ydzdx  zdxdy,
S
где S – внешняя сторона сферы x2+y2+z2=a2 (a>0).
Рассматриваемый интеграл представляет собой интеграл
второго рода от векторного поля
a  {x, y , z}.
Внешняя нормаль к сфере направлена по ее радиусу
n  {x, y , z}, (| n | a ),
Поэтому нормальная компонента векторного поля
(a , n ) x 2  y 2  z 2 a 2
an 


a
|n |
a
a
2
3
xdydz

ydzdx

zdxdy

a
dS

a
dS

a
|
S
|

a

4

a

4

a

 n

S
S
S
Поверхностный интеграл 2 рода
Пример. Вычислить
dydz dzdx dxdy
S x  y  z ,
где S – внешняя сторона эллипсоида
x2 y2 z2
 2  2  1.
2
a
b
c
z
c
y
a
x
b
 x  a cos  cos 

 y  b cos  sin 
 z  c sin 

0    2 , 

2
 

2
Поверхностный интеграл 2 рода
z'
a

a

y'
a
z
c
y
x
b
0    2 ,


2
 

2

x  x '

b

y

y'

a

c

z

z'

a
x'
a
 x '  a cos  cos 

 y '  a cos  sin 
 z '  a sin 

 x  a cos  cos 

 y  b cos  sin 
 z  c sin 

0    2 ,


2
 

2
Поверхностный интеграл 2 рода
dydz dzdx dxdy
I  


  adS ,
x
y
z
S
S
 x  a cos  cos 

 y  b cos  sin 
 z  c sin 

0    2 , 

2
1 1 1
a , , 
x y z
 

2
r  {a cos  sin  , b cos  cos  ,0}
r  {a sin  cos  , b sin  sin  , c cos  }
n  r  r  {bc cos2  cos  , ac cos2  sin  , ab sin  cos  } ( внешняя)

1
1
1 
a
,
,

 a cos  cos  b cos  sin  c sin  
(a , r  r ) 
bc cos  ac cos  ab cos   bc ac ab 


 
  cos 
a
b
c
b
c 
 a
Поверхностный интеграл 2 рода
I

 
0  2


 
( a , r  r )d d 
0  2


  
2
2
( a , r  r )d d 

  
2
2
2

2
 bc ac ab 
 bc ac ab 
      cos  d d       d  cos  d 
b
c  0 2
b
c 0
 a
 a




  
2
2
 bc ac ab 
 bc ac ab 
     (2 )  2  4    
b
c 
b
c 
 a
 a
Ответ:
 bc ac ab 
I  4    
b
c 
 a
2
Поверхностный интеграл 2 рода
Пример. Вычислить
 ( y  z )dydz  ( z  x )dzdx  ( x  y )dxdy,
S
где S – сторона конической поверхности x2+y2=z2 (0 ≤ z ≤ h) с
нормалью, имеющей отрицательную проекция на ось Oz.
z
a  { y  z, z  x, x  y}
y
x
Разобьем интеграл на три:
I   ( y  z )dydz   ( z  x )dzdx   ( x  y )dxdy
S
S
S
Поверхностный интеграл 2 рода
x
I1   ( y  z )dydz
S
S1
z
S2
y
zh
z  y
z

zy
y
Конус x2+y2=z2 пересекает плоскость
x=0 по прямым z=y, z=-y. Поверхность S
проектируется в треугольник Ω и
распадается на две поверхности S1 и S2.
S1 - это часть поверхности S, лежащая
над плоскостью yOz, а S2 - является
частью поверхности S, лежащей под этой
плоскостью.
Заданная нормаль к поверхности S1
имеет положительную проекцию на ось
Ox, а к S2 отрицательную.
I1   ( y  z )dydz   ( y  z )dydz   ( y  z )dydz   ( y  z)dydz  0
S1
S2


Поверхностный интеграл 2 рода
y
I 2   ( z  x )dzdx
S
S1
z
S2
x
zh
z  x
z

zx
x
Конус x2+y2=z2 пересекает плоскость
y=0 по прямым z=x, z=-x. Поверхность S
проектируется в треугольник Ω и
распадается на две поверхности S1 и S2.
S1 - это часть поверхности S, лежащая
над плоскостью xOz, а S2 - является
частью поверхности S, лежащей под этой
плоскостью.
Заданная нормаль к поверхности S1
имеет положительную проекцию на ось
Oy, а к S2 отрицательную.
I 2   ( z  x)dzdx   ( z  x)dzdx   ( z  x)dzdx   ( z  x)dzdx  0
S1
S2


Поверхностный интеграл 2 рода
z
I 3   ( x  y )dxdy
zh
y
x
y

S
Пересечение конуса x2+y2=z2 и плоскости
z=h проектируется в окружность x2+y2=h2.
Заданная нормаль к поверхности имеет
отрицательную проекцию на ось Oz, поэтому
I 3    ( x  y )dxdy   ( y  x )dxdy.

x

В полярных координатах
2
h
0
0
 ( y  x )dxdy   d  (r sin   r cos  )rdr 

2
Ответ:
I 0
h
h3
  (sin   cos  )d  r dr  0   0
3
0
0
2
Поверхностный интеграл 2 рода
Пример. Вычислить
I   x dydz  y dzdx  z dxdy ,
2
2
2
S
где S – внешняя сторона сферы
( x  a )2  ( y  b)2  ( z  c)2  R 2 .
z
c
I1   z 2dxdy
R
x yzx
S
y
x
a
b
I 2   x 2dydz
S
I 3   y dzdx
2
S
a b c a
I1  I 2  I 3
Поверхностный интеграл 2 рода
S1 : z1  c  R 2  ( x  a ) 2  ( y  b) 2
z
c S1
S 2 : z2  c  R 2  ( x  a ) 2  ( y  b ) 2
R
b
a
x
 : ( x  a )2  ( y  b)2  R 2
S2
y

I1   z 2dxdy   z 2dxdy   z 2dxdy   z12dxdy   z22dxdy    z12  z22  dxdy
S
S1


S2
z  z  c  R  ( x  a )  ( y  b)
2
1
2
2
2
2
2
  c 
2


R  ( x  a )  ( y  b)
2
 4c R 2  ( x  a ) 2  ( y  b) 2
2
2

2

Поверхностный интеграл 2 рода

y
I1    z12  z22  dxdy 
R

b
 4c  R 2  ( x  a )2  ( y  b)2 dxdy
x

a
 x  a  r cos 

 y  b  r sin 
2
R
0
0
I1  4c  d 

D ( x, y )
r
D( r,  )

0    2 , 0  r  R
 1 2 3 3/2  R
2
2
R  r rdr  4c  (2 )    R  r   0
 3

R3 8 3
 8 c  cR
3
3
Поверхностный интеграл 2 рода
a  b  c  a  I1  I 2  I 3
8 3
8
8 3
3
I1 
cR  I 2 
aR , I 3 
bR
3
3
3
8 3 8
8 3 8
3
I  I1  I 2  I 3 
cR 
aR 
bR 
(a  b  c ) R 3
3
3
3
3
Ответ:
8
I
(a  b  c) R 3
3
Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ.
Поверхностные интегралы.
Лекция 5
завершена.
Спасибо за внимание!
Тема следующей лекции:
Основные формулы векторного анализа.
Формула Грина.
Лекция состоится в четверг 16 октября
в 14:30 по Московскому времени.