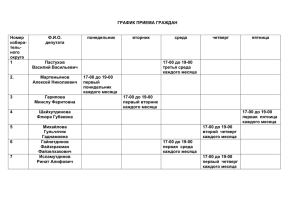
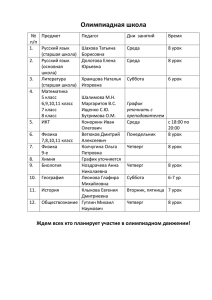
Решение задач части В. 11 класс
реклама

Решение текстовых задач части В. Прежде чем решать задачу- прочитай условие. Ж. Адамар Задача 1. В нашей школе обучаются 118 детей. В столовой на каждого школьника полагается 250 мл сока в день. Какое наименьшее количество литровых пакетов сока необходимо приобрести школе на 5 дней? Решение. 1) 0,25 · 118=29,5(л.) 2) 29,5 · 5=147,5(л.) Ответ: 148 литровых пакетов. Задача 2. По статистике, в Республике Мордовия из 100 семейных пар в возрасте от 25 до 40 лет в среднем 66 пар, в которых работают оба супруга, и 34 пары, в которых работает только один супруг. Сколько в среднем человек работает в 350 семейных парах? Решение. (66·2+34·1 )·3,5= (132+34)·3,5= =166·3,5=581(ч.) Ответ: 581 человек. Задача 3. Стоимость одной из моделей сотовых телефонов понизилась на 12% и составила 7150 руб. Сколько рублей стоила эта модель телефона до понижения цены? Решение. 100%-12%=88% 88%=0,88 7150 :0,88=8125 (руб.) Ответ: 8125 рублей. Задача 4. Пчеловод с 20 ульев в среднем получает 500 кг мёда. Из-за болезни несколько ульев с пчёлами перестали давать мёд, а выход мёда с каждого оставшегося улья уменьшился на 20%. Сколько ульев осталось у пчеловода, если он собрал 360 кг мёда? Решение. 500:20=25(кг) мёда получает с одного улья, 20%=0,2 25·0,2=5(кг) мёда составили потери с одного улья, 25-5=20(кг) мёда стал получать с одного улья из-за болезни пчёл. 360:20=18(ульев) Ответ: 18 ульев осталось у пчеловода. Иногда приходится говорить о трудных вещах, но следует делать это как можно проще. Г. Харди. Задача 5. Краснослободский маслозавод выпускает продукцию разных видов, среди них: сыр, творог, сметана. Массы производимым заводом сыра, творога и сметаны относятся как 3:5:8 соответственно. Завод планирует удвоить массу производимой продукции, при этом сыра должно производится на 80% больше, а творога на-60% больше, чем прежде. На сколько процентов нужно увеличить массу сметаны, чтобы реализовать этот план? Решение. Пусть х кг- приходится на 1 часть, у- доли процентов сметаны, 3х кг-масса сыра, 5х кг- масса творога, 8х кг- масса сметаны, всего: 3х+5х+8х=16х. (3х+3х · 0 ,8)=5,4х кг- масса сыра по плану, (5х+5х ·0,6)=8х кг- масса творога по плану , По условию задачи имеем: 5,4х+8х+(8х+8х · у)=32х, 8ху=10,6х, у=1,325. 1,325 · 100%=132,5% Ответ: на 132,5% увеличить массу производимой сметаны. Задача 6. Жарким летом 2010 года в пойменных лугах СХАП им. Калинина влажность свежескошенной травы составила 70%. Сколько тонн сена, влажность которого 20%, получилось из 6 тонн этой травы? Решение. 100%-70%=30%-приходится на сухую часть травы. Эта величина равна 6000·0,3=1800 (кг) После сушки 100%-20%=80%приходится на сухую часть сена от всей массы сена. Тем самым масса сена равна: 1800 : 0,8= 2250 (кг) Ответ: 2250 кг сена. Задача 7. Два ретрансляционных спутника за один час могут обработать 50 млрд. сигналов. Известно, что первый спутник может обработать 90 млрд. сигналов на 2 часа быстрее, чем второй-100 млрд. За сколько часов первый спутник может обработать 600 млрд. сигналов? Решение. Пусть Х ч.- время ΙΙ спут. на 100 млрд. сигн. (Х-2) ч.- время Ι спутника на 90 млрд. сигн. По условию задачи имеем: 90:(Х-2) +100:Х=50, 5Х²-29Х+20=0, Х1 =0,8- посторонний корень, Х2 =5 ч.- время ΙΙ спутника на 100 млрд. сигн. 5-2=3 (ч.)- время Ι спутника на 90 млрд. сигн. 90:3=30 (млрд.) сигн. в час обрабатывает Ι спутник 600:30=20 (ч.) Ответ: за 20 часов Ι спутник может обработать 600 млрд. сигналов. «Саранскстройинвест»: лидер в области строительства и продажи жилья в Республике Мордовия Задача 8. В четверг акции компании подорожали на некоторое количество процентов, а в пятницу подешевели на то же самое количество процентов. В результате они стали стоить на 9% дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг? Решение. Пусть х руб.- стоимость акций до торгов, у- доли процентов ( например, не 50% а, 0,5). Тогда (х+ху)руб. - стоимость акций в четверг, ((х+ху) - (х+ху)у)руб. - стоимость акций в пятницу. В результате они стали стоить на 9% дешевле т.е. (х- 0,09х)руб. По условию задачи имеем: ((х+ху) - (х+ху)у) = (х- 0,09х) 1-у² = 0,91 у² = 0,09 у1;2 = ±0,3 у = 0,3; 0,3·100%=30% Ответ: на 30% подорожали акции в четверг. Задача 9. Квартал леса заповедника им. П.Г. Смидовича содержал 96% сосен. Пожар уничтожил на этом участке 150 сосен, в результате чего их содержание понизилось до 95%. Сколько сосен осталось на этом участке? Решение. Пусть х- деревьев было на участке, 0,96х- было сосен до пожара, (0,96х-150)- осталось сосен после пожара, (х-150)- деревьев осталось после пожара, 0,95(х-150) -сосен осталось после пожара, По условию задачи имеем: (0,96х-150)= 0,95(х-150), х=750. 0,96 · 750-150=570 Ответ: 570 сосен осталось в данном квартале заповедника. Задача 10. На предприятии выработка продукции возросла за год на 4%, а на следующий год повысилась ещё на 8%. Найти средний годовой прирост за эти два года. Решение. Пусть х- средний, одинаковый для каждого года, процент прироста продукции; А1- количество продукции до повышения; А2- количество продукции после двух повышений; А2= А1(1+0,04)(1+0,08)-с одной стороны; А2= А1(1+0,01х)² - с другой стороны. По условию имеем: А1(1+0,04)(1+0,08) = А1(1+0,01х)² Ответ:? Если вы хотите научится плавать, то смело входите в воду, а если хотите научиться решать задачи- решайте их. Д.Пойа. Математическое открытие