отношением сигнал/шум
реклама

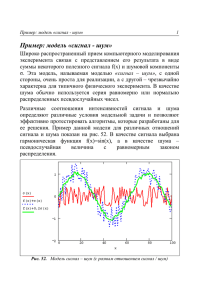
Лекция № 11 Линейная фильтрация. Линейная оптимальная фильтрация по критерию максимума отношения сигнал/шум Линейная фильтрация Для устранения вредного влияния шума на полезный сигнал можно применить частотноизбирательный линейный стационарный фильтр. Действительно, пусть сигнал обладает узкополосным энергетическим спектром, сосредоточенным в районе центральной 0плотность мощности частоты , а спектральная шума занимает более широкую полосу частот. Тогда фильтр, модуль частотного K jбольшой и коэффициента передачи которого равномерный в области сосредоточения энергетического спектра сигнала и мал на остальных частотах, будет заметно увеличивать относительную долю сигнала в результирующем колебании на выходе такого фильтра. Положим, что на входе фильтра действует аддитивная смесь u âő t полезного сигнала sâő t и шума nâő t : uâő t sâő t nâő t Кроме того, пусть сигнал sâő t и nâő t шум представляют собой некоррелированные и стационарные в широком смысле процессы, у которых средние значения равны нулю. В таком случае интенсивность колебаний на входе фильтра будем характеризовать значением среднего квадрата (средней мощности): u 2 âõ t s 2 âõ t n 2 âõ t 2 sâõt nâõt Однако ввиду некоррелированности сигналов sâő t и nâő t третье слагаемое sâő t nâő t 0 поэтому средний квадрат входного сигнала равен сумме средних квадратов полезного сигнала и шума: u âő t sâő t nâő t sâő t 2 2 где фильтра. 2 ďâő 2 2 2 ďâő - дисперсия шума на входе Следовательно, относительный уровень полезного сигнала sâő t по сравнению с шумом nâő t на входе фильтра можно охарактеризовать так называемым отношением сигнал/шум s âő t 2 Qâő 2ďâő Поскольку процессы и стационарные, то их средние квадраты не зависят от времени и отношение сигнал/шум представляет собой безразмерное число. Отношение сигнал/шум можно выразить и в логарифмических единицах (децибелах): qâő 10 lg Qâő Поскольку линейный фильтр удовлетворяет принципу суперпозиции, то на выходе получим колебание , uтакже âűő t представляющее собой аддитивную смесь преобразованных фильтром независимо полезного сигнала sâűő t и шума nâűő t : uâűő t sâűő t nâűő t Как следует из теории вероятностей, в этом случае и также будут некоррелированы и поэтому средний квадрат выходного колебания u âűő 2 t sâűő 2 t nâűő 2 t sâűő 2 t 2 ďâűő Далее так же, как и на входе фильтра, можно определить отношение сигнал/шум на выходе фильтра: 2 Qâûõ sâûõ t 2 ïâûõ или в логарифмических единицах qâűő 10 lg Qâűő Введем в рассмотрение величин Qâűő M Qâő которая носит название выигрыша фильтра по отношению сигнал/шум. Выигрыш фильтра также можно выразить в децибелах: m qâűő qâő Ясно, что положительный результат от воздействия фильтра на входное колебание будет лишь в том случае, если M 1 или m 0 Рассмотрим широко используемую в радиотехнике математическую модель узкополосного сигнала: S âő t Ak cos k t k k 0 Ak k k где амплитуда; - частота и - начальная k фаза -й гармонической компоненты сигнала. Найдем среднюю мощность этого сигнала, проведя усреднение по времени: T T 2 A 2 2 sâõ t lim sâõ t dt Ak2 lim cos 2 k t k dt k T T k 0 k 0 2 0 0 Если такой сигнал проходит через линейный фильтр с частотным коэффициентом передачи K j , то средняя мощность сигнала на выходе sâûõ 2 1 2 2 t Ak K j 2 k 0 Используя понятие одностороннего спектра мощности S стационарного случайного процесса, для дисперсии шума nâő t можем записать: 2 ďâő S n d 0 Тогда дисперсия фильтра 2 ïâûõ шума на выходе S n K j d 2 0 Выражение для отношения сигнал/шум на выходе фильтра: A 2 k Qâûõ K j 2 1 k 0 2 2 S K j d n 0 Зная спектры сигнала и шума с помощью этой формулы можно подобрать АЧХ K j линейного стационарного фильтра таким образом, чтобы получить требуемый выигрыш M фильтра по отношению сигнал/шум. При этом следует иметь в виду, что и сам полезный сигнал sâő t при прохождении через фильтр претерпевает определенные изменения. Поэтому фильтр необходимо подбирать таким образом, чтобы достичь требуемого значения M и не допустить существенных искажений сигнала. Конкретные требования как к значению выигрыша M , так и к допустимому уровню искажений полезного сигнала фильтром зависят от назначения конкретной радиосистемы. Линейная оптимальная фильтрация по критерию максимума отношения сигнал/шум Если линейный фильтр в соответствии с заданным критерием обрабатывает аддитивную смесь сигнала и шума наилучшим образом, то такой линейный фильтр называется оптимальным. Далее рассмотрим оптимальную линейную фильтрацию сигналов известной формы. Такая ситуация характерна для радиолокации, где принятый сигнал является точной масштабной копией переданного сигнала. Пусть на вход линейного стационарного ht фильтра с импульсной характеристикой воздействует сумма полезного сигнала sâő t и шума. На выходе линейного фильтра полезный сигнал создает отклик s âűő t s ht - d âő Попытаемся отыскать такую импульсную характеристику , ht чтобы величина sâűő t определяемая значением отклика фильтра в точке t0, достигала максимально возможного значения. Фильтр с такой импульсной характеристикой называется согласованным с заданным входным сигналом или кратко согласованным фильтром. Таким образом, необходимо отыскать такую импульсную характеристику ht , чтобы отклик на выходе в момент времени t0 достигал максимально возможного значения по модулю. (1) s âűő t 0 s h t d âő 0 Применим к правой части выражения известное неравенство ШварцаБуняковского в интегральной форме: 2 f x x dx f 2 x dx 2 x dx a a a b b b Получим: 2 b b sâő ht 0 - d sâő2 d h 2 t 0 - d a a Знак равенства в выражении достигается в том случае, когда подынтегральные функции пропорциональны друг другу, т.е. (2) h t - k s 0 âő Тогда, используя в выражении (2) замену переменной , получаем, что модуль правой части выражения (1) достигнет максимума при hńîăë t k sâő t0 - Следовательно, импульсная характеристика согласованного фильтра представляет собой масштабную копию входного сигнала, расположенную в зеркальном порядке на оси времени sвх t sвх t hсогл t 2 1 t0 0 1 2 t Как видно из рис., чтобы импульсная характеристика hńîăë t удовлетворяла условию физической реализуемости, т.е. hńîăë t 0 при t 0 ,необходимо, чтобы выполнялось неравенство t 0 2 . Применяя преобразование Фурье к обеим частям соотношения (2), находим частотный коэффициент передачи согласованного фильтра K ńîăë j h t e ńîăë ke jt 0 s z e âő jt jt dt k s âő t 0 - t 0 e dz ke jt dt j t 0 S * (3) Таким образом, частотный коэффициент передачи согласованного фильтра выражается через спектральную плотность полезного сигнала sâő t , для выделения которого из шума и предназначен фильтр. В формуле (3) коэффициент k определяет уровень усиления фильтра, а jt0 множитель определяет смещение e отклика фильтра по оси времени на время t0 . Особенностью согласованного фильтра является то, что при формировании отклика на своем выходе им используется как информация об амплитудно-частотном спектре входного сигнала, так и его фазово-частотный спектр. Фильтр с малым ослаблением должен пропускать лишь гармонические компоненты, частоты которых расположены в области, где спектральная плотность полезного сигнала отличается от нуля. Кроме того, фильтр выполняет коррекцию фазовых сдвигов гармонических составляющих входного сигнала таким образом, что в момент все эти гармонические составляющие складываются на выходе когерентно, имея одни и те же фазовые сдвиги. Тем самым отклик на выходе фильтра в момент достигает максимально возможного уровня (4) sâűő max kEs где . энергия полезного выделяемого сигнала Es s âő Из выражения (4) следует, что максимальное значение отклика согласованного фильтра не зависит от формы сигнала, а определяется его энергией. Найдем отношение сигнал/шум фильтра, определяемое как пикового значения мощности сигнала в момент к средней выходного шума: s âűő t 0 2 ďâűő 2 Qâűő на выходе отношение выходного мощности Для определенности положим, что шум nâő t представляет собой стационарный белый гауссов шум с равномерным спектром мощности уровня N 0 на всей числовой оси. В этом случае дисперсия шума на выходе 2 ïâûõ 1 2 2 k N0 N 0 K ñîãë j d 2 2 2 k N0 2 * d S S S d k 2 N 0 Es 2 Тогда, учитывая полученный результат и формулу (4), находим: 2 2 s s âűő 2 0 0 s Q k E E N k N E Таким образом, согласованный фильтр обеспечивает на выходе максимально достижимое отношение сигнал/шум и в этом смысле он является оптимальным. Перейдем теперь к вопросам синтеза согласованных фильтров. Для этого рассмотрим конкретный пример построения согласованного фильтра для прямоугольного видеоимпульса. s t 1 s t 2 A s t s t вых 0 u 2 t u s t 3 Положим, что импульс возникает в момент времени t 0 , имеет длительность u и амплитуду A . Найдем спектральную плотность такого сигнала: u A jt jt S sâő t e dt A e dt 1 e jt (5) j 0 Найдем частотный коэффициент передачи фильтра K ńîăë j в предположении, что на его выходе максимум отклика достигает в момент u , т.е. t 0 u. В соответствии с формулой (3) и с учетом (5), находим: kA kA j u j u j u K ñîãë j 1 e e e 1 j j (6) kA j u 1 e j Выражение (6) позволяет синтезировать искомый согласованный фильтр. Он состоит из идеального видео усилителя с коэффициентом усиления , интегратора, которому в частной kA области соответствует умножение на , линии задержки1 /на jвремя u и вычитающего устройства. На вычитающее устройство в соответствии с формулой (6) подается напряжение по двум каналам: непосредственно с интегратора и через линию задержки. На выходе согласованного фильтра получаем сигнал треугольной формы высотой kEs и длительностью 2 u : t u s âűő t kEs 1 0 t 2 u u где энергия прямоугольного видеоимпульса E s A 2 u . Согласованный фильтр s t s t s t s t вх kA 1 + 2 вых s t 3 u Для некоторых простых по форме сигналов с небольшой базой удается добиться приемлемых результатов при их линейной фильтрации более простыми в конструктивном исполнении фильтрами по сравнению с оптимальными. Такие фильтры называют квазноптимальными, т.е. фильтрами, близкими по характеристикам к оптимальным. Рассмотрим простую интегрирующую RCцепочку с импульсной характеристикой 1 t ht exp где RC постоянная времени цепи. Пусть на вход такой цепи воздействует сумма полезного сигнала в виде прямоугольного видеоимпульса и гауссов белый шум со спектральной плотностью мощности N 0 . В этом случае отклик на воздействие полезного сигнала достигает максимума при t 0 u . Таким образом, находим: s âűő max t s âűő u s z h âő u - z dz u 0 A e u z u dz A1 e Частотный коэффициент интегрирующей RC-цепи 1 K j 1 j Дисперсия шума на выходе будет: 2 ďâűő N0 0 2 передачи N0 N0 d K j d 2 2 0 1 2 Отсюда максимальное значение отношения сигнал/шум на выходе RC-цепи A 1 e N0 2 2 Qâűő max u 2 1 e E s N 0 u 2 u 2 (7) Как следует из предыдущих результатов, первый сомножитель правой части соотношения (7) равен максимальному отношению сигнал/шум на выходе согласованного фильтра, а второй сомножитель 2 u 1 e u 2 характеризует проигрыш в отношении сигнал/шум интегрирующей RC-цепи по сравнению с согласованным фильтром. Второй сомножитель достигает максимума при / 1,25 , равного 0,814. u Таким образом, при соответствующем выборе постоянной времени RC-цепи получим, что интегрирующая RC-цепь при фильтрации прямоугольного видеоимпульса на фоне шума проигрывает в эффективности (в смысле отношения сигнал/шум на выходе) всего лишь на 18,6 %. Именно RC-цепь с такими характеристиками и будет квазиоптимальным согласованным фильтром для прямоугольного видеоимпульса.