Задача № 1.36
Условие:
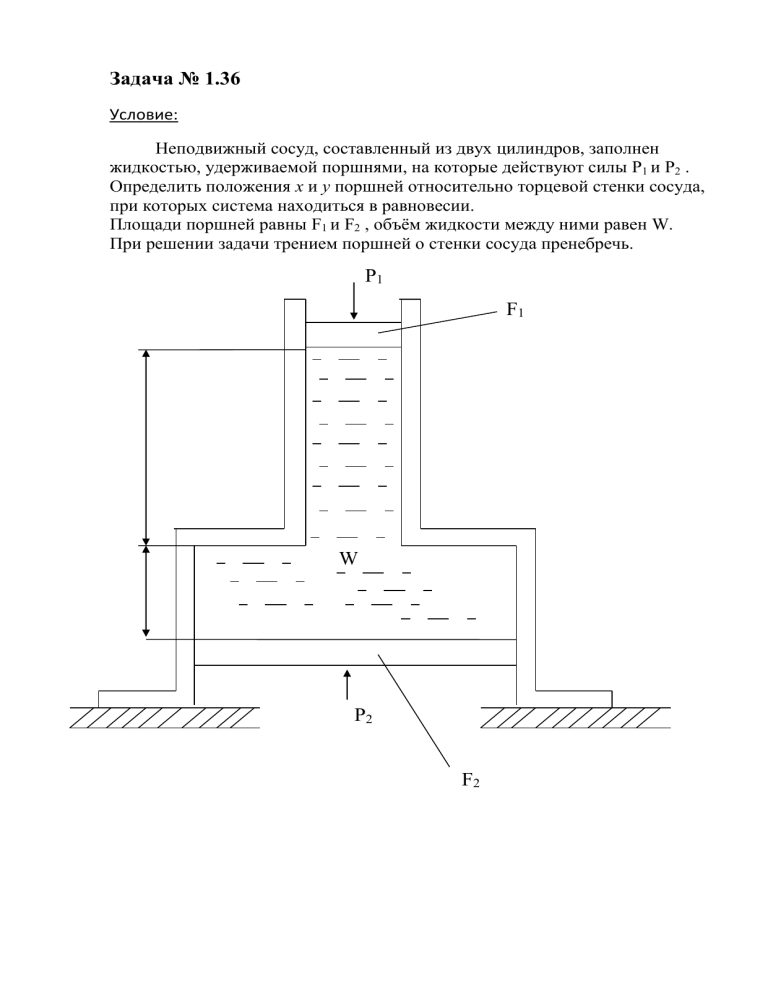
Неподвижный сосуд, составленный из двух цилиндров, заполнен
жидкостью, удерживаемой поршнями, на которые действуют силы P1 и P2 .
Определить положения x и y поршней относительно торцевой стенки сосуда,
при которых система находиться в равновесии.
Площади поршней равны F1 и F2 , объём жидкости между ними равен W.
При решении задачи трением поршней о стенки сосуда пренебречь.
P1
F1
W
P2
F2
Решение:
В состоянии равновесия сила, действующая на нижний поршень,
уравновешивается силой, действующей на верхний поршень и силой
давления жидкости объемом W.
P2 = P1 F2 /F1 +(W+ (F2- F1)x)pg;
P2 - P1 F2 /F1 =(W+ (F2- F1)x)pg;
P2 - P1 F2 /F1 =(F2- F1)x;
pg
P2 – P1F2 /F1 –Wpg =x;
Pg(F2 – F1)
Положение нижнего поршня найдем из уравнения объема:
xF1 + yF2 = W;
(P2 – P1F2 /F1 –Wpg )F1 – W = - yF2;
Pg(F2 – F1)
W/F2 - P2F1 – P1F2 –WpgF1/F2 = y;
Pg(F2 – F1)
Ответ: P2 – P1F2 /F1 –Wpg ; W/F2 - P2F1 – P1F2 –WpgF1/F2 ;
Pg(F2 – F1)
Pg(F2 – F1)
Задача 2.1
Условие:
В плотине сделан прямоугольный проем размером H x C, через который вода
поступает к турбине. При ремонте турбины этот проем закладывается семью
специальными балками – шандорами. Размер каждой шандоры h x B = 1,2 x
3,4 м. Все шандоры имеют по две пары катков.
1. Определить силы давления воды P1 и P7 на первую и седьмую шандоры
и максимальные изгибающие моменты M1 и M7 для этих шандор, а
шандоры – свободно опертыми.
2. Найти расстояния ∆h1 и ∆h7 между центром давления и центром
тяжести смоченной поверхности для первой и седьмой шандор.
1
2
3
4
5
6
7
B
Решение:
1. Определим силы давления на первую и седьмую шандору:
P1 =pghc1S;
Так как каждая шандора представляет собой параллелепипед, то центр
тяжести у неё будет находиться на пересечении диагоналей.
hc1 = 0,6;
P1 = 1000 ∙ 9,8 ∙ 0,6 ∙ 1,2 ∙ 3,4 = 23990,4 Н = 24 кН;
P7 = pghc7S = pgS(H-hc1) = 1000 ∙ 9,8 ∙ 1,2 ∙ 3,4 ∙ (8,4 − 0,6) =
311875,2 Н = 312 кН;
2. ∆ℎ1 = hD1 – hC1 , где hD1 - центр давления
∆ℎ1= Jc /Shc1;
Для данной шандоры Jc =hb3/12;
∆ℎ1 =
3,4∙1,23
12∙0,6∙1,2∙3,4
∆ℎ7 = Jc /Shc7 =
= 0,2 м = 20см ;
3,4∙1,23
12∙7,8∙1,2∙3,4
= 1,5 см;
3. Момент инерции симметричной стенки равен Jc=1/12bhc3;
Изгибающий момент М=pJcg;
M1 = pgJc1 = pg 1/12 bhc13= 1000 ∙ 9,8 ∙
3,4∙0,63
M7 = pgJc7 = pg 1/12 bhc73 = 1000 ∙ 9,8 ∙
12
= 10,2 кН ∙ м;
3,4∙7,83
12
= 133 кН ∙ м;
Ответ: P1 = 24кН; P2 = 312кН; ∆ℎ1 = 20см; ∆ℎ7 = 1,5см; М1 = 10,2 кН ∙
м; М7 = 133 кН ∙ м;
Задача № 3.1
Условие:
Определить величины и направления сил давления воды на плоское и
полусферическое днища цилиндрического сосуда диаметром D=1м в трех
случаях:
Y=+D/5; y= -D/5; y=0;
Показать в виде векторов горизонтальные и вертикальные составляющие сил
давления воды на днища.
Решение:
1. Определим величины сил давления воды на плоское и полусферическое
днища для первого случая y=D/5;
1 2∙3,14∙0,52
Для полусферического: Pг=рgShc1 = 1000 ∙ 9,8 ∙ ∙
5
1
1
6
6
2
= 1,54 кН;
Pв = 𝑝 ∙ 𝑔 ∙ 𝑉1 =𝑝 ∙ 𝑔 ∙ ∙ 𝜋 ∙ 𝑅3 = 1000 ∙ 9,8 ∙ ∙ 3,14 = 2,57кН;
Для плоского днища: 𝑃г = 𝑝 ∙ 𝑔 ∙ ℎ𝑐 ∙ 𝑆 = 𝑝 ∙ 𝑔 ∙ ℎ𝑐 ∙
𝜋𝐷2
4
1 3,14
= 1000 ∙ 9,8 ∙ ∙
5
4
=
1,54 кН;
2. При y=-D/5;
1
2∙3,14∙0,52
5
2
Для полусферического: Pг=рgShc1 = 1000 ∙ 9,8 ∙ (− ) ∙
1
1
6
3
= −1,54 кН;
Pв = 𝑝 ∙ 𝑔 ∙ 𝑉1 =𝑝 ∙ 𝑔 ∙ ∙ 𝜋 ∙ 𝑅3 = 1000 ∙ 9,8 ∙ ∙ 3,14 = 2,57кН;
Для плоского днища: 𝑃г = 𝑝 ∙ 𝑔 ∙ ℎ𝑐 ∙ 𝑆 = 𝑝 ∙ 𝑔 ∙ ℎ𝑐 ∙
3,14
4
𝜋𝐷2
4
1
= 1000 ∙ 9,8 ∙ (− ) ∙
5
= −1,54 кН;
3. При y=0;
Для полусферического: Pг=рgShc1 = 1000 ∙ 9,8 ∙ (0) ∙
1
1
6
6
2∙3,14∙0,52
2
= 0;
Pв = 𝑝 ∙ 𝑔 ∙ 𝑉1 =𝑝 ∙ 𝑔 ∙ ∙ 𝜋 ∙= 1000 ∙ 9,8 ∙ ∙ 3,14 = 2,57кН;
Для плоского днища: 𝑃г = 𝑝 ∙ 𝑔 ∙ ℎ𝑐 ∙ 𝑆 = 𝑝 ∙ 𝑔 ∙ ℎ𝑐 ∙
3,14
4
𝜋𝐷2
4
= 1000 ∙ 9,8 ∙ (0) ∙
= 0;
Ответ: для полусферического днища во всех трех случаях горизонтальная
составляющая равна 1,54кН, -1,54кН, 0 соответственно, вертикальная во
всех трех случаях равна 2,57кН. Для плоского днища во всех случаях
горизонтальная составляющая равна 1,54кН, -1,54кН, 0.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
Высшего профессионального образования
«Уфимский государственный нефтяной технический университет»
Кафедра гидравлики и гидромашин
Дисциплина «Гидравлика»
РГР №1
Вариант №
Выполнил студент гр. МТ-10-01
___________________
Д. Д. Абдуллин
Принял доцент
___________________
Л. Р. Байкова
Уфа 2012
