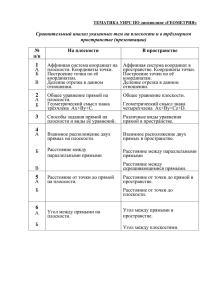
Расстояние от точки до плоскости

«Различные подходы
к решению задач С2 в рамках
Единого государственного экзамена»
Критерии оценивания
задания С2
Содержание критерия
Баллы
Обосновано получен верный ответ
2
Решение содержит обоснованный переход
к планиметрической задаче, но получен
неверный ответ или решение не закончено,
или при правильном ответе решение не
достаточно обосновано.
Решение не соответствует ни одному из
критериев, перечисленных выше.
1
0
Виды задач С 2:
• Расстояние от точки до прямой
• Расстояние от точки до плоскости
• Расстояние между скрещивающимися
прямыми
• Угол между двумя прямыми
• Угол между прямой и плоскостью
• Угол между плоскостями
Основные методы решения
задачи С 2
• поэтапно-вычислительный(метод опорных задач )
(традиционный метод опирается на определения расстояния или
угла, и требует от учащихся развитого пространственного
воображения, применение данного метода состоит в
применении известных опорных задач, которые в большинстве
случаев формулируются как теоремы)
• метод координат (универсальный метод, может быть
использован при решении задач любого вида)
• применение векторов
(также может быть использован при решении задач любого вида)
• применение формул (площади ортогональной проекции
многоугольника, объёма пирамиды, высоты треугольника,
параллелограмма или трапеции).
Расстояние от точки до прямой
• Расстояние от точки до прямой, не содержащей эту
точку, есть длина отрезка перпендикуляра ,
проведенного из этой точки на прямую.
• Расстояние между двумя параллельными прямыми
равно длине отрезка их общего перпендикуляра.
• Расстояние между двумя параллельными прямыми
равно расстоянию от любой точки одной из этих
прямых до другой прямой.
a
h
b
Расстояние от точки до прямой (поэтапновычислительный метод)
Задача (ЕГЭ-11г): В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1, стороны основания которой равны 4, а
боковые рёбра равны 1, найдите расстояние от точки В до прямой
F1E1.
Решение опирается на определение расстояния :
Т.к. A1B1C1D1E1F1 - правильный
шестиугольник, то прямые В1F1 и F1E1
перпендикулярны, следовательно, прямые
BF1 и F1E1 перпендикулярны( по ТТП).
Расстояние от точки В до прямой FE1
равно длине отрезка BF1.Из ∆
В1F1=4√3,тогда из ∆ ВF1B1 : BF1 = 7.
Ответ: 7.
Расстояние от точки до прямой можно
вычислить, как длину отрезка перпендикуляра, если удается
включить этот отрезок в некоторый треугольник в качестве
одной из высот (по формуле)
Задача: В правильной шестиугольной пирамиде
SABCDEF стороны основания которой равны 1, а
боковые рёбра равны 2 , найдите расстояние от точки
F до прямой BG, где G – середина ребра SC.
Решение: Искомое расстояние от
точки F до прямой BG равно
высоте FH треугольника FBG, в
котором FB = FG =√3 (FG – высота
равностороннего треугольника SFC).
Из ∆BSC
BG 
3
2
BG 
1
3
ВН 
BG 
2
2 2
По теореме Пифагора находим
6
.
2
42
FH 
.
4
Расстояние от точки до прямой (координатный метод)
Задача:
В правильной шестиугольной пирамиде SABCDEF стороны основания
равны 2, а боковые рёбра – 3. Найти расстояние от вершины S
пирамиды до прямой МК, где М – середина АВ, К – середина SE.
3

3
MS  ;
;2 3 
2 2

S
z
S
К
D
y
C
B
A
М
F
S (1; 3;2 3 )
1 3
M ( ;
;0)
2 2
E (3; 3;0)
K (2; 3; 3 )
К
E
O
М
h
5

3
MK  ;
; 3
2
2

 3 7 3
3
M S  M K  ;
;

2
2
2


x
 ( S ; MK )  h 

Sпар.
h
9 147 3


4
4
4 
25 3
 3
4
4

MS  MK
MK
159
.
40

Расстояние от точки до прямой (векторный метод)
Задача (Тр. 4, №8): В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найти
расстояние от точки В до прямой АD1.
Решение
Пусть Н – ортогональная проекция
точки В на прямую AD1.
H  AD1  А H  A D1.
Н
H  AD1  АН   AD1
BH  AD1  BH  AD1  0
B H  A H  A B  ( AH  AB)  AD1  0
2

A
D
 A B  A D1  0
(A D1  A B )  A D1  0;
1
AD  2; AD1  5 ; BD  3; BD1  2; cos BAD1 
.
5
1
1
1
  5  1 5 
 0  
5
5 B H  A D1  A B  5 A D1  A B .
BH
2
1
1
1
4
2 5

 5  1  2   5 1 
  BH 
.
25
5
5
5
5
•Расстояние от точки до плоскости, не содержащей эту точку,
есть длина отрезка перпендикуляра, опущенного из этой точки на
плоскость.
•Расстояние между прямой и параллельной ей плоскостью
равно длине их общего перпендикуляра.
•Расстояние между прямой и параллельной ей плоскостью
равно расстоянию от любой точки этой прямой до плоскости.
•Расстояние между двумя параллельными плоскостями равно
длине их общего перпендикуляра.
•Расстояние между двумя параллельными плоскостями равно
расстоянию между точкой одной из этих плоскостей и другой
плоскостью.
Расстояние от точки до плоскости
Расстояние от точки M до плоскости α :
1) равно расстоянию до плоскости αот произвольной точки P,
лежащей на прямой l , которая проходит через точку M и
параллельна плоскости α ;
2) равно расстоянию до плоскости α от произвольной точки P ,
лежащей на плоскости α, которая проходит через точку M и
параллельна плоскости α .
β
α
Р
М
l
Расстояние от точки до плоскости
(поэтапно-вычислительный метод)
В единичном кубе A…D1 найдите расстояние от
точки A до плоскости BDA1.
3
.
Ответ:
3
Решение: Диагональ AC1 куба
перпендикулярна плоскости BDA1.
Обозначим O - центр грани ABCD,
E - точка пересечения AC1 и
плоскости BDA1. Длина отрезка
AE будет искомым расстоянием. В
прямоугольном треугольнике
AOA1 имеем
2
6
AA1 = 1; AO =
; OA1 =
.
2
2
3
Следовательно, AE =
.
3
В единичном кубе A…D1 найдите расстояние от точки
A до плоскости CB1D1.
Решение: Плоскость CB1D1
О
параллельна плоскости BDA1, и
отстоит от вершины C1 на
расстояние 3 .
3
(см. предыдущую задачу).
Учитывая, что длина диагонали
куба равна 3 , получим, что
2 3
искомое расстояние AF равно
.
3
2
3
Ответ:
. Выводы: расстояние между параллельными
3
3
плоскостями A1DВ и СВ1D1 равно 3 .
Расстояние от точки С до плоскости А1BD равно расстоянию от точки О до
3
плоскости A1DB и равно
.
3
В кубе ABCDA1 B1 C1 D1 диагональ AC1 перпендикулярна плоскостям A1BD и
CB1D1и делится ими на три равные части.
Расстояние от точки до плоскости
(поэтапно-вычислительный метод)
Тр.р.№6. Задача№6.В правильной шестиугольной пирамиде SABCDEF,
стороны основания которой равны 1, а боковые рёбра равны 2, найдите
расстояние между прямыми SB и AF.
Решение. AF параллельна плоскости ESB,
SB лежит в плоскости ESB. Задача
сводится к нахождению расстояния от AF
до плоскости ESB. Это есть AH ┴BE.
В трапеции ВAFE BE=2. AF=1,BH=1/2. По
теореме Пифагора находим AH:
н
1
3
AH  1  
.
4
2
Ответ:
3
2
Расстояние от точки до плоскости
(метод объемов)
Если объем пирамиды АВСМ равен V ABCM , то
расстояние от точки M до плоскости α , содержащей
треугольник АВС, вычисляют по формуле
3VABC
 ( М ; )   ( М ; АВС ) 
S ABC
В общем случае рассматривают равенство
объемов одной фигуры, выраженные двумя
независимыми способами.
Расстояние от точки до плоскости (метод объемов)
Задача (Тр. 5, №1): В единичном кубе А…D1 найдите расстояние от
точки А до плоскости СB1D1.
Решение
Пусть АН – искомое расстояние –
высота пирамиды ACB1D1.
Н
Применим формулу
объёма пирамиды:
1
V  Sосн.  h
3
VAB1CD1  Vкуба  4VC1CB1D1 
1 1
 1 4  
6 3
3V
3 2 3
AH 
 1:

S
2
3
Расстояние от точки до плоскости (по формуле)
В правильной пирамиде SABCD, все ребра которой равны
1, найдите расстояние от точки A до плоскости SBC.
Решение. Обозначим E, F – середины ребер AD, BC. Искомое
расстояние равно высоте EH треугольника SEF, в котором
6
3
SE = SF =
, EF = 1. Откуда, EH =
.
3
2
6
Ответ:
.
3
Расстояние от точки до плоскости (координатно-векторный метод).
Задача (Тр. 5, №1): В единичном кубе А…D1 найдите
расстояние от точки А до плоскости СB1D1.
(0;0;1)
Решение.
z
Пусть АН – искомое расстояние
(1;1;1) АН ┴(CB D );Н(х;у;z); АН{x-1;y;z}
1 1
Н
АН ┴D1B1{1;1;0} АН ┴CB1{1;1;0}
(0;1;0) у
АН ┴CH {x;y-1;z}
AH  D1B1  0; AH  B1C  0; AH  СH  0
х (1;0;0)
( х  1) 1  у  0

( х  1)х (1)  0
( х  1)  х  у  ( у  1) 

1 

x



3


2 

y



3


2


2
z


z  0 
3


 2 2 2
AH  ; ;  
 3 3 3
2 3
AH 
.
3
Уравнение плоскости имеет вид
ax + by + cz + d = 0 ,где коэффициенты –
координаты вектора нормали к плоскости (вектора,
перпендикулярного плоскости).

B(x2,y2,z2)
M(x,y,z)
n ( a , b, c )
A(x1,y1,z1)
C(x3,y3,z3)
x  x1 y  y1 z  z1
x2  x1 y2  y1 z2  z1  0
x3  x1 y3  y1 z3  z1
Раскрыв определитель третьего порядка, получим
уравнение плоскости.
Расстояние от точки до плоскости (координатный метод)
Задача (Тр. 5, №1): В единичном кубе А…D1 найдите
расстояние от точки А до плоскости СB1D1.
(0;0;1)
Решение
z
(1;1;1)

Н
(0;1;0)
у
х (1;0;0)
ах0  ву0  cz0  d
a b c
где А( x0 , y0 , z0 ),
2
2
2
,
n a, b, c вектор нормали.
х у 1 z
0
1
1 1  0
0
0
 x  y 1 z  0
11  0  (1)  0  (1) 2 3
х

x  y  z 1  0  
111
3
Расстояние между скрещивающимися прямыми
Расстояние между двумя скрещивающимися
прямыми равно длине отрезка их общего перпендикуляра.
α
Расстояние между скрещивающимися
прямыми
1) равно расстоянию от любой точки одной из
этих прямых до плоскости, проходящей через
вторую прямую параллельно первой прямой;
2) равно расстоянию между двумя
параллельными плоскостями,
содержащими эти прямые;
a
α
β
в
a
3) равно ρ (a;b) = ρ (A;b) , где A = a α , b = b1 :
если ортогональная проекция на плоскость α
переводит прямую а в точку А, а прямую b в
прямую b1 , то расстояние между
α
скрещивающимися прямыми а и b равно
расстоянию от
точки А до прямой b1.
А
b1
Расстояние между скрещивающимися прямыми
h
Vпар.
Sосн.

(С1D1 , CB, CC1 )
CB  C1D1
Расстояние между скрещивающимися прямыми (координатный метод)
В прямоугольном параллелепипеде ABCDA1B1C1D1 стороны основания равны 3 и
2, а боковые рёбра равны 4. На ребре СС1 отмечена точка К так, что СК : КС1 =
1:3. Найти расстояние между прямыми ОК и МD,где М – середина В1С1,О –точка
пересечения диагоналей основания.
М
В1
С1
z 1
А1
1
D1
А
О (1,5;1;0)
МD (1,5;-2;-4)
К (3;2;1)
ОК (1,5;1;1)
4
К
М (0;0;2)
С
D (3;0;0)
у
В
Решение
О
2
3
D х
 15 9 
OK  MD   2; ; 
2 2


МO (0;-1;-4)

1,5 1 1
21
OK , MD, MO  1,5  2  4 
2
0

1

4
21
h
2

225
81
4

4
4
21
322
Расстояние между скрещивающимися прямым
(поэтапно-вычислительный метод)
Тр.р.№6.Задача №6. В правильной шестиугольной пирамиде SABCDEF,
стороны основания которой равны 1, а боковые рёбра равны 2, найдите
расстояние между прямыми SB и AF.
Решение.
Н
AF ║BE
AF ║( BSE)
Задача сводится к
нахождению расстояния от AF
до плоскости BSE. Проведём
AH ┴BE.
В трапеции BAFE BE = 2, AF =
1,
BH = ½, AB= 1.
1
3
AH  1  
4
2
Ответ:
3
2
Расстояние между скрещивающимися прямыми (векторный метод)
Тр.р.№6. Задача №3. В правильной треугольной призме АВСА1В1С1,
все стороны которой равны 1, найдите расстояние между прямыми АВ
и СВ1.
Решение.
Пусть FN –общий перпендикуляр прямых АВ и СВ1
Введём базисные векторы:



АА1  a, ВВ1  в , СС1  с.

a
N

в

с
F
  
В1С  В1В  В1С1  в  с  а.
  
 
FN  FB  BB1  B1N  xc  a  y(b  c  a)
FN  AB  FN  AB  0
FN  B1C  FN  B1C  0

 

 
( xc  a  yb  yc  ya )  c  0
 


 
( xc  a  yb  yc  ya )  (b  c  a )  0
1
x y 0
1 2
 x  2y 1
2
2
21



3 4 2
FN  a  b  c FN  49  FN 
7 7 7
21
7
2
x 
7
4
y 
7
Ответ:
21
7
Угол между прямыми
b
- пересекающимися

a
b


a
b1
- скрещивающимися
26
Угол между прямыми
• Углом между двумя пересекающимися прямыми
называется наименьший из углов, образованных при
пересечении прямых.
•Углом между скрещивающимися прямыми
называется угол между пересекающимися прямыми,
соответственно параллельными данным
скрещивающимся.
• Две прямые называются перпендикулярными,
если угол между ними равен 900 .
• Угол между параллельными прямыми считается равным
нулю.
Задача
Трапеция АВСD (AD и ВС – основания) и треугольник АЕD
лежат в разных плоскостях. МР – средняя линия ∆АЕD.
Чему равен угол между прямыми МР и АВ, если АВС = 110°.
В
С
Ответ: 70°
D
А
P
M
E
Если прямая лежит в одной из двух перпендикулярных плоскостей, то
угол между прямой и плоскостью равен углу между этой прямой и
линией пересечения плоскостей.
Угол между прямыми (координатный метод)
b
В
А
Алгоритм решения:
1. A(x1;y1;z1); B (x2;y2;z2);
С
C(x3;y3;z3); D(x4;y4;z4).
D
a
2. AB и CD
3. AB и CD
4. cos  
AB  CD
AB  CD
.
29
Угол между прямыми (координатный метод)
Задача. В правильной четырехугольной пирамиде SABCD, все ребра
которой равны 1, отмечены точки E и F — середины сторон SB и SC
соответственно. Найдите угол между прямыми AE и BF.
Решение.
z
у
x
Введем прямоугольную систему координат:
начало в точке A, оси x и y направим
вдоль AB и AD соответственно, а ось z
направим вертикально вверх. Единичный
отрезок равен AB = 1. Точки E и F —
середины отрезков SB и SC
соответственно, поэтому их координаты
находятся как среднее арифметическое
концов. Выпишем координаты
интересующих нас точек:
Угол между прямыми (координатный метод)
A = (0; 0; 0); B = (1; 0; 0)
z
Зная точки, найдем координаты
направляющих векторов AE и BF:
у
Координаты вектора AE совпадают
с координатами точки E, т.к.точка A —
начало координат. Найдём косинус угла:
x
3 1 2 
AE  ; ;

4 4 4 
 1 3 2
BF  ; ;

 4 4 4 
Ответ: arccos (1/6)
Угол между прямыми (векторный метод)

а
l1
l2

в
a b
cos(l1 , l2 )    ,
a b
   
 
где a  b  a  b cos( a , b ).
Угол между прямыми считается не превосходящим
900, а косинус такого угла положительным.
32
Угол между прямыми (векторный метод)
Задача №3диагн. р.2, В правильной шестиугольной призме
A…F1, все рёбра которой равны 1, найдите косинус угла
между прямыми AB1 и BD1.
Решение. Введём базисные векторы:



АА1  a, AB  в , AF  с.

a
 
AB1  a  b , BC  BA  AF  FC 
 
  
 b  c  2b  b  c
BD1  BC  CC1  C1D1 


      
в
с

b

c

a

c

a

b

2
c
    
AB1  BD1  (a  b )  (a  b  2c )  1
1
2
BD  3 , BD1  2, AB1  2 сos( AB1; BD1 ) 

4
2 2
Теорема о трех перпендикулярах:
Если прямая, проведенная на
плоскости через основание
наклонной, перпендикулярна ее
проекции, то она перпендикулярна
наклонной.
И обратно: Если прямая на
плоскости перпендикулярна
наклонной, то она перпендикулярна
и проекции наклонной.
34
Угол между прямыми (поэтапно-вычислительный метод)
Задача №1диагн. р.2, В кубе A… D1 найдите угол между прямыми
AB 1 и BD1.
Решение.
А1В – ортогональная
проекция BD1 на
плоскость ВАА1.
( АВ1; A1B)  90.
По теореме о трёх
перпендикулярах:
( BD1; AB1 )  90.
Ответ: 90°
Угол между прямыми (поэтапно-вычислительный метод)
В1
Е
K
5
4
С1
2
2
2
А1
D1
1
5
4
А
F
В
С
М
1
2
Р
D
Ответ: cosα = 0,8
Угол между прямой и плоскостью
Углом между наклонной и плоскостью называется
угол между этой наклонной и ее ортогональной
проекцией на данную плоскость.
Считают также, что прямая, перпендикулярная
плоскости, образует с этой плоскостью прямой угол.
Угол между прямой и плоскостью
B

n


C
D
A
E


AB  n
sin   cos( n; AB) 
AB  n
Угол между прямой и плоскостью
(поэтапно-вычислительный метод)
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол
между прямой AB1 и плоскостью ADE1.
Решение: Плоскость BB1F1
перпендикулярна плоскости ADE1 и
пересекает ее по прямой QF1. В
прямоугольном треугольнике QB1F1
имеем: QB1 = 2, B1F1 = 3 . Высота
B1H этого треугольника равна 2 21.
7
В прямоугольном треугольнике AB1H
имеем: AB1 = 2 , B1H = 2 21 ,
7
Следовательно, sin  
Ответ: sin  
42
.
7
42
.
7
Угол между прямой и плоскостью (координатно-векторный метод)
Задача. В правильной треугольной пирамиде ABC боковое ребро равно √3, а
сторона основания равна 2√2. Найти угол между боковым ребром SA и
плоскостью боковой грани SBC.
Решение. Поместим пирамиду в прямоугольную систему координат так, что точка
О – центр треугольника, лежащего в основании( точка пересечения медиан).
z
1
2 2
D(0;0; ), B(
;0;0),
3
3
2
2
C (
; 2; 0), A(
; 2 ;0)
3
3
у
х
Уравнение плоскости SBС
задаётся в виде:
аx  by  cz  d  0,
где (a, b, c)  координатынормали.
1
с  d  0,
3
2 2
a  d  0,
3

2
a
3
2b  d  0;
Угол между прямой и плоскостью (координатно-векторный метод)
Задача. В правильной треугольной пирамиде DABC боковое ребро равно √3, а
сторона основания равна 2√2. Найти угол между боковым ребром DA и
плоскостью боковой грани DBC.
Решение. Поместим пирамиду в прямоугольную систему координат так, что точка
О – центр треугольника, лежащего в основании( точка пересечения медиан).
z
1
2 2
D(0;0; ), B(
;0;0),
3
3
2
2
C (
; 2; 0), A(
; 2 ;0)
3
3
у
х
Уравнение плоскости SBС
задаётся в виде:
аx  by  cz  d  0,
где (a, b, c)  координатынормали.
1
с  d  0,
3
2 2
a  d  0,
3

2
a
3
2b  d  0;
Угол между прямой и плоскостью (координатно-векторный метод)
c   3d ,
с   3d ,
3
a
d,
2 2
3
a
d,
2 2
3
b
d.
2 2
2b  d 
2
3
3
(
)d   d ;
2
3 2 2
Уравнение плоскости принимает вид:
3x  3 y  2 6 z  2 2  0

Вектор нормали:
n 3;3;2 6
3
3

x
y  3z  1  0;
2 2
2 2
 2
; 2;
Вектор AD 
 3
2 3 2 2
Находим угол между данными векторами: cos  
3  9  24 


он равен синусу угла наклона бокового ребра SA к
плоскости грани SBC:
1 
.
3
2 6 2
2


,
3
3 6 3
  arcsin
2
.
3
Угол между прямой и плоскостью (координатно-векторный метод)
c   3d ,
с   3d ,
3
a
d,
2 2
3
a
d,
2 2
3
b
d.
2 2
2b  d 
2
3
3
(
)d   d ;
2
3 2 2
Уравнение плоскости принимает вид:
3x  3 y  2 6 z  2 2  0

Вектор нормали:
n 3;3;2 6
3
3

x
y  3z  1  0;
2 2
2 2
 2
; 2;
Вектор AD 
 3
2 3 2 2
Находим угол между данными векторами: cos  
3  9  24 


он равен синусу угла наклона бокового ребра DA к
плоскости грани DBC:
1 
.
3
2 6 2
2


,
3
3 6 3
  arcsin
2
.
3
Угол между прямой и плоскостью
(традиционный метод с применением формул)
M
Задача. В правильной треугольной
пирамиде DABC боковое ребро равно √3, а
сторона основания равна 2√2. Найти угол
между боковым ребром DA и плоскостью
боковой грани DBC.
O
T
Решение. Сделаем некоторые
дополнительные построения:
BC  AT , BC  DT  BC  ( ADT ) 
 ( ADT )  ( DBC ). ( ADT )  ( DBC )  DT
Проведём АМ ┴ DT, получим, что отрезок АМ ┴ (DBC), и проекцией
отрезка AD на плоскость (DBC) является отрезок DM.
Для нахождения угла ADM дважды запишем выражения для площади
1
треугольника ADT:
6
DO  AT
3
1
1
AM


 2
S ADT  DO  AT  AM  DT ;
DT
1
2
2
AM
sin ADM 

AD
2
.
3
Ответ :arcsin
2
.
3
Угол между прямой и плоскостью
(традиционный метод с применением формул)
M
Задача. В правильной треугольной
пирамиде DABC боковое ребро равно √3, а
сторона основания равна 2√2. Найти угол
между боковым ребром DA и плоскостью
боковой грани DBC.
O
VDATC
T
Задачу можно решить по – другому, если
заметить, что
1
1
 AM  SDTC  VDABC.
3
2
Угол между двумя плоскостями (двугранный угол)
равен углу между перпендикулярными к этим плоскостям прямыми.
Будем считать угол между плоскостями острым (или прямым).
Величина двугранного угла измеряется величиной
соответствующего линейного угла.
Чтобы построить линейный угол двугранного угла,
нужно взять на линии пересечения плоскостей
произвольную точку, и в каждой плоскости провести
из этой точки луч перпендикулярно линии
пересечения плоскостей. Угол, образованный этими

лучами и есть линейный угол двугранного
угла:
Угол между двумя плоскостями
Угол между плоскостями измеряется углом между
нормалями ( n и m ) к этим плоскостям.
 
nm
cos     ,
nm


где na1 , b1 , c1, ma2 , b2 , c2 
Величиной угла между плоскостями называется величина
меньшего двугранного угла.
Пусть плоскости 1 и  2 заданы уравнениями:
1 : a1x  b1 y  c1z  d  0
2 : a2 x  b2 y  c2 z  d  0
Косинус угла между плоскостями находится по такой
формуле:
cos  
a1a2  b1b2  c1c2
a b c  a b c
2
1
2
1
2
1
2
2
2
2
2
2
cos , так как величиной
В ответе мы записываем
угла между плоскостями называется величина меньшего
двугранного угла.
Угол между плоскостями (поэтапно-вычислительный метод)
Задача (СтатГрад-12г). В правильной четырёхугольной призме
ABCDA1B1C1D1 стороны основания равны единице, а боковые рёбра
равны 5.На ребре АА1 отмечена точка Е так, что АЕ : ЕА1 = 2:3. Найти
угол между плоскостями АВС и ВЕD1.
Решение.
Прямая D1Е пересекает прямую АD в точке
К. Плоскости ABC и BED1 пересекаются по
EA1 = AA1 – AE =3.
прямой КВ.
ЕН ┴ КВ, АН ┴КВ.
Угол АНЕ – линейный угол двугранного угла
между плоскостями ABC и BED1 .
∆AКЕ~ ∆A1D1E
AK 
AE
2
 A1D1 
EA1
3
AE 
2 AA1
2
5
13
В ∆АКВ <А=90° BK  AB  AK  3
AK  AB 2 13
Высота AH 

.
BK
13
AE

Из АНЕ (А  90 ) tgAHE 
 13.
Ответ :arctg 13.
AH
2
2
Угол между плоскостями ( по формуле)
Задача (СтатГрад-12г). В правильной четырёхугольной призме
ABCDA1B1C1D1 стороны основания равны единице, а боковые рёбра
равны 5. На ребре АА1 отмечена точка Е так, что АЕ : ЕА1 = 2:3. Найти
угол между плоскостями АВС и ВЕD1.
Решение.
D1
1
∆ ABD – ортогональная проекция ∆ BED1.
С1
Поэтому для нахождения искомого угла
1
можно использовать формулу площади
А1
ортогональной проекции:
В1
5
Sпр.
S пр.  S м н.  cos 
cos  
3
S м н.
D1B  12  12  52  27  3 3
Е D
С
BE  22  12  5
D1E  32  12  10
2
14
А
В
S

BE  BD  D1E
cos B 
2  BE  BD1
2
2
1
2
11
14
cos B 
 sin B 
3 15
3 15
BED1
2
SABD 1 14
1
cos  
 :

SBD1E 2 2
14
  arccos
1
.
14
Угол между плоскостями (координатный метод)
Задача (СтатГрад-12г). В правильной четырёхугольной призме ABCDA1B1C1D1
стороны основания равны единице, а боковые рёбра равны 5. На ребре АА1
отмечена точка Е так, что АЕ : ЕА1 = 2:3. Найти угол между плоскостями АВС
и ВЕD1.
Решение.
D1
(0;1;5)
С1
Составим уравнение каждой плоскости:
5
x y z
x 1 y z
( АВС ) : 1 0 0  0 ( BED ) :  1 0 2  0
1
1 1 0
1 1 5
z 1
А1
1
3
(0;0;2)
Е
у
D
2
А
В1
С (1;1;0)
х
(0;0;0)
В (1;0;0)
0  x  0  y  1 z  0
 2  x  3 y  z  2  0
n10;0;1 n2  2;3;1
 
n1  n2
 
1
14
cos   cos( n1; n2 )    

n1  n2
14 14
14
  arccos
.
14
Угол между плоскостями (векторный метод)
Задача (СтатГрад-12г). В правильной четырёхугольной призме
ABCDA1B1C1D1 стороны основания равны единице, а боковые рёбра
равны 5. На ребре АА1 отмечена точка Е так, что АЕ : ЕА1 = 2:3.
Найти угол между плоскостями АВС и ВЕD1.
Решение.
D1
1
С1
Выберем базисные векторы:
1
А1
В1
1

5


3

с



BA  a; BC  b ; BB  c
a  b  1; c  5
 
cos(( BED1 ); ( ABC ))  cos( p; с )
Е D
С


2
b
где с   ABC ; p  BED1  
А
В



a

p

BE
и
p

BD
1






p  xa  yb  zc
p  BE  0 и p  BD1  0
Угол между плоскостями (векторный метод)
D1
1
С1
1
А1
В1

с
3
Е
2
А
D

a
В
5


 2
( xa  yb  zc )  (a  c )  0
   5 

( xa  yb  zc )  (a  b  c )  0
2 2
xa  zc  0
52
2
xa  yb  zc 2  0
2
С
b
x 10z  0
x  y  25 z  0
Пусть z  1  x  10; y  15
 



2 
p  p ;c 5
p  10a  15b  c
  (10a  15b  c )  с
pс
 
1
cos( p  с )    

.
pс
100  225  25  5
14
Ответ :
14
arccos
.
14
Информационные ресурсы
• Павлов А.Н. Лекции курса « Особенности методики обучения
математике в условиях новой формы итоговой аттестации за курс
средней школы».
• Смирнов В. А.. «ЕГЭ 2013. Задача С2.Геометрия. Стереометрия.»
• Севрюков П.Ф., Смоляков А.Н. «Векторы и координаты в решении задач
школьного курса стереометрии».
• Корянов А.Г., Прокофьев А.А. « Типовые задания С2. Виды задач и
методы их решения.»
• Геометрия. 10–11 классы: учеб. для общеобразоват. учреждений:
базовый
• и профил. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.].–
М.: Просвещение, 2011.
• 2. Единый государственный экзамен 2012. Математика. Универсальные
материалы для подготовки учащихся / ФИПИ– М.: Интеллект-Центр,
2012.