Глинщикова Татьяна Геннадьевна учитель математики МОУ «Красноярская СОШ»

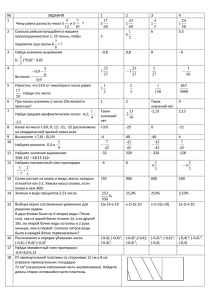
Глинщикова Татьяна
Геннадьевна
учитель математики МОУ
«Красноярская СОШ»
Любинского района
Стержень учебновоспитательного процесса
– личность учителя
Основная идея – быть
интересным людям,
дарить радость
Важно
Найти свой ключ
– ключ к самому себе,
уроку, сердцу ребёнка
Направления работы
Из копилки опыта:
• Создание опорных схем и ведение
тетради опорных конспектов
• Моделирование
• Проект урока по ТПДО
• Модель тьюторского сопровождения в
школе
• Работа с классом с использованием ИКТ
МОДЕЛИРОВАНИЕ
Модель – условный образ
сложного объекта.
Виды моделей:
• План
• Уравнение
• Описание
• Изображение
• Схема
• Чертёж
• Граф
• График
• Живые модели
Примеры решения задач
с помощью моделей
Задача 1.
Автомобиль проехал
расстояние от A до B за 14
минут, а мотоциклист ехал ему
навстречу и проехал это
расстояние за 35 минут.
Определите время встречи?
Модель - график
S
14
35
0
10
35
t
Задача 2.
Магазин наценил на 25% закупочную
цену товара. После продажи 0,8 всего
товара назначенная цена была снижена
на 40%, и оставшийся товар распродан.
Сколько процентов от закупочной цены
составила прибыль?
Модель – самостоятельное
введение данного
Пусть начальная цена равна 100 руб.
100
75
15
125*0,8+(125*0,6)*0,2=115 руб.
15 руб =15% - прибыль
Задача 3.
Два насоса выкачивают воду из
котлована
за
12
часов.
Производительность одного насоса в 1,5
раза меньше другого. За сколько часов
можно будет выкачать воду из котлована,
если сначала половину выкачает первый,
а остальное – второй насос?
Модель – двумерная диаграмма
t
25
Ответ: 25 часов
II
M
12
6
I
N
6
+9
15
производительность
Почему?
Если через произвольную точку Е диагонали АС
прямоугольника АВСD проведены прямые FG||AB и
HJ||AD, то
1) Образовавшиеся при этом прямоугольники HBGE и
FEJD равновелики;
2) Прямоугольники ABGF и AHJD также равновелики;
3) Отрезки FH, DB, JG параллельны.
B
G
C
E
H
A
J
F
D
Задача 4
Из двух сплавов с 60% и 80%
содержанием меди требуется получить
сплав в 40 кг. с 75% содержанием меди.
Сколько кг. каждого сплава следует взять
для этого?
4
часть
0, 8
3
L
2
0, 7
0, 6
1
10
40
m
Построение:
1. строим прямоугольник со
сторонами 40 x 0,75
2. проводим через отметку
0,6 отрезок, параллельный
горизонтальной оси
3. соединим отметку 0,8 и
точку, полученную при
пересечении отрезка,
проведённого в п.2 и
отрезка, проходящего
через отметку 40 кг
4. через точку L проводим
отрезок до пересечения с
горизонтальной осью. Он
и укажет на отметку 10.
Задача 5
Из двух городов, находящихся на
расстоянии 700 км, отправились
одновременно навстречу друг другу два
поезда; скорость одного из них на 20 км/ч
больше скорости другого. Найти скорости
движения каждого поезда, если известно,
что они встретились через 5 часов после
начала движения.
S I  S II  700
S заштрих  20  5  100 
прям оуг
t
B
5
C
S ABCD  700  100  600
  x  60 (км / ч)
S ABCD  AB  BC  10  x 
x  20  80 (км / ч)
20
x
x+20
Ответ: 80 км/ч и
5
A
D
60 км/ч
Задача 6
Слиток сплава серебра с цинком весом
в 3,5 кг содержал 76% серебра. Его
сплавили с другим слитком и получили
новый весом в 10,5 кг, серебра в
котором было 84% .Сколько процентов
серебра содержалось во втором
слитке?
часть серебра
7
x
x
0, 84
7  x  3,5  0,84  0,76
7  x  3,5  0,08 | : 7
x  0,5  0,08
0, 76
x  0,04
0,84  0,04  0,88  часть серебра во II слит
3, 5
10, 5
m, кг
Задача 7
Поезд проходит расстояние от города A
до города B за 10 час. 40 мин. Если бы
скорость поезда была на 10 км/час
меньше, то он пришел бы в B на 2 часа 8
мин. позже. Определить расстояние
между городами и скорость поезда.
Модель – двумерная диаграмма
(с использованием подобия
треугольников)
∆QRM ~ ∆LON
P
Q
ОК=х, ON=x-10
32/15 час
L
R
M
32/15 : 32/3 = 10 : (х-10)
1/5 = 10 : (x-10)
X-10=50
32/3 час
X=60км/ч – V1
N
O
Скорость
K
60*32/3=640 км – S
10 км/час
Задача 8
В равнобедренную трапецию с боковой
стороной 13 см вписана окружность
радиуса 2,5 см. Найти площадь трапеции.
B
S -?
Модель – граф
C
13
2,5
S-?
D
A
S=0.5*(BC+AD)*h
h=2*r
BC - ?
h=2*2.5=5
…
AD - ?
Длинный
путь
S=0.5*AC*BD*sin a
sin a -?
BC+AD=2*CD
(свойство описанного
4-угольника)
…
S=CD*h
S = 13*5=65
AC=BD - ?
…
Задача 9
Коллекцию значков разложили в
несколько коробок по 10 отделений в
каждой. В отделении коробки может
находиться только 1 значок. Любые 2
коробки отличаются друг от друга
наличием или отсутствием значков хотя
бы в одном отделении. Сколько коробок?
Модель – переформулировка
задачи
Пусть есть таблица из 10 столбцов. В каждой
клетке стоит либо 1, либо 0. Любые 2 строки
отличаются числом в клетке хотя бы одного
столбика. Сколько строк?
Ещё одна переформулировка: Сколько
различных 10-значных чисел можно составить
из 0 и 1 ?
Ответ: 210 = 1024
Опорные схемы – модели текстовой
информации, закодированной
знаками, рисунками
Правило сложения
рациональных чисел:
При сложении чисел с одинаковыми
знаками в ответ знак ставится тот же, а
модули чисел складываются. При
сложении чисел с разными знаками в
ответ ставится знак числа с большим
модулем, а модули вычитаются
Примерная схема правила:
(+) + (+) = (+)
( - ) + ( -) = ( -)
(+) + (-) =
знак
большего
модуля
Модули
Модули
сложить
вычесть
Для чего нужны схемы?
1. Самостоятельный поиск кодировки заставляет осмыслить правило,
выбирать главное, учит творчеству, вызывает интерес.
2. Схемы удобны для запоминания.
3. Раскрашивание схем в зеленый (основное правило), красный
(особенности) и синий (примеры) цвет подключает мощный
механизм зрительной и моторной памяти.
4. Схемы удобны для работы.
5. Позволяют разнообразить работу: восстанавливать пропущенные
части схемы, всю схему, раскрашивать черно-белую схему,
составлять варианты текстовой формулировки, примеры, вопросы
товарищам.
6. Ведение тетради опорных конспектов позволяет иметь под рукой
компактный справочник и возможность быстрого повторения.
1,2
,дес
цел.
3,02
,сот
5,003
,тыс
дроб.
1,2000 или 5=5,0
сравнение:
по целым
13,7812,95
по дробным
13,5113,48
13,1913,20
,
под
+5,0
7,2
,
1,2
0,6
0,72
Сколько вместе
целое
под
целым
пустые
_6,00
3,17
0
0
0
Делитель - целый
0,4 2
0,2
Целую часть : обязательно
_3 2
2 1,5
_10
10
0
4 ,8 .
0,12
4 80
12
· и : на 10,100,…
·
,
1,2 · 100=120
,
:
12 : 10 = 1,2
Длина
10
10
10
1000
1мм  1см  1дм  1м  1км
1мм = 0,1см = 0,01дм = 0,001м = 0,000001км
Масса
1000
100
10
1г  1кг  1ц  1т
Площадь
100
100
100
100
100
100
1мм2  1см2  1дм2  1м2  1ар  1га  1км2
Объем
1000
1000
1000
1мм3  1см3  1дм3  1м3
1л
(с n
)
n
метод: ИЗБАВЛЕНИЕ ОТ
(СПОСОБЫ)
n
, n>3
Не имеющие
смысла
n
n
Взаимно
обратные
выражения
Похожие
выражения
Корни кратных
степеней
Замена
переменной
Уединение
Возведение в
n – степень.
При возведении в
четную степень
могут появиться
посторонние корни
проверка
С полным
квадратом
a a
2


Решений нет
проверка
чет
f  d  П .ч.
f 0
d 0
П .ч.  0
f  П .ч.
f   П .ч.
n
П .ч.  0
2  х2  х  0
2  х2  х
2  х2  х2; х  0
х2  1
х1  1(ист), х 2  1( пост.)
ответ : х  1
х 
х  12
4
х  t  0
4
x  (4 x ) 2  t 2
t 2  t  12  0
t1  3
t 2  4( неудовл. условиюt  0)
x  3
x  81(ист)
4
81 
4
81  12
9  3  12
2)
1)
х 1

х 1
2
1

х 1
х 1 2

х 1
х 1
х 1
х 1
t 0
х 1
х 1
1
 (t  0)
х 1
t
2
2
х 2  3х  5  х 2  3х  7
х 2  3 х  5  х 2  3 х  5  12
t 0
t2
3)
y2  4y  8 
y2  4y  4 
t0
t2
t2 
2t
4) х 2  5 х  4  5 х 2  5 х  28
t0
t  5 t  24
2( y 2  4 y  6)
x 2  2x  1  5
x 1  5
x 1  5
x1  6
x  1  5
x 2  4
x2  5 x  x6
x20
5 x  0
смысл
х60
х2
х5
х6
Если вас заинтересовала наша
работа, мы можем представить:
• Весь материал по моделированию,
опорные схемы.
• Проект урока по ТПДО.
• Презентацию классных часов с
использованием ИКТ.
• Практические занятия на базе вашей
школы .
Достижения и результаты
•
•
•
•
•
•
•
•
•
Самообразование – изучаемые темы: дифференцированный подход к обучению, сочетание
различных технологий, приемы подготовки к ЕГЭ, личностно-ориентированное обучение.
Способы повышения квалификации: при ОГПУ (тестовая методика-144 ч), при ИРООО
(современные технологии-102 ч +36 ч ИКТ).
Овладение современными технологиями: использование ТПДО в среднем звене, проблемномодульного обучения в старшем, проектного обучения на факультативах, НОУ, элективных курсах.
НОУ: дипломы лауреатов областной НПК по математике (2007), экономике (2008), дипломы
участников Всероссийского фестиваля научно-исследовательских работ «Портфолио»(2009).
Внеклассная работа: разработка элективного курса «Секреты моделирования», проведение
занятий тест-класса, факультатива «Подготовительный курс», проведение предметных декад,
интеллектуальных марафонов, подготовка к очным и заочным олимпиадам, конкурсам «Кенгуру»
(2 место во Всероссийской заочной олимпиаде- 2007, 2009; 2 место в региональном конкурсе
«Кенгуру»-2008, 2009; 1 место на зональной олимпиаде- 2006, 1 место в районной-2007, 2008).
Тьюторство: наставничество (Ионина Н.В. – начинала работу в паре, вышла на самостоятельный
уровень в НОУ, выступлениях на конференциях, Саранча Н.В. – успешно применяет схемные и
знаковые модели в сочетании с ТПДО, Иванова Л.Ю. – начала работу в НОУ); достижения
подопечных: дипломы 1 степени в «Мегапроекте», поступление в выбранные учебные заведения,
выступления в различных конкурсах («Социальная звезда», «Талантливая молодежь»).
Методическая работа: выпуск брошюры «Урок – в радость»; обобщение опыта на школьном МО2007, на заседании ассоциации «Импульс», выпуск брошюры «Моделирование»-2008, выступление
с опытом внеклассной работы на семинаре заместителей директоров по ВР-2007, распространение
опыта на региональном уровне (заочная конференция ПНПО, курсы – 2009, на Всероссийском
уровне (Фестиваль «Открытый урок», «Портфолио»)
Участие в конкурсах: лауреат областного этапа конкурса «Учитель года-2004», дипломант конкурса
«Социальная звезда»-2005, победитель конкурса в рамках ПНПО -2006, победитель конкурса песен
к юбилею Любинского района -2009.
Внеучебная работа: кружок литературного творчества (лауреат Всероссийского конкурса -2003,
участие в областной НПК по литературному и декоративно-прикладному творчеству),
руководство школьным Пресс-центром, участие в экологических районных акциях ( грамоты);
организация походов, поездок (ТЮЗ, 5 театр, г.Одесса, Золотое кольцо).
Спасибо за внимание!