Документ 4762131

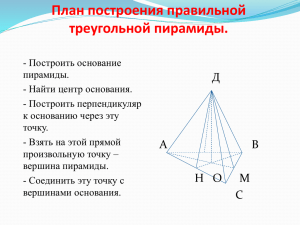
Математика в природе
млн
Совершенствовать навыки решения типовых
задач на нахождение объема пирамиды.
Сформировать навыки нахождения объема
пирамид, у которых вершина
проектируются в центр вписанной или
описанной окружности около основания.
Развивать наглядное образное мышление
учащихся.
Дано: FABCDEK – правильная
пирамида.
FO (АВС). FM AK, FO=4


FM =5. Найти V пирамиды.
Решение
1) V= 1 Sосн*Н
F
3
B
2) FOM – прямоугольный
OM = 52  42=3
3) Так как АВСDEK правильный
шестиугольник, то ОМ=r;
АК=2rtg300=2 3
C
A
M
O
D
K
4) Sосн=6*S
АОК=6*

E
5)V= 1 *18
3
1 *2 *3=18
3
3
2
3 *4=24 3
Если боковые ребра
пирамиды равны (или
составляют равные
углы с плоскостью
основания), то
вершина
проектируется в центр
окружности описанной
около основания.
S
В
С
O
А
Д
Если все двугранные
углы при основании
пирамиды равны (или
равны высоты боковых
граней, проведенные
из вершины
пирамиды), то
вершина пирамиды
проектируется в центр
С окружности, вписанной
в основание
пирамиды.
F
L
А
O
N
K
В
r=Rcos
a3=R 3
a3=r 3
r= 1 R
a4=R 2
a4=2r
r= 2R
a6=R
a6= 2
an=2Rsin
3
4
6
180
n
an=2rtg 180
n
n
2
3r
3
2
r= 3R
2
180
n
Дано: SАВС пирамида,
АВС прямоугольный
( В=900), АВ=6см,
ВС=8см. Каждое
боковое ребро
составляет с
плоскостью основания
угол 450.
Найти: Vпирамиды.
Дано: FABC пирамида,
 АВС равнобедренный,
АВ=АС=10см, ВС=12см,
FA=FC=FB=15см.
Найти: Vпирамиды.
B
S
А
O
С
S
В
А
O
M
C
Первый вариант.
1) Вершина проектируется в центр окружности, описанной около
основания. О - середина АС.
2) АС= 62  82 =10см. R=ОА=ОВ=ОС=5см
3)  SOB прямоугольный, Н=5см
1
4) Sосн= 2*6*8=24см2
5)V= 13 *24*5=40см3
Второй вариант.
1)Вершина проектируется в центр описанной окружности около
основания. R=ОА=ОВ=ОС
2) S = р( р  а)( р  b)( р  с) =48см2
25
авс
авс
3) S =
, R=
, R= 4
4R
4S
2
5
 25 
2
119
4) FO= 15    =
4
 4 
1
5
5) V= 3*48* 119=20 119
4
Первый вариант.
Второй вариант.
1)б
1)а
2)а
2)б
3)б
3)в
4)в
4)а
5)а
5)б