Метод итераций

Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ
1 семестр
Лекция 13
Длина кривой.
Касательная и кривизна.
Приближенные методы
решения уравнений.
11 декабря 2014 года
Лектор: Профессор НИЯУ МИФИ, д.ф.-м.н.
Орловский Дмитрий Германович
Длина кривой
 x  f1 (t ),

 y  f 2 (t ),
 z  f (t )
3

 t
Если функции f1(t), f2(t), f3(t)
непрерывно дифференцируемы,
то кривая L называется гладкой
кривой (кривая класса С1).
Условие регулярности
[ f1 '(t )]2  [ f 2 '(t )]2  [ f 3 '(t )]2  0
для спрямляемости кривой не обязательно.
Длина кривой
Теорема. Гладкая кривая спрямляема и ее длина удовлетворяет
неравенствам
m12  m22  m32 (   )  | L |  M12  M 22  M 32 (   ),
где
m j  Inf | f j ' (t ) |, (1  j  3),
[ ;  ]
M j  Sup | f j ' (t ) |, (1  j  3).
[ ;  ]
Длина кривой
Рассмотрим гладкую кривую
L  {( x; y; z ) : x  f1 (t ), y  f 2 (t ), z  f 3 (t ),   t   }
( f1 (t ), f 2 (t ), f 3 (t )  C 1[ ;  ]).
Пусть
M (t )  ( f1 (t ); f 2 (t ); f 3 (t ))
( A  M ( ), B  M (  )).
l (t ) |  AM (t ) |
Теорема. Для любой гладкой кривой
l ' (t )  [ f1 ' (t )]2  [ f 2 ' (t )]2  [ f 3 ' (t )]2 .
M (t )
Длина кривой
Доказательство. Пусть t>t0, тогда по теореме об аддитивности длины
l (t )  l (t0 ) | M (t0 )M (t ) |
Согласно предыдущей теореме для отрезка [t0;t]
m12  m22  m32 (t  t0 )  l (t )  l (t0 )  M12  M 22  M 32 (t  t0 )
l (t )  l (t0 )
 M 12  M 22  M 32
t  t0
mi | f i ' (ξ i ) |, t 0  ξ i  t , 1  i  3,
m12  m22  m32 
M i | f i ' (ηi ) |, t 0  ηi  t , 1  i  3.
lim ξ i  lim ηi  t0  lim | fi ' (ξ i ) | lim | fi ' (ηi ) || f i ' (t0 ) | .
t t0
t t0
t t0
t t0
l (t )  l (t0 )
lim
 [ f1 ' (t0 )]2  [ f 2 ' (t0 )]2  [ f 3 ' (t0 )]2
t t 0 0
t  t0
Длина кривой
Если t<t0, тогда
l (t0 )  l (t ) | M (t )M (t0 ) |
Согласно предыдущей теореме для отрезка [t; t0]
m12  m22  m32 (t0  t )  l (t0 )  l (t )  M12  M 22  M 32 (t0  t )
l (t0 )  l (t )
 M 12  M 22  M 32
t0  t
mi | f i ' (ξ i ) |, t  ξ i  t 0 , 1  i  3,
m12  m22  m32 
M i | f i ' (ηi ) |, t  ηi  t 0 , 1  i  3.
lim ξ i  lim ηi  t0  lim | fi ' (ξ i ) | lim | fi ' (ηi ) || f i ' (t0 ) | .
t t0
t t0
t t0
t t0
l (t )  l (t0 )
l (t0 )  l (t )
lim
 lim
 [ f1 ' (t0 )]2  [ f 2 ' (t0 )]2  [ f 3 ' (t0 )]2
t  t 0 0
t  t 0 0
t  t0
t0  t
Длина кривой
l (t )  l (t0 )
 [ f1 ' (t0 )]2  [ f 2 ' (t0 )]2  [ f 3 ' (t0 )]2
t t 0 0
t  t0
lim
l (t )  l (t0 )
lim
 [ f1 ' (t0 )]2  [ f 2 ' (t0 )]2  [ f 3 ' (t0 )]2
t  t 0 0
t  t0
Отсюда следует, что
l ' (t )  lim
t t 0
l (t )  l (t0 )
 [ f1 ' (t0 )]2  [ f 2 ' (t0 )]2  [ f 3 ' (t0 )]2
t  t0
Длина кривой
Элемент длины дуги
Определение. Модуль дифференциала длины дуги называется
элементом длины дуги.
ds | l ' (t )dt | [ f1 ' (t )]2  [ f 2 ' (t )]2  [ f 3 ' (t )]2 | dt | (dx) 2  (dy) 2  (dz) 2
(теорема Пифагора в дифференциалах).
Особенно наглядное значение эта формула имеет для плоской
кривой, являющейся графиком явно заданной функции y=f(x).
График явно заданной функции всегда можно представить в
параметрической форме. Для этого достаточно взять в качестве
параметра независимую переменную.
Длина кривой
x  t,

 y  f (t ),
 z  0.

ds  [ x' (t )]2  [ y ' (t )]2  [ z ' (t )]2 | dt |
 1  [ f ' (t )]2  0 | dt | 1  [ f ' ( x)]2 | dx |
 (dx) 2  (dy ) 2
ds  (dx) 2  (dy ) 2
Касательная к кривой
 x  f1 (t ),

 y  f 2 (t ),
 z  f (t ).
3

Касательная к кривой
Предельное значение этого вектора при t→t0
a  { f1 ' (t0 ); f 2 ' (t0 ); f 3 ' (t0 )}
(в том случае, когда оно отлично от нулевого вектора) называется
касательным вектором к кривой в точке t0.
Прямая, проходящая через точку M(t0) с этим направляющим
вектором, называется касательной к кривой в точке t0.
Касательная к кривой
Особые и регулярные точки кривой
 x  f1 (t ),

 y  f 2 (t ),
 z  f (t ).
3

[ f1 ' (t )]  [ f 2 ' (t )]  [ f 3 ' (t )]  0  регулярная точка
2
2
2
[ f1 ' (t )]2  [ f 2 ' (t )]2  [ f 3 ' (t )]2  0  особая точка
В регулярной точке кривая всегда имеет касательную.
Касательная к кривой
Пример 1.
x  t 3 ,

3
y  t ,
 z  0.

Пример 2.
 x  t | t |,

2
y

t
,

 z  0.

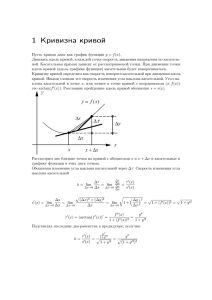
Кривизна плоской кривой
Средняя кривизна на участке:
k ср |

s
|
Кривизна в точке M(t0):
k  lim kср  lim
t t 0
t t 0
|  |
s
Кривизна плоской кривой
Теорема. Пусть на плоскости задана гладкая регулярная кривая
 x   (t ),

 y   (t ).
Тогда ее кривизна в каждой точке t0 определяется формулой
k
|  ' (t0 ) ' ' (t0 )   ' ' (t0 ) ' (t0 ) |
(|  ' (t0 ) |2  |  ' (t0 ) |2 )3 / 2
Замечание.
Гладкая:
 ,  C 1
Регулярная:
|  ' (t ) |2  | ' (t ) |2  0
Кривизна плоской кривой
Доказательство. Так как кривая регулярна, то величина
|  ' (t ) |2  | ' (t ) |2  0
Пусть для определенности
 ' (t )  0
Касательный вектор к кривой
a  { ' (t ); ' (t )}
образует с осью абсцисс угол
  arctg
 ' (t )
 ' (t )
Кривизна плоской кривой
По определению кривизны

 (t )   (t0 )
k  lim
 lim

t t0 s
t t0 s ( t )  s ( t )
0
( (t )   (t0 )) / (t  t0 )
 lim

t t0 ( s ( t )  s ( t )) / ( t  t )
0
0

lim( (t )   (t0 )) / ( t  t0 )
t t0
lim( s(t )  s(t0 )) / ( t  t0 )
t t0

 '(t0 )
s '( t0 )
Кривизна плоской кривой
Так как
 ' (t )  (arctg
 ' (t )
1
 ' (t )
)' 
(
)' 
2
 ' (t )
1  ( ' (t ) /  ' (t ))  ' (t )
[ ' (t )]2
 ' ' (t ) ' (t )  ' (t ) ' ' (t )  ' (t ) ' ' (t )   ' ' (t ) ' (t )



2
2
2
[ ' (t )]  [ ' (t )]
[ ' (t )]
[ ' (t )]2  [ ' (t )]2
s ' (t )  [ ' (t )]2  [ ' (t )]2  ([ ' (t )]2  [ ' (t )]2 )1/ 2
то
k
 '(t ) ''(t )   ''(t ) '(t )
2
2 1/2
/
([

'(
t
)]

[

'(
t
)]
) 
2
2
[ '(t )]  [ '(t )]
|  '(t ) ''(t )   ''(t ) '(t ) |

(|  '(t ) |2  | '(t ) |2 )3/2
Кривизна плоской кривой
Пример. Найти кривизну окружности
( x  a) 2  ( y  b) 2  R 2
Параметрическое уравнение
R
t
 x  a  R cos t ,

 y  b  R sin t ,
0  t  2 .

Кривизна плоской кривой
|  ' (t ) ' ' (t )   ' ' (t ) ' (t ) |
k
(|  ' (t ) |2  |  ' (t ) |2 )3 / 2
 (t )  a  R cos t ,  (t )  b  R sin t
 ' (t )   R sin t ,  ' (t )  R cos t
 ' ' (t )   R cos t ,  ' (t )  R sin t
 ' (t ) ' ' (t )   ' ' (t ) ' (t )  ( R sin t )( R sin t )  ( R cos t )( R cos t )   R 2
|  ' (t ) |2  | ' (t ) |2  R 2 sin 2 t  R 2 cos 2 t  R 2
R2
R2 1
k  2 3/ 2  3 
(R )
R
R
Кривизна плоской кривой
Часто представляется удобным приближенно заменять кривую
вблизи рассматриваемой точки – окружностью, имеющую ту же
кривизну, что и кривая в данной точке.
Кругом кривизны кривой в данной точке M называется круг,
который
1) касается кривой в точке M;
2) направлен выпуклостью вблизи этой точки в ту же сторону, что
и кривая;
3) имеет ту же кривизну, что и кривая в точке M.
Центр круга кривизны называется центром кривизны, а радиус
этого круга – радиусом кривизны (в данной точке). Для радиуса
кривизны, очевидно, имеем формулу
1
R
k
(k  кривизна кривой )
Кривизна плоской кривой
Если кривая задана в параметрической форме
 x   (t ),

 y   (t ),
то координаты центра кривизны кривой в точке (x,y) равны

[ ' (t )]2  [ ' (t )]2
 ' (t ),
ξ  x 
 ' (t ) ' ' (t )   ' ' (t ) ' (t )


2
2
[

'
(
t
)]

[

'
(
t
)]
  y 
  ' (t ).

 ' (t ) ' ' (t )   ' ' (t ) ' (t )
Кривизна плоской кривой
Если кривая задана как график явной функции
y  f (x),
то параметрическое уравнение этой кривой имеет вид
x  t,

 y  f (t ).
Задача. Показать, что кривизна такой кривой
f ' ' ( x)
k
,
2 3/ 2
(1  [ f ' ( x)] )
а координаты центра кривизны
1  [ f ' ( x)]2
1  [ f ' ( x)]2
ξ  x
f ' ( x),   y 
.
f ' ' ( x)
f ' ' ( x)
Эволюта плоской кривой
Геометрическое множество центров кривизны данной кривой
называется ее эволютой. Сама кривая по отношению к своей
эволюте называется эвольвентой.
Пример. Найти эволюту параболы y2=2px.
Дифференцируя уравнение, находим
2 yy '  2 p; yy '  p,
( y ' ) 2  yy ' '  0; yy ' '  ( y ' ) 2 ; y 3 y ' '  ( yy ' ) 2 ; y 3 y ' '   p 2 .
Координаты центра кривизны
1  [ y ' ]2
(1  [ y ' ]2 ) y 2
y2  p2
2 px  p 2
3y2
ξ  x
y'  x 
yy ' ( x)  x 
 x
 3x  p 
 p,
y' '
y' ' y 3
p
p
2p
1  [ y ' ]2
(1  [ y ' ]2 ) y 2
y2  p2
y2
  y
 y
y  y
y 2.
y' '
y' ' y 3
p2
p
Эволюта плоской кривой
Из полученных уравнений
3y2
y2
ξ
 p,    2 .
2p
p
Исключаем y и получаем уравнение эволюты
2 
8
(ξ  p ) 3
27 p
(полукубическая парабола)
Метод итераций (последовательных приближений)
x   ( x)
Замечание.
f ( x )  0  x  x  cf ( x )  x   ( x ) ( ( x )  x  cf ( x ))
x1   ( x0 )
x2   ( x1 )

xn   ( xn 1 )

Метод итераций
Принцип сжимающих отображений
Пусть выполнены следующие условия
(1) x  [a, b]  ( x )  [a, b],
(2) q  (0,1) x, y  [a, b] |  ( x )   ( y ) | q | x  y | .
Тогда на отрезке [a,b] существует и притом единственное
решение уравнения
x   ( x ).
При этом метод итераций для x0∊[a,b] дает последовательность,
сходящуюся к решению этого уравнения. Более того
qn
| xn  x |
|  ( x0 )  x0 | .
1 q
Метод итераций
Доказательство. В силу условия (1) последовательность итераций
определена. Покажем, что она фундаментальна.
Лемма. При m≥n
| xm  xn | q n | xm n  x0 |
В самом деле
| xm  xn ||  ( xm1 )   ( xn 1 ) | q | xm1  xn 1 |
Применяя при m≥n полученное неравенство n раз, получаем
| xm  xn | q | xm1  xn 1 | q 2 | xm2  xn 2 | ...  q n | xmn  x0 |
Следствие:
| xn 1  xn | q n | x1  x0 |
Метод итераций
Оценим, теперь, величину
| xk  x0 || ( xk  xk 1 )  ( xk 1  xk 2 )  ...  ( x1  x0 ) |
 q k 1 | x1  x0 |  q k 2 | x1  x0 | ... | x1  x0 |
k
1

q
| x1  x0 |
k 1
k 2
 ( q  q  ...  1) | x1  x0 |
| x1  x0 |
.
1 q
1 q
Итак, мы имеем два неравенства
| x1  x0 |
| xm  xn | q | xmn  x0 |, | xk  x0 |
,
1 q
n
Из которых следует, что при m≥n
| x1  x0 |
| xm  xn | q
1 q
n
Метод итераций
| x1  x0 |
| xm  xn | q
(m  n)
1 q
n
ε0
| x1  x0 |
n | x1  x0 |
lim q
 0  N n  N q

n 
1 q
1 q
n

n  N , m  n | xm  xn | 

m, n  N | xm  xn | 
Метод итераций
x  lim xn
n 
(1) a  xn  b  x  [a, b]
(2) 0 |  ( xn )   ( x ) | q | xn  x |   ( xn )   ( x)
(3) xn   ( xn 1 )  x   ( x )
| x1  x0 |
n | x1  x0 |
| xm  xn | q
, m    | x  xn | q
1 q
1 q
| x  xn || xn  x |, | x1  x0 ||  ( x0 )  x0 |
n

qn
| xn  x |
|  ( x0 )  x0 |
1 q
Метод итераций
Единственность решения.
x   ( x ), y   ( y )
| x  y ||  ( x )   ( y ) | q | x  y |
(1  q) | x  y | 0
| x  y | 0
x y
Иоганн Кеплер
Немецкий математик, астроном и оптик,
27.12.1571 – 15.11.1630 первооткрыватель законов движения планет
Солнечной системы.
В 1591 поступил в университет в Тюбингене, в
1594 приглашен для чтения лекций по
математике в университет города Граца
(Австрия).
На протяжении нескольких лет Кеплер в
результате тщательного анализа приходит к
выводу, что траектория движения Марса
представляет собой не круг, а эллипс, в одном из
фокусов
которого
находится
Солнце
—
положение, известное сегодня как первый закон
Кеплера.
Дальнейший анализ привёл ко второму закону: радиус-вектор,
соединяющий планету и Солнце, в равное время описывает равные
площади. Это означало, что чем дальше планета от Солнца, тем
медленнее она движется.
Иоганн Кеплер
В 1612 году Кеплер переезжает в Линц, где прожил 14 лет. За ним
сохранена должность придворного математика и астронома, но в деле
оплаты новый император ничем не лучше старого. Некоторый доход
приносят преподавание математики и гороскопы.
Продолжая астрономические исследования, Кеплер в 1618 году
открывает третий закон: отношение куба среднего удаления планеты от
Солнца к квадрату периода обращения её вокруг Солнца есть величина
постоянная для всех планет: a³/T² = const. Этот результат Кеплер
публикует в завершающей книге «Гармония мира», причём применяет его
уже не только к Марсу, но и ко всем прочим планетам, включая,
естественно, и Землю.
В 1626 году в ходе Тридцатилетней войны Линц осаждён и вскоре
захвачен. Начинаются грабежи и пожары. Кеплер переезжает в Ульм.
В 1630 году отправляется к императору в Регенсбург, чтобы получить
хотя бы часть жалованья. По дороге сильно простужается и вскоре
умирает.
Законы планетной кинематики, открытые Кеплером, послужили позже
Ньютону основой для создания теории тяготения. Ньютон математически
доказал, что все законы Кеплера являются следствиями закона тяготения.
Эллипс
y
r1  r2  2a
b
b  a 2  c2
r1
c
r2
c
x
a
x2 y2
 2  1 ( a  b)
2
a
b
a  большая полуось
b  малая полуось
x2  y 2  a2
c
ε   эксцентриситет
a
Уравнение Кеплера
  истинная аномалия
x  эксцентрическая аномалия
T  период обращения
μ  m1  m2
x
апоцентр
линия апсид

фокус
перицентр
2


T
g
a3
(среднее движение)
t  время движения от перицентра
m  t  средняя аномалия
m  x  εsin x
Метод итераций (пример)
Уравнение Кеплера
x  m  ε sin x (0  ε  1)
 ( x )  m  ε sin x
[a , b]  [m  1, m  1]
 '( x )  ε cos x  |  '( x ) | ε
| ( x )   ( y )|=| '(ξ)( x  y )|  ε|( x  y )|
Таким образом, итерации
xn  m  ε sin xn 1
сходятся к единственному решению этого уравнения.
Метод итераций (пример)
Оценка погрешности:
1619
εn
| xn  x |
|  ( x0 )  x0 | .
1 ε
x  2  0,1sin x (с точностью до 0,001)
(0,1)n
m  2 ε  0,1 d 
|  ( x0 )  x0 |
0,9
x0  2,
d  0,1
x1  2,09093, d  0,01
x2  2,08678, d  0,001
x3  2,08698, d  0,0001
Ответ:
x  2,087
Дистанционный курс высшей математики
НИЯУ МИФИ
Математический анализ.
Приближенные методы
решения уравнений.
Лекция 13
завершена.
Спасибо за внимание!
Тема следующей лекции:
Обзорная лекция.
Лекция состоится в четверг 18 декабря
В 10:00 по Московскому времени.