Тема3-1_Теория ротоанемометров

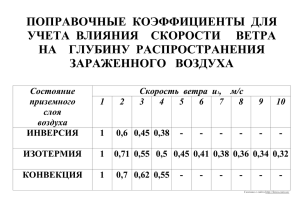
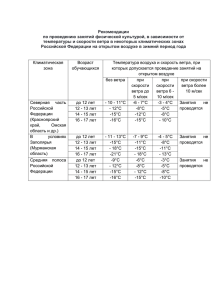
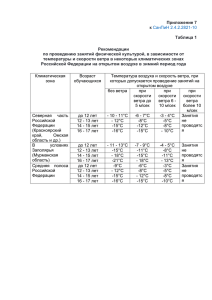
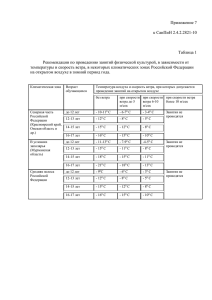
Тема 3.
ИЗМЕРЕНИЕ ПАРАМЕТРОВ
ВОЗДУШНЫХ ПОТОКОВ
СОДЕРЖАНИЕ ТЕМЫ
3.1. Теория ротоанемометров
3.2. Индукционные ротоанемометры
3.3. Импульсные (контактные) ротоанемометры
3.4. Акустические анемометры
3.5. Лазерный доплеровский измеритель скорости
ветра
3.6. Измерение направления ветра. Измерители
направления ветра с сельсинной передачей
3.1. Теория ротоанемометров.
Ротоанемометры – приборы для измерения скорости ветра,
имеющие вращающийся винт или чашечную вертушку.
1
4
2
3
Рис. 3.1.1. Чашечная вертушка
Винт или вертушка преобразуют скорость ветра в угловую
скорость вращения.
Докажем, что угловая скорость вращения вертушки однозначно
связана со скоростью ветра.
3.1. Теория ротоанемометров.
1)
Рассмотрим силы,
действующие на чашки.
V
F1
3)
V
F3
Поскольку ветер
обтекает 3-ю чашку, то:
F1  F3
Рис. 3.1.2. Обдувание чашек ветром.
3.1. Теория ротоанемометров.
Силы, действующие на 2-ю и 4-ю чашку, подобны силам,
действующим на крыло самолета. Они невелики по сравнению
с F1 и F3.
F4
F2
Рис. 3.1.3. Обдувание ветром второй и четвертой чашки.
3.1. Теория ротоанемометров.
В результате вертушка начинает вращаться.
Рис. 3.1.4. Вращение вертушки.
Если ветер меняет направление, то вертушка все равно вращается
в ту же сторону!
Чашечная вертушка не чувствительна к направлению ветра.
3.1. Теория ротоанемометров.
При вращении вертушки 1-я чашка движется по потоку, сила
F1 уменьшается. Третья чашка движется против потока, сила
F3 возрастает.
F1
v
F3
Когда наступает равенство моментов сил, угловая скорость
вертушки становится постоянной. Докажем, что эта скорость
связана со скоростью ветра.
3.1. Теория ротоанемометров.
Уравнение движение вращающейся вертушки:
d
i M i  K  d
Mi
- моменты сил, действующих на чашки,
K - момент инерции всей вертушки,

- угловая скорость вращения вертушки.
(3.1.1)
3.1. Теория ротоанемометров.
 Mi  K 
Предположим:
i
d
d
1. Сумма сил, действующих на вертушку, не зависит от положения
вертушки.
2. Силы F2 и F4 пренебрежимо малы.
3. Сила трения пренебрежимо мала по сравнению с F1 и F3.
4. Скорость вращения стабилизировалась, т.е.
d
0 .
d
Тогда:
F1
M1  M 3  0
F4
R
Или:
R  p1  R  p3  0
где Рi – аэродинамическое давление на чашку.
F2
F3
3.1. Теория ротоанемометров.
R  p1  R  p3  0
Известно, что:
1
p   C    S  (V ) 2
2
С – коэффициент аэродинамического сопротивления чашки,
ρ – плотность воздуха,
S – площадь проекции чашки на плоскость, перпендикулярную
потоку ветра,
V’ – скорость ветра относительно чашки.
1
1
C1    S  (V  U )2   C3    S  (V  U ) 2
2
2
U – линейная скорость движения чашки.
(3.1.2)
3.1. Теория ротоанемометров.
1
1
C1    S  (V  U )2   C3    S  (V  U ) 2
2
2
2
C1  (V  U ) 2  C3  (V  U ) 2 : C3U
2
C1  V
 V

  1    1
C3  U   U 
C1
4
C3
Установлено, что:
Тогда, обозначив
2
V
  , имеем:
U
4    1    1
2
2
(3.1.3)
3.1. Теория ротоанемометров.
Это квадратное уравнение имеет два корня:
4    1    1
2
Поскольку
V
   1 , то:
U
2

 3
1  3
2 
1
3
  const
Учтем соотношение между угловой (Ω) и линейной (U)
скоростью вертушки:
U  R
Тогда:
V

 R
(3.1.4)
3.1. Теория ротоанемометров.
Построим график Ω(V):
Ω
V*
V
Рис. 3.1.5. Зависимость угловой скорости вращения
вертушки от скорости ветра. V* - пороговая скорость.
Наличие трения приводит к нелинейной зависимости при малой
V. При скорости V<V* вертушка вообще не вращается.
Скорость V*, при которой вертушка начинает вращаться,
называется пороговой скоростью анемометра.
3.1. Теория ротоанемометров.
Способы уменьшения пороговой скорости.
1. Уменьшать силу трения на оси вертушки.
2. Пользоваться легкими небольшими вертушками.
3. Анемометры с винтом имеют меньшую пороговую
скорость.
3.1. Теория ротоанемометров.
Самые легкие вертушки
(например, у анемометра
АСО-3) имеют пороговую
скорость 0,1 – 0,2 м/c.
Рис. 3.1.6. Анемометр с винтом.
3.1. Теория ротоанемометров.

Определим чувствительность вертушки:
d
1

S
dV   R
(3.1.5)
Для увеличения чувствительности вертушки ее радиус
следует делать малым.
V
 R
3.1. Теория ротоанемометров.
Теперь рассмотрим случай неустановившейся угловой скорости.
Пусть угловая скорость вращения вертушки была равна ω0.
Скорость ветра изменилась скачком. Новая угловая скорость
вертушки – Ω. Но она устанавливается не сразу.
 Mi  K 
i
d
d
Из аэродинамики:
 
i M i  kV  
2
k
– постоянный размерный коэффициент.
(3.1.6)
3.1. Теория ротоанемометров.
 Mi  K 
i
Или:
Разделим
переменные:
И проинтегрируем:
d
d
d
2  
K
 kV
d

d
2  
K
 kV
d

d
k V 2

d
 
K 


d
k V 2
     0 K   d
0
 M i  kV 2 
i
 

3.1. Теория ротоанемометров.


d
k V 2
     0 K   d
0
 
k V 2
ln


0  
K 
Откуда:
    ( 0)  e
Преобразуем:

k V 2

K 

    (0 )  e
Обозначим
V 
K 
k V
K 
 L . Тогда:
k V
    ( 0 )  e

V 
L
(3.1.7)
3.1. Теория ротоанемометров.
    ( 0 )  e
При
   
K 
L
k V
V 
L
.
Скорость изменения ω зависит от L.
Назовем: L – путь синхронизации.
При L = V :

  
L  м
L  const.
0  
e
Путь синхронизации – это путь, проходимый воздушным
потоком, за время, в течение которого разность между угловой
скоростью вращения вертушки (ω) и установившейся угловой
скоростью (Ω) уменьшится в е раз.
3.1. Теория ротоанемометров.
Учтем:

Тогда:
Но:
V
 R
K 
K
L

k V
k  R 
K  nmR2
n – количество чашек,
m – масса одной чашки.
Тогда:
K
nmR
nmR2
L


k  R  k  R  k 
(3.1.8)
Значит, легкая (c малой m), маленькая (с малым R) вертушка
обладает малым путем синхронизации.
3.1. Теория ротоанемометров.
Можно ввести время синхронизации * - время, в течение
которого разность угловых скоростей уменьшается в е раз.
Но:
L
 *   const
V
V

*
(?!)
Чем больше скорость ветра, тем быстрее ее воспринимает
вертушка!
3.1. Теория ротоанемометров.
Покажем это на графике.
ω
Ω2
 2  0
e
2
Ω1
1
ω0
2 *
1 *

Рис. 3.1.7. Изменение угловой скорости вращения
вертушки при малой (1) и при большой (2) скорости ветра.
3.1. Теория ротоанемометров.
Рассмотрим реакцию вертушки на прямоугольные флуктуации
скорости ветра.
V
Показания анемометра
Скорость ветра
Vанем.
Vист.

Рис. 3.1.8. Показания анемометра при порывистом ветре.
Ротоанемометр завышает среднюю скорость ветра.
3.1. Теория ротоанемометров.
Ошибка в определении средней скорости тем больше, тем
больше путь синхронизации анемометра.
Существующие ротоанемометры имеют путь синхронизации от
нескольких метров до десятков метров. Его величина указывается
в паспорте прибора и является мерой инерции анемометра.