Лекция №8 и №9
реклама

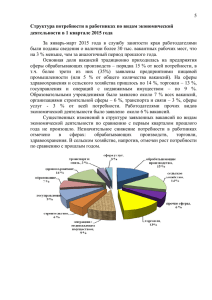
Диффузия в кристаллах лекция 1 Точечные дефекты 1 5,6 2 Соединение АВ 3,4 1- вакансия в подрешётке А 2 - вакансия в подрешётке В 3 - межузельный атом А 4 - межузельный атом В 5 - примесный атом замещения 6 - примесный атом внедрения 7,8 – антиструктурные дефекты 7,8 Собственные точечные дефекты Собственные точечные дефекты – вакансии и межузельные атомы. Причины образования Тепловые дефекты Обмен кристалла теплом с внешней средой приводит к образованию вакансий и межузельных атомов в результате тепловых флуктуаций. При Т=0 К тепловых дефектов нет. Максимальная концентрация тепловых дефектов вблизи температуры плавления (С ~ 10-5 – 10-4 ). Дефекты нестехиометрии и дефекты, обусловленные присутствием примесных атомов. Обмен кристалла веществом с внешней средой приводит к изменению химического состава кристалла. Отклонение химического состава от стехиометрического приводит к образованию вакансий и межузельных атомов - дефектов нестехиометрии. Присутствие в кристалле примесных атомов также может вызывать образование вакансий и межузельных атомов. Тепловые точечные дефекты Механизмы образования тепловых точечных дефектов Беспорядок по Френкелю – образование вакансии и межузельного атома. Беспорядок по Шоттки – образование вакансий. Ионные соединения По Шоттки + - - + + - - + + - + + + - + + - + + + - По Френкелю в катионной подрешётке в анионной подрешётке - + + - + + - + + + + - + - + - + + - + + - - + - - + - + + + - + - + + - + + + + - + - + + - + + - + - + + - + + - - + + - + + - + Эффективный заряд – заряд дефекта по отношению к заряду структурного элемента бездефектного кристалла на месте которого этот дефект локализован. В идеальном кристалле каждый узел и междоузлие имеют нулевой заряд. Эффективный заряд вакансии равен по величине и противоположен по знаку заряду покинувшего узел иона. Эффективный заряд межузельного иона совпадает по знаку и по величине с зарядом вошедшего в междоузлие иона. Различные варианты нестехиометрии (на примере оксидов металлов) Недостаток металла – внедрение кислорода. M1-xO Образование катионных вакансий ½ O2 ↔ OxO + V’’M + 2 h● Примеры оксидов: Cu2O, CoO, NiO, TiO, NbO. MO1+x Образование междоузельного кислорода ½ O2 ↔ O’’i + 2 h● Примеры оксидов: UO2, CeO2, ThO2, La2O3. Избыток металла – выделение кислорода. MO1-x Образование анионных вакансий «O» ↔ ½ O2 + V●●O + 2 e’ Примеры оксидов: TiO, TiO2, CuO, NbO, Nb2O5. M1+xO Образование междоузельного металла «O» ↔ ½ O2 + M●●i + 2 e’ Примеры оксидов: CdO, ZnO, Fe2O3. Образование катионных вакансий O2 ↔ 2OxO + 2V’’M + 4 h● Примеры оксидов: CoO, NiO, TiO, NbO. O O O O M O M O M O M M O M O M O M O O M O M O M O M M O M O M O M O O M O M O M O M O O Образование межузельного кислорода O2 ↔ 2O’’i + 4 h● Примеры оксидов: UO2, CeO2, ThO2, La2O3. O O M O O M O O O O M O M O M O M O M O M O M O M O Образование анионных вакансий «O» ↔ O2 + 2V●●O + 4 e’ Примеры оксидов: TiO, TiO2, CuO, NbO, Nb2O5. O O O M O M O M O M M O M O M O M O O M O M O M O M M O M O M O M O O M O M O M O M Образование межузельного металла «O» ↔ O2 + 2M●●i + 4 e’ Примеры оксидов: CdO, ZnO, Fe2O3. O O O M O M O M M O M O M O M O M O M O M M O M O M O Основные механизмы диффузии в кристаллах Б A В А – вакансионный (наиболее распространенный ) Б – прямой межузельный ( пример: С в Fe) В – непрямой межузельный ( пример: Аg● Ag в AgBr) Diffusio (лат.) – распространение. 1855 – А. Фик получил закон, связывающий поток частиц с градиентом концентрации при исследовании растворов соли в воде. dC j D dx • D – коэффициент диффузии . • Характерные величины, см2/c: • Газы - 10 -1 • Жидкости 10-5 • Твёрдые вещества < 10-8 Первое сообщение о диффузии в твёрдом теле – 1896 Р. Аустен, диффузионная пара Pb+Au, 200 oC, 10 дней. s 1 J C s 6 1 1 dC J (C C ) s s (C s ) 6 6 dx 1 dC dC J J J s 2 D 6 dx dx 1 D s 2 6 Хаотическая диффузия Одномерный случай - равная вероятность прыжка вправо и влево. s - длина прыжка. Позиция после первого прыжка x1 = 0 ± s. x1 0 Средняя позиция 2 2 Средняя квадратичная позиция x1 (0 s) s 2 Позиция после второго прыжка x2 = x1 ± s. 2 2 2 2 2 2 2 Средняя квадратичная позиция x2 ( x1 s ) ( x1 2 x1 s s ) x1 s 2s Средняя квадратичная позиция после N прыжков xN2 N s 2 t s 2 6 D t Диффузионный путь x x s N s t 6D t 2 Броуновское движение Броун, 1827 Соотношение Смолуховского-Энштейна R T x t 6D t 3 r N a 2 А. Энштейн «О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты» Annalen der Physik, 1905 Выражения для коэффициента диффузии. Вакансионный механизм DHm Коэффициент диффузии вакансии DS DH m 1 1 DV s 2 s 2 0 exp( m ) exp( ) 6 6 k k T DH m V Do exp( ) k T о - частота колебаний атомов (о =1013 с-1 выше температуры Дебая); s– длина прыжка (например, s a / 2 для ГЦК решётки , где а - параметр ячейки). Коэффициент диффузии атома DH D Da DV V f Do exp( ) k T [V] – концентрация вакансий; f – корреляционный фактор (определяет неравноценность позиций в решётке для прыжков атома). f = 1-2/Z. 1) Металлы DH Ш VMX exp(DS Ш / k ) exp( ) k T DS DS Ш DH m DH Ш DH D 1 DV s 2 0 exp( m ) exp( ) Do exp( ) 6 k k T k T DH D DH m DH Ш 2) Ионные кристаллы АХ V 'A V X exp(DS / 2k ) exp( DH Ш ) 2k T 2DSm DS Ш 2DH m DH Ш DH D 1 DV s 2 0 exp( ) exp( ) Do exp( ) 6 2k 2k T k T DH Ш DH D DH m 2 Выражения для коэффициента диффузии. Межузельный механизм DHm DSm DH m 1 2 Di s 0 Vi exp( ) exp( ) 6 k k T [Vi] – концентрация незанятых междоузлий. Пример: атомы внедрения в металлах (H, C, B в Ta, Mo, V, Fe). Энтальпия активации дифузии металл DHm, кДж/моль DHD, кДж/моль Tпл, К Al 60 130 933 Ag 90 180 1233 Cu 100 210 1356 W 330 660 3653 DH D D Do exp( ) k T ОЦК, ГЦК, ГПУ металлы, галогениды щелочных металлов, оксиды со структурой NaCl (CaO, MgO, CoO, FeO, NiO и т.д.), карбиды и бориды металлов D010-2 – 1 см2/c, DHD= 15-20 RTпл, D(Tпл) = 10-10 – 10-8 см2/с Вещества со структурой алмаза D0104 см2/c, DHD= 35 RTпл, D(Tпл) = 10-16 см2/с Направленная диффузия D j C k T x q 0 k T ln C q - электрохимический потенциал 0 1 C k T q x x C x x D 0 C D j C D C qE kT x x kT - суммарный поток Диффузия в градиенте концентрации – первый закон Фика o 0, E 0 x dC j D dx Pb Au Диффузия в градиенте давления – эффект Горского растяжение C 0, E 0 x D P j C kT x сжатие P растяжение сжатие Ω – атомный объём h h C h Диффузия в электрическом поле – ионная проводимость o C 0, 0 x x D j C qE kT -закон Ома, σ – удельная электропроводность i q j E (Ом-1·см-1) D 2 C q C q kT D q - подвижность частицы- соотношение kT Нерста-Энштейна N i i ti i - число переноса N i i В нестехиометрических соединениях преобладает электронная проводимость (по e’ или h), а в стехиометрических – ионная проводимость (вакансии или междоузельные атомы). Температурная зависимость ионной удельной электропроводности имеет вид: DH m o n exp( ) k T Из измерений ионной проводимости, можно получить информацию о концентрации дефектов и их подвижности. Диффузия в кристаллах лекция 2 Участок 1 - собственная проводимость. При температурах близких к температуре плавления в кристалле преобладают тепловые дефекты. «О» ↔ V′Na + V●Cl В этом случае концентрация носителей заряда – катионных вакансий определяется выражением DH Ш ) V 'Na exp(DS / 2k ) exp( 2k T и проводимость равна: DH m (DH m DH Ш / 2) ) 'o exp( k T k T Тангенс угла наклона первого участка будет равен –(∆Hm +∆HШ/2)/R. Участок 2 - примесная проводимость. Наличие CaCl2 приводит к образованию катионных вакансий CaCl2 → Ca●Na + V’Na + 2 ClxCl При понижении температуры количество вакансий, образовавшихся в результате введения примесных атомов, может превысить концетрацию собственных тепловых точечных дефектов. В этом случае [n]=[Ca2+] и o V 'Na exp( o Ca Na exp( DH m ) k T Тангенс угла наклона второго участка будет равен –∆Hm /R. Эффект Коха - Вагнера В AgBr ионный перенос происходит за счёт диффузии катионов. Катионы могут диффундировать как по вакансионному, так межузельному механизму. Каждый из этих диффузионных процессов вносит свой вклад в проводимость кристалла. q ( Ag i i V ' Ag V ) Зависимость относительной ионной проводимости в кристаллах AgBr с увеличением концентрации введенной примеси CdBr2 при постоянной температуре сначала убывает, достигает минимума, а затем начинает увеличиваться. Такая необычная зависимость ионной проводимости от концентрации примесных атомов называется эффектом Коха-Вагнера. Попытаемся объяснить наблюдаемую зависимость. Подвижность межузельного серебра выше подвижности катионной вакансии (χi > χ V). Поэтому в чистом веществе больший вклад в проводимость вносит диффузия межузельного серебра. Замещение ионов серебра ионами кадмия приводит к образованию вакансий серебра. CdCl2 → Cd●Ag + V’Ag + 2 ClxCl При этом концентрация межузельного серебра уменьшается. Начальное падение проводимости связано с тем, что увеличение вклада в проводимость связанное с повышением концентрации катионных вакансий не может компенсировать уменьшение проводимости, связанное с уменьшением концентрации межузельного серебра. Падение будет происходить до тех пор, пока вклад вакансионного потока в общую проводимость не станет доминирующим. Дальнейшее повышение концентрации примеси приводит к увеличению потока вакансий и общему росту проводимости. 1914 – Тубанд и Лоренц обнаружили резкое увеличение проводимости после β→α превращения в AgI. Tβ→α=146 oC Фазовый переход в AgI β-фаза P63mc α-фаза Im3m wyck x/a y/b z/c S.O.F. I 2a 0. 0. 0. 1. Ag1 12 d 0.25 0. 0.5 0.0967 Ag2 24 h 0.385(7) 0.385(7) 0. 0.035 Cooper M. J., Sakata M. Acta Crystallographica A, 35(1979) 989-991 Эффекты, обусловленные диффузией Диффузионная пара. Различие в диффузионной подвижности атомов приводит к накоплению вакансий в веществе с меньшей подвижностью. JA > JB Эффект Киркендаля – перемещение границы раздела (пример:медь-латунь) ∆V/V=0 Эффект Френкеля – образование пор (пример:никель-медь) ∆V/V>0 Диффузия и химические реакции. Реакции твёрдое + газ. Окисление металлов катионы ионы кислорода электроны металл оксид D j C k T x iионов qi jионов qe jэлектронов iэлектронов Dк D к dx jион (Cк dt k T Dx DО DО CО ) k T Dx Окисление определяется диффузией металла к внешней поверхности. А. Оксид дефектен по Шоттки tэ~1, DO<<DM NiO, FeO, Cu2O KV M ½ O2 ↔ OxO + V’’M + 2 h● оксид V’’M h● V’’M + 2h ● +Mx x Me ↔M M + металл VxMe D[V ''M ] dx 1 jк DV k dt x x x 2 2k t [V ''M ] [h ]2 KV M pO1/22 KVM 13 16 1 [V ''M ] [h ] ( ) pO2 2 4 1 1 K M 13 dx 1 DV ( ) ( p1O6 2 p2O6 2 ) dt 4 x p1O2 p2O2 1 K M 13 dx 1 DV ( ) p1O6 2 dt 4 x 1 K M 13 k DV ( ) p1O6 2 4 Суммарное уравнение: ½ O2 + MxMe ↔ OxO + MxM + VxMe Скорость окисления определяется диффузией катионных вакансий от внешней поверхности. В результате окисления в металле накапливаются вакансии. Б. Оксид дефектен по Френкелю в катионной подрешётке tэ~1, DO<<DM ZnO, CdO ½ O2 + M ● ● i + 2e’ ↔ OxO + MxM оксид M ●●i e’ MxMe ↔M ● ● i + VxMe + 2e’ металл Суммарное уравнение: ½ O2 + MxMe ↔ OxO + MxM + VxMe Скорость окисления определяется диффузией межузельных катионов к внешней поверхности. В результате окисления в металле накапливаются вакансии. Окисление определяется диффузией кислорода. tэ~1, DO>>DM ZrO2, CeO2, ThO2 ½ O2 + V ● ● O + 2e’ ↔ OxO + MxM оксид V ●● O e’ MxMe ↔MxM + V ● ● O + 2e’ металл Суммарное уравнение: ½ O2 + MxMe ↔ OxO + MxM Скорость окисления определяется диффузией анионных вакансий к внешней поверхности. Диффузия и химические реакции. Реакции твёрдое +твёрдое. AO + B2O3 ↔AB2O4 1) Противоположная диффузия катионов DA, DB >>DO 3 A2+ AO B2O3 2 B3+ AB2O4 3A2+ + 4B2O3 ↔ 3 AB2O4 + 2 B3+ 2 B3+ + 4 AO ↔AB2O4 + 3A2+ 2) Сопряженная диффузия A2+ и O2- DO, DA >>DB A2+ AO O2- B2O3 AB2O4 A2+ + O2- + B2O3 ↔ AB2O4 Диффузия и химические реакции. Реакции твёрдое +твёрдое. AO + B2O3 ↔AB2O4 3) Сопряженная диффузия B3+ и O2- DB, DO >>DA 3 O2AO 2 B3+ AB2O4 AO + 2B3++ + 3O2- ↔ AB2O4 B2O3 Диффузия и химические реакции. Реакции твёрдое +твёрдое. МgO + Fe2O3 ↔MgFe2O4 T=1000 oC, PO2=1 атм 1 3 3 Mg2+ 2 Fe3+ MgO Fe2O3 MgFe2O4 2 Fe3+ + 4 MgO ↔MgFe2O4 + 3Mg2+ 3Mg2+ + 4Fe2O3 ↔ 3 MgFe2O4 + 2 Fe3+ Диффузия и химические реакции. Реакции твёрдое +твёрдое. МgO + Fe2O3 ↔MgFe2O4 T=1000 oC, PO2<1 атм O2 «О» ↔3/2O2 + 6e’ + 2Fe3+ e’ Fe3+ MgO Fe2O3 MgFe2O4 2 Fe3+ + MgO + 3/2 O2 + 6 e’↔MgFe2O4